Решения задач средствами пакета Mathcad
Тема 1. Решение алгебраических и трансцендентных уравнений
Решение задачи на практических занятиях
Задание.Выбрать нелинейное уравнение из табл. и затем:
· отделить корень уравнения.
· проверить выполнение условий сходимости (в методе итераций, в случае расходящегося процесса – сделать необходимые преобразования для обеспечения сходимости);
· выбрать начальное приближение
·
1. Отделение корня уравнения.
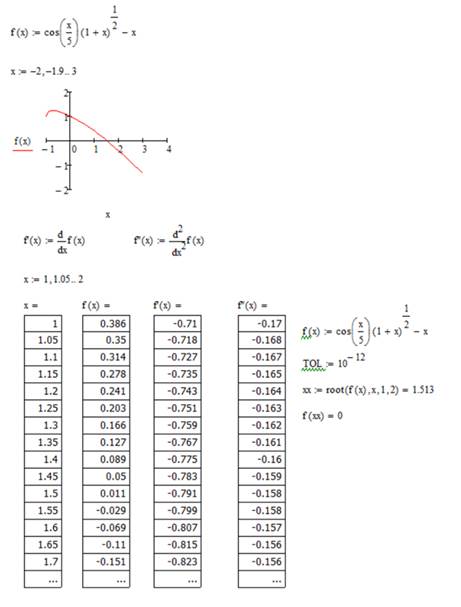
2. Уточнение корня уравнения
Результаты расчета для трех итераций (метод половинного деления).

Результаты расчета для трех итераций (метод Ньютона).
«Ручной расчет» трех итераций
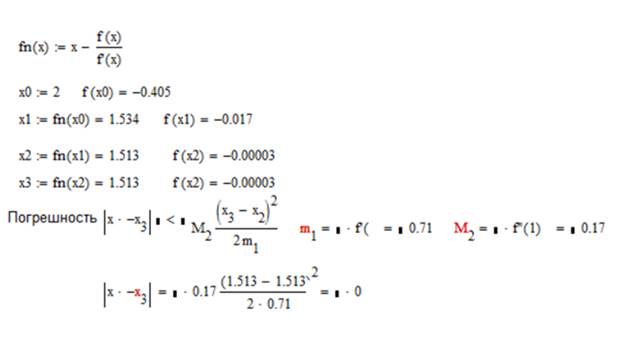 |
Представим вычисления в виде следующей табл. 1.2-2b.
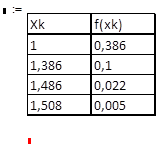
Домашняя работа
Результаты расчета для трех итераций (метод итераций).
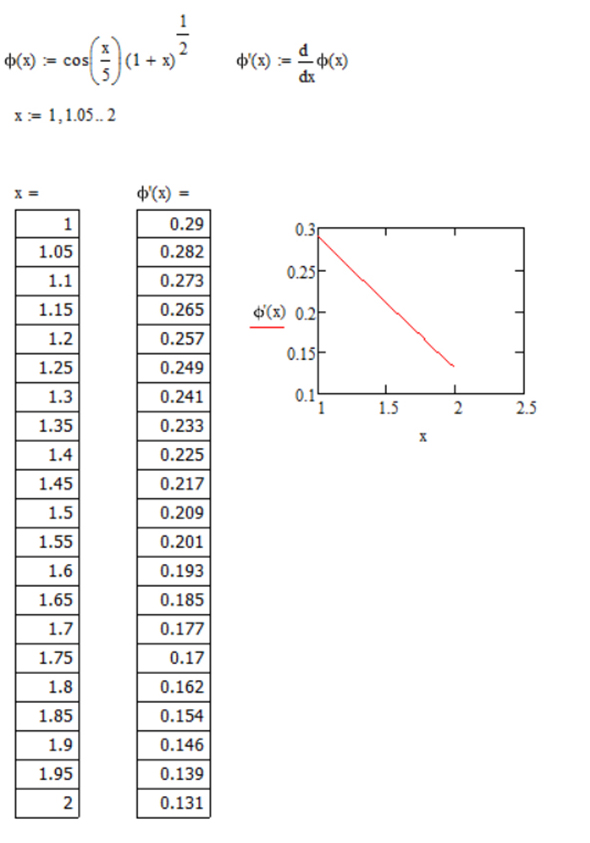
Для сходимости метода необходимо представить уравнение f(x)=0 в виде x=φ(x). Для сходимости метода необходимо, чтобы первая производная от функции φ(x) была по модулю <1.
Приведем уравнение f(x)=0к виду x = 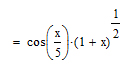 и проведем исследование.
и проведем исследование.
 |
Выберем начальное значение (в методе итерацийx0– произвольное значение из отрезка [a;b]), например, x0=0, и с использованием итерационной функции 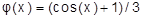 выполним три итерации.
выполним три итерации.
2. «Ручной расчет» трех итераций
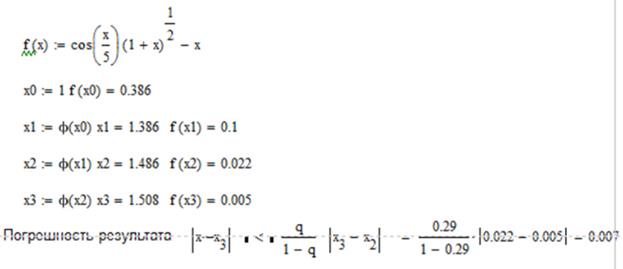 |
Тема 2. Технология вычисления интегралов в среде
Математических пакетов
Задание: вычислить интеграл заданными методами.
В домашней работе вычислить интеграл из своего индивидуального задания третьим методом (например, если в лабораторной работе использовались методы средних прямоугольников и трапеций, то использовать метод Симпсона и т.д.)
Решение задачи на практических занятиях
· определенный интеграл 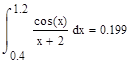
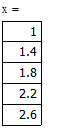
· шаг интегрирования h=1.4.
Вычисление определенного интеграла
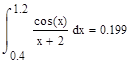
Получение таблицы значений подынтегральной функции
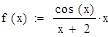
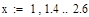
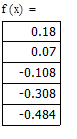
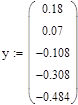
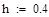
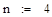
Интегрирование с использованием численных методов
Метод трапеций
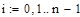
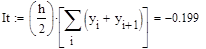
Метод Симпсона
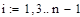
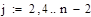
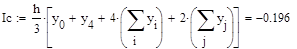
Домашняя работа
Метод средних прямоугольников
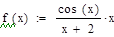
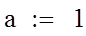
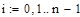
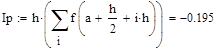
Тема 3. Технология решения задач одномерной
Оптимизации средствами математических
Пакетов
Задание.
· построить график функции f(x), выбрать отрезок, содержащий минимум, и проверить на нем условие унимодальности функции;
· Провести «ручной расчет» 3-х итераций по поиску минимума функции f(x) на отрезке [a;b], в соответствии с заданным методом.
В домашней работе вычислить минимум вторым (не использующимся в лабораторной работе) методом.
Решение задачи на практических занятиях
F(x)=sin(2*x)-x
Решения задач средствами пакета Mathcad
Отделение отрезка унимодальности 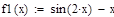 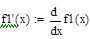 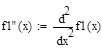 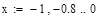 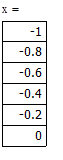 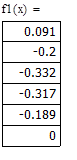 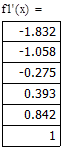 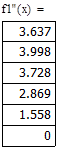 Первая производная не убывает, а вторая - положительна, следовательно, на отрезке [0;1] существует единственный минимум Первая производная не убывает, а вторая - положительна, следовательно, на отрезке [0;1] существует единственный минимум 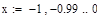 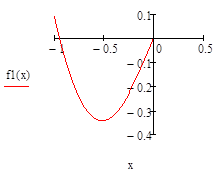 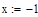 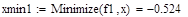 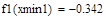 Вычисление координат точки минимума на отрезке [1;2] Вычисление координат точки минимума на отрезке [1;2] 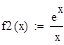 Построим график функции f2(x) на заданном отрезке Построим график функции f2(x) на заданном отрезке 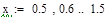 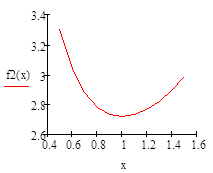 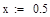 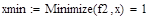 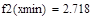 |
F(x)=sin(2*x)-x
| Метод дихотомии |
| F(x)=sin(2*x)-x |
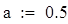 |
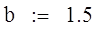 |
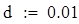 |
| 1 итерация |
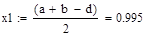 |
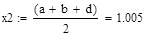 |
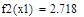 |
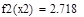 |
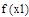 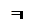 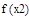 |
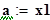 |
| после 1 итерации |
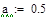 |
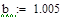 |
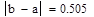 |
| 2 итерация |
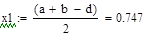
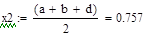
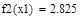
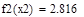
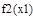 >
> 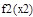
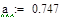
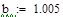
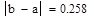
3 итерация
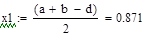
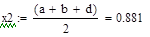
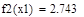
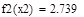
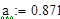
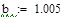
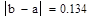
Таблица

Домашняя работа
Три итерации методом золотого сечения
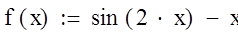
| Метод золотого сечения |
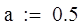 |
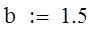
| 1 итерация |
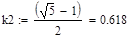 |
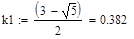 |
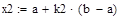 |
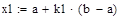 |
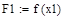 |
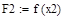 |
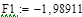 |
 |
 |
 |
 |
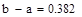 |
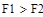 |
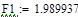 |
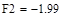 |
| 2 итерация |
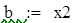 |
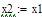 |
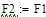 |
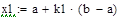 |
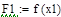 |
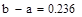 |
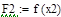 |
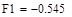 |
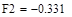 |
| 3 итерация |
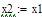 |
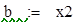 |
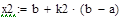 |
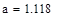 |
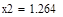 |
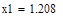 |
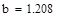 |
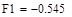 |
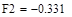 |
