Физическое моделирование движения жидкости

В данном разделе приведены уравнения движения реальной жидкости, получено описание процесса движения жидкости в безразмерном виде, установлены уравнения подобия для процессов движения жидкости, рассмотрены условия моделирования процессов движения жидкости.

3.1 Уравнения движения реальной жидкости

При омывании поверхности твердого тела текучей средой (жидкостью или газом), характер движения жидкости значительно влияет на конвективный теплообмен между жидкостью и телом. Также, характер движения жидкости может представлять самостоятельный интерес, например, в гидравлике.

Известно, что конвекция (т.е. движение жидкости) может быть вынужденной или свободной. При вынужденной конвекции объем жидкости приводится в движение за счет внешних поверхностных сил (давления, трения) приложенных на его границах, за счет предварительно сообщенной кинетической энергии (например, за счет работы вентилятора, насоса, ветра). Также вынужденным считается движение жидкости под действием однородного поля массовых сил (силы тяжести и др.). Свободная конвекция в рассматриваемом объеме жидкости возникает за счет неоднородности в нем массовых сил. Например, если жидкость с неоднородным распределением температуры, и как следствие, с неоднородным распределением плотности, находится в поле земного тяготения, может возникнуть свободное гравитационное движение.

Поле скоростей при вынужденном движении реальной жидкости, обладающей вязкостью, описывается уравнением Навье-Стокса:

(3.1)

где - поле скоростей в рассматриваемом объеме жидкости, причем , где w_x, w_y, w_z – компоненты вектора скорости на декартовы оси; r, р - плотность и давление жидкости; m - коэффициент динамической вязкости жидкости; - вектор ускорения свободного падения; Ñ– оператор градиента; Ѳ - оператор Лапласа.

Физический смысл уравнения (3.1) состоит в том, что произведение массы частицы жидкости единичного объема на ее ускорение обусловлено действием силы тяжести , силами давления , и силами вязкостного трения , действующими на данную частицу. Таким образом, уравнение (3.1) отражает второй закон Ньютона.

Полные производные , , можно записать в следующем виде:

(3.2)

где , , - частные производные компонентов скорости по времени. При стационарном течении жидкости эти производные равны нулю:

(3.3)

В развернутом виде уравнение (3.1), с учетом (3.2) и (3.3), при стационарном вынужденном движении жидкости распадается на три уравнения:

(3.4)

где g_x, g_y, g_z – проекции вектора ускорения силы тяжести на декартовы оси; n – коэффициент кинематической вязкости: n = m/r.

Свободное движение жидкости при гравитационной конвекции возникает, когда плотность жидкости изменятся с температурой. Зависимость плотности от температуры можно приближенно описать выражением:

(3.5)

где r, r₀ - плотность жидкости при температурах t и t₀; - избыточная температура; b - температурный коэффициент объемного расширения, который характеризует относительное изменение плотности с температурой ив общем случае определяется выражением:

где u = 1/r - удельный объем жидкости или газа.

Для идеальных газов (или реальных газов под невысоким давлением) с учетом уравнения Клапейрона можно получить такое выражение для b:

Давление р можно представить как сумму гидростатического давления р₀ и избыточного давления p¢: р = р₀ + p¢, при этом выполняется:

(3.6)

Подставляя значение r согласно выражению (3.5) в слагаемое, учитывающее силу тяжести в уравнении (3.1), получим:

С учетом (3.6) последнее уравнение можно записать так: (3.7)

где производная описывается выражениями (3.2); n = m/r₀.

Уравнение (3.7) описывает поле скоростей при свободной конвекции. В развернутом виде в стационарном случае уравнение (3.7) имеет вид:

(3.8)

Три дифференциальных уравнения (3.4) или (3.8) описывают изменение в пространстве четырех скалярных величин: w_x, w_y, w_z и p = p(x,y,x). Поэтому необходимо еще одно уравнение, связывающее эти величины. Этим уравнением является уравнение сплошности или неразрывности, отражающее закон сохранения массы [1]:

(3.9)

Для несжимаемых жидкостей, полагая r = const, из (3.9) получаем:

(3.10)

или, что то же самое,

(3.11)

Отметим, что уравнения движения (3.8), описывающие свободную конвекцию, содержат еще одну переменную скалярную величину: температурное поле , которое описывается уравнением энергии (см. раздел 4). Уравнение энергии, в свою очередь, содержит компоненты скорости w_x, w_y, w_z, поэтому уравнения движения и энергии являются взаимозависимыми, и процессы движения и конвективного теплообмена в общем случае нужно рассматривать совместно. Но пока будем считать, что температурное поле является известным.

Чтобы описать конкретный процесс движения жидкости, нужно задать условия однозначности, включающие в себя геометрические, физические, начальные и граничные условия. Под геометрическими условиями понимаются форма и размеры твердого тела (тел), омываемого жидкостью, в частности, характерный линейный размер тела l. Под физическими условиями понимаются значения теплофизических параметров m, n, r₀, b, а также температурного поля при свободной конвекции. Начальные условия подразумевают задание полей скоростей и давлений в начальный момент времени, но для стационарных задач эти условия не задаются. Граничные условия включают в себя распределения скорости жидкости (или ее производной по нормали к поверхности) на границах рассматриваемого объема:

(3.12)

где x, y, z характеризуют точки на границах изучаемого объема; - вектор скорости на границах объема жидкости. Обычно, задается распределение скорости жидкости на входе в канал или на удалении от поверхности твердого тела. На поверхности твердого тела задаются условия прилипания, которые заключаются в том, что скорость частиц жидкости на поверхности твердого тела равна скорости движения этой поверхности. В случае неподвижной поверхности условие прилипания имеет вид:

(3.13)

т.е. на поверхности твердого тела w_x = w_y = w_z = 0.

Если каким-то способом решить систему уравнений Навье-Стокса (3.4) или (3.8), уравнения сплошности (3.6) с учетом условий однозначности, то получатся следующие зависимости:

где координаты x, y, z являются независимыми переменными; компоненты скорости w_x, w_y, w_z, и давление р – зависимыми переменными.

3.2 Описание уравнений движения жидкости в безразмерном виде

Обычно интерес представляет движение жидкости вдоль поверхности твердого тела. Пусть l – характерный размер тела, которым может быть его длина, ширина, диаметр и т.п. Введем безразмерные декартовые координаты:

Выразим размерные координаты:

(3.14)

Пусть w₀ – характерная скорость жидкости, например, на входе в рассматриваемый объем или на большом удалении от поверхности тела. Введем безразмерные скорости:

Выразим размерные скорости:

(3.15)

В случае свободной конвекции задается характерная температура поверхности t_п и характерная температура жидкости t_ж (например, на удалении от поверхности). Используя характерный температурный напор , введем безразмерную температуру жидкости:

откуда можно выразить размерную избыточную температуру

(3.16)

Декартову ось х для определенности направим в сторону действия силы тяжести, при этом g_x = g; g_y = g_z = 0.

В первом уравнении Навье-Стокса (3.4) для оси x подставим выражения координат и скоростей (3.14) и (3.15):

или

Поделив правую и левую части последнего выражения на , получим:

(3.17)

В уравнении (3.17) имеются безразмерные комплексы:

; (3.18)

.

Комплекс Re называется числом Рейнольдса. Это число характеризует соотношение сил инерции и вязкости в движущейся жидкости. Чем больше скорость жидкости и меньше ее вязкость, тем больше число Re. Число Re является определяющим при вынужденном движении жидкости в закрытых системах (трубах при напорном движении и т.п.).

Комплекс Gaназывается числом Галилея. Этот комплекс играет большую роль при движении жидкости в открытых системах (русла рек, открытые каналы и т.п.) под действием силы тяжести. В закрытых системах сила тяжести полностью компенсируется силой гидростатического давления, и комплекс Ga не влияет на движение жидкости.

Комплекс Eu называется числом Эйлера, он характеризует соотношение статического давления к динамическому. Комплекс Eu является определяемым, и т.к. он находится под знаком производной, то его обычно записывают в виде

,

где Dр = р – р₀; р₀ – начальное давление жидкости, например, давление на входе в рассматриваемый канал, сечение и т.п. В качестве Dр может выступать потеря давления на некотором участке канала.

С учетом обозначений (3.18), уравнение (3.17) запишем так:

(3.19а)

Если привести второе и третье уравнения (3.4) к безразмерному виду, то они примут следующие выражения:

(3.19б)

(3.19в)

Аналогичным способом приведем к безразмерному виду уравнения (3.8), описывающие поле скоростей при свободной конвекции, при этом используем выражения (3.14), (3.15) и (3.16) для координат, скорости и температуры. Первое уравнение (3.8) в безразмерном виде примет вид:

(3.20)

где - безразмерная температура; Gr – безразмерный критерий, который носит название числа Грассгофа, и определяется выражением:

.

Поскольку из выражения (3.5) следует, что

где Dr - уменьшение плотности жидкости при увеличении температуры на , то число Грассгофа можно записать еще таким образом:

где Ar – число Архимеда, определяемое обычно выражением:

где под r₀ и r обычно понимают плотности двух сосуществующих фаз (например, плотности жидкости и пара в процессах кипения данной жидкости).

Критерий Грассгофа Gr (или его разновидность число Архимеда Ar) определяет подъемную силу, которая возникает при свободной конвекции. Данный критерий является определяющим в процессах свободной конвекции.

Остальные уравнения (3.8) (второе и третье) после приведения к безразмерному виду, очевидно, примут такой же вид, как выражения (3.19б) и (3.19в).

Уравнение неразрывности (3.10) после приведения к безразмерному виду будет выглядеть следующим образом:

или

(3.21)

при этом новых безразмерных комплексов здесь не появляется.

Граничное условие (3.12) в безразмерном виде записывается так:

(3.22)

где - безразмерная скорость на границах объема жидкости; X, Y, Z – безразмерные координаты точек на границах. В частности, на поверхности твердого тела выполняется условие прилипания:

3.3 Уравнения подобия для процессов движения жидкости

Из решения системы уравнений (3.19) и (3.21), описывающих движение жидкости при вынужденной конвекции в открытых системах (в руслах каналов, рек), можно получить следующие уравнения подобия:

(3.23)

В данном случае определяющими числами подобия являются X, Y, Z и число Галилея Ga, а определяемыми числами подобия – W_x, W_y, W_z и число Рейнольдса Re. Определение числа Эйлера Eu (безразмерного давления) в данных задачах не представляет интереса, поскольку в направлении движения жидкости градиент давления обычно равен нулю, а в остальных направлениях определяется изменением гидростатического давления.

При вынужденном напорном движении жидкости в закрытых системах уравнения подобия, получаемые при решении системы уравнений (3.19) и (3.21), принимают вид:

(3.24)

В данном случае число Галилея Ga не играет роли и выпадает из уравнений подобия, поскольку сила тяжести полностью компенсируется гидростатическим давлением. Определяющими числами подобия являются X, Y, Z и число Рейнольдса Re, а определяемыми – W_x, W_y, W_z и число Эйлера Eu.

При больших Рейнольдса (Re®¥) в процессах вынужденного напорного движения жидкости наступает автомодельность относительно данного критерия. В этом случае уравнения подобия (3.24) принимают вид:

(3.25)

При свободной гравитационной конвекции жидкости, как следует из уравнений (3.20) и (3.21), уравнения подобия принимают вид:

(3.26)

В данном случае определяющими числами подобия являются X, Y, Z и число Грассгофа Gr, а определяемыми – W_x, W_y, W_z и число Рейнольдса Re. Определение числа Эйлера Eu в данных задачах не представляет интереса, поскольку градиент давления практически определяется изменением гидростатического давления.

Наконец, при наличии одновременно вынужденного (напорного) и свободного движения, как следует из уравнений (3.19б), (3.20) и (3.21), уравнения подобия выглядят следующим образом:

(3.27)

В данном случае определяющими числами подобия являются X, Y, Z, число Рейнольдса Re и число Грассгофа Gr, а определяемыми – W_x, W_y, W_z и число Эйлера Eu.

Если кроме одного характерного линейного размера l имеются другие характерные размеры омываемых твердых тел l₁, l₂ и т.д., то в уравнения подобия вводятся безразмерные симплексы (простые числа подобия): L₁ = l₁/l, L₂ = l₂/l, и т.д. Тогда, например, последнее уравнение подобия в (3.27) будет иметь следующий вид:

Если рассматривается характерная точка в жидкости с координатами X_x, Y_x, Z_x, то уравнения подобия (3.27), примут вид:

(3.28)

Если свободная конвекция отсутствует, то уравнения подобия (3.28) для характерной точки в жидкости принимают вид:

(3.28)

Если выполняется автомодельность относительно критерия Re, то уравнения (3.28) вырождаются в постоянные значения:

Если имеет место только свободная конвекция, то уравнения подобия (3.28) для характерной точки в жидкости принимают следующий вид:

(3.29)

Определение числа Eu при свободной конвекции обычно не представляет интереса.

3.4. Моделирование процессов движения жидкости

При моделировании изучение процесса в образце заменяется исследованием этого же процесса на модели. Если процесс в модели будет подобен процессу в образце, то результаты исследования на модели могут быть применены к образцу. Моделирование, по существу, включает в себя две самостоятельные задачи. Во-первых, в модели необходимо осуществить процесс, подобный процессу, происходящему в образце, и во-вторых, выполнить на модели все требуемые измерения и наблюдения.

Для того, чтобы процессы движения жидкости в образце и модели были подобными, необходимо осуществить три условия подобия.

Во-первых, нужно, чтобы процессы в модели и образце были качественно одинаковыми, т.е. имеющими одинаковую физическую природу, и описывались одинаковыми дифференциальными уравнениями.

Во-вторых, необходимо, чтобы условия однозначности подобных процессов (в образце и модели) были одинаковы во всем, кроме числовых значений постоянных величин, содержащихся в этих условиях. Условия однозначности для стационарных процессов состоят:

1) из геометрических условий, характеризующих форму и размеры тела, в котором протекает процесс;

2) из физических условий, характеризующих физические свойства рассматриваемой среды;

3) из граничных условий, характеризующих особенности протекания процесса на границах жидкости.

Таким образом, необходимо осуществить геометрическое подобие образца и модели. Все размеры образца и модели, существенные для процесса движения жидкости, должны быть связаны между собой соотношением l = с_l×l¢, где l и l¢ - характерные линейные размеры образца и модели. Т.е. модель должна быть построена как точная копия образца, уменьшенная в с_l раз. Конечно, копироваться должна не внешняя форма образца, а внутренняя конфигурация каналов, по которым движутся газы или жидкости.

Обычно, геометрическое подобие осуществить нетрудно. Следует только иметь в виду, что изменение геометрических размеров не должно привести к качественному изменению процесса в модели. Например, при течении газа в трубе за характерный размер l может быть принят диаметр трубы d. Если средняя длина свободного пробега молекул будет примерно больше 0,001d, то условия прилипания (3.13), характерные для сплошных сред, перестают выполняться, и будет происходить как бы проскальзывание газа вблизи поверхности твердого тела.

Необходимо также осуществить подобие физических условий для образца и модели. Если физические параметры (m, n, r, b) постоянны, то это особых трудностей не составляет. Однородные физические параметры в образце и модели должны быть связаны соответствующим масштабом преобразования:

j = c_j×j¢,

где j и j¢ - физический параметр в образце и модели; c_j - константа подобия для данного физического параметра. При этом, если физические свойства жидкости в модели и образце одни и те же, c_j = 1.

При наличии теплообмена в жидкости, ее температура по объему изменяется, и в общем случае изменяются физические параметры, которые в большей или меньшей степени являются функцией температуры. В этом случае точное подобие физических условий обеспечить гораздо сложнее, а иногда и невозможно. Тогда осуществляют приближенное моделирование.

При свободном движении жидкости теплообмен обычно всегда присутствует, и для подобия физических условий необходимо, чтобы было равенство безразмерных температур в объеме жидкости в модели и в образце при одинаковых безразмерных координатах

X ¢ = X, Y¢ = Y, Z¢ = Z:

(3.29)

При моделировании необходимо также осуществить подобие процессов на границах исследуемой жидкости в модели и в образце. При этом, например, должно выполняться равенство безразмерных скоростей на границах изучаемого объема жидкости:

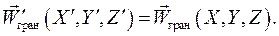(3.30)

При вынужденной конвекции чаще всего выполнение условия (3.30) ограничивается требованием подобия условий входа жидкости в образец и модель (чтобы обеспечить подобное распределение скоростей на входе). Подобия условий входа жидкости можно достичь путем устройства входного участка модели геометрически подобным входному участку образца.

При свободной и вынужденной конвекции выражение (3.30) обеспечивается автоматически на поверхностях тел, ограничивающих объем жидкости, если в модели и в образце жидкость можно считать сплошной средой:

В третьих, для подобия процессов в образце и модели необходимо чтобы определяющие одноименные критерии подобия в образце и модели имели одинаковые значения. Тогда и определяемые безразмерные переменные в образце и модели также будут иметь одинаковые значения.

Допустим, изучается вынужденное напорное движение жидкости. Уравнения подобия в этом случае описываются выражениями (3.24). Определяющим критерием подобия (кроме переменных координат X, Y, Z) является число Рейнольдса Re. Для подобия процессов в модели и в образце требуется выполнение равенства: Re¢ = Re, или:

(3.31)

где - характерные скорости жидкости в модели и образце; n¢, n - коэффициенты кинематической вязкости жидкости в модели и в образце.

Если в модели и образце протекает одна и та же жидкость (n¢ = n, с_n = 1), то из (3.31) следует, что должно выполняться соотношение

Например, если модель в 10 раз меньше образца (c_l = 10), то скорость жидкости в модели должна быть в 10 раз больше, чем в образце.

Из (3.31) можно найти константу подобия по скорости:

(3.32)

где , - константы подобия по вязкости и линейному размеру.

Из равенства Re¢ = Re и из уравнений подобия (3.24) следует, что для сходственных точек модели и образца

X ¢ = X, Y¢ = Y, Z¢ = Z

будут одинаковы безразмерные скорости и числа Эйлера:

или, в развернутом виде:

где x¢, y¢, z¢ - декартовы координаты в модели; x, y, z - декартовы координаты в образце; - компоненты скорости жидкости в модели; - компоненты скорости жидкости в образце; Dp¢, Dp - изменение давления в модели и в образце; r¢, r - плотность жидкости в модели и в образце.

Последние выражения можно представить таким образом:

(3.33)

где - константа подобия для плотности.

После измерения величин , Dp¢ на модели, используя выражения (3.33) можно определить величины , Dp в образце.

Если процессы движения жидкости в образце и в модели автомодельны относительно числа Re, то при вынужденном движении не обязательно выдерживать равенство этого критерия для образца и модели.

В случае свободной конвекции для подобия процессов в модели и образце нужно обеспечить равенство чисел Грассгофа: Gr¢ = Gr, или в развернутом виде

, (3.34)

где - характерные температурные напоры в модели и образце; b¢, b - температурные коэффициенты объемного расширения в модели и образце. Если в модели и образце используется одна и та же жидкость (b¢ = b, n¢ = n), тогда, как следует из (3.34), должно выполняться соотношение:

.

Если с_l = 2, то температурный напор в модели должен быть в 8 раз больше температурного напора в образце .

При выполнении условия (3.34) для сходственных точек образца и модели будут выполняться условия

(3.35)

В случае вынужденной конвекции при безнапорном движении жидкости для подобия процессов в модели и образце нужно обеспечить равенство чисел Галилея: Ga¢ = Ga, или в развернутом виде

, (3.36)

где g¢, g - проекции ускорения свободного движения на направление движения жидкости в образце и модели. Чтобы обеспечить условие (3.35), можно изменять угол наклона g канала, где движется жидкость, по отношению к вертикали. При этом величина g¢ изменяется согласно выражению g¢ = g₀×cos g, где g₀ = 9,81 м/с².

При выполнении условия (3.36) для сходственных точек образца и модели будут выполняться условия (3.35).

Вопросы для самоконтроля:

1) Какие виды движения жидкости вы знаете?

2) Напишите уравнение Навье-Стокса для вынужденного движения жидкости и объясните его физический смысл.

3) Напишите выражение для полной производной скорости по времени. Чем она отличается от частной производной?

4) Напишите уравнение неразрывности (сплошности). Какой физический закон оно отражает?

5) Чем обусловлено возникновение свободной конвекции жидкости в гравитационном поле Земли?

6) Напишите выражение для определения температурного коэффициента объемного расширения жидкости.

7) Напишите уравнение Навье-Стокса, описывающее поле скорости при свободной конвекции.

8) Напишите выражения для безразмерных чисел подобия Re, Eu и объясните их физический смысл.

9) Напишите выражения для безразмерных чисел подобия Ga, Gr, Ar и объясните их физический смысл.

10) Какие критерии подобия являются определяющими и определяемыми при вынужденном напорном движении жидкости?

11) Какие критерии подобия являются определяющими и определяемыми при свободной конвекции жидкости?

12) Сформулируйте условия прилипания и поясните, для каких сред они выполняются.

13) В каких процессах движения жидкости число Галилея Ga является определяющим?

14) При каком условии наступает автомодельность вынужденного напорного движения жидкости относительно числа Re?

15) Напишите уравнения подобия при вынужденном безнапорном движении жидкости.

16) Сформулируйте условия моделирования процессов движения жидкости.

17) Что понимается под граничными условиями в процессах движения жидкости?

Выводы по главе

В данном разделе приведены уравнения, описывающие движения реальной жидкости при вынужденной и свободной конвекции, включающие в себя уравнения Навье-Стокса и уравнение неразрывности (сплошности). Сформулированы условия однозначности для описания процессов движения жидкости, включающие геометрические, физические и граничные условия. Получены уравнения движения жидкости в безразмерном виде. Установлены определяющие и определяемые критерии подобия при вынужденном напорном и безнапорном движении, и при свободной конвекции. Установлены уравнения подобия для процессов движения жидкости в общем и частных случаях. Рассмотрены условия моделирования процессов движения жидкости при вынужденной и свободной конвекции.

Список литературы по теме

1. Исаченко В.П. Теплопередача: Учебник для вузов / В.П. Исаченко, В.А. Осипова, А.С. Сукомел. – 4-е изд., перераб. и доп. – М.: Энергоиздат, 1981. – 416 с.

2. Кутателадзе С.С. Моделирование теплоэнергетического оборудования / С. С. Кутателадзе, В. А. Пермяков, Д. Н. Ляховский. – М.: Энергия 1966.

3. Мигай В.К. Моделирование теплообменного энергетического оборудования / В.К. Мигай. – Л.: Энергоатомиздат. Ленингр. Отд-ние, 1987. – 264 с.: ил.

4. Тепло- и массообмен. Теплотехнический эксперимент: Справочник / Е.В. Аметистов, В.А. Григорьев, Б.Т. Емцев и др.; под общей редакцией В.А. Григорьева и В.М. Зорина. – М.: Энергоиздат, 1991. – 512 с., ил.