Тема 3. Теоремы сложения и умножения вероятностей
Теоретические сведения
Объединение событий
Вероятность объединения двух несовместных событий ( 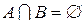 ):
): 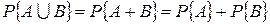 .
.
В общем случае 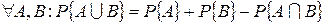 .
.
Вероятность объединения нескольких несовместных событий:
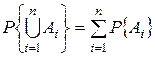 .
.
В общем случае
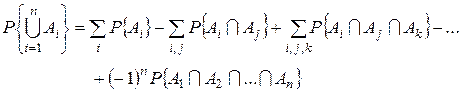 .
.
Если события 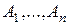 образуют полную группу, то
образуют полную группу, то 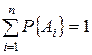 . Сумма вероятностей противоположных событий
. Сумма вероятностей противоположных событий 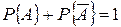 .
.
Пересечение событий
Вероятность события А при условии, что осуществилось событие В, называется условной вероятностью и обозначается 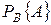 . События А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Для независимых событий
. События А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Для независимых событий 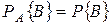 и
и 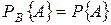 . Вероятность пересечения двух событий
. Вероятность пересечения двух событий 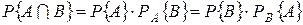 . Для независимых событий:
. Для независимых событий: 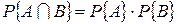 . Вероятность пересечения нескольких событий:
. Вероятность пересечения нескольких событий: 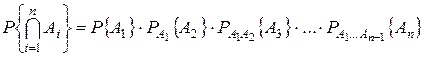 . Для независимых событий:
. Для независимых событий: 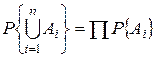 .
.
Упражнения
1) В урне 10 белых и 8 черных шаров. Из урны в случайном порядке, один за другим, вынимают все находящиеся в ней шары. Найти вероятность того, что вторым по порядку будет вынут белый шар.
2) В урне 8 белых, 10 черных и 6 красных шаров. Три из них вынимаются наугад. Найти вероятность того, что по крайней мере два их них будут одноцветными.
3) Ведется стрельба по самолету. Чтобы поразить самолет, достаточно поразить два двигателя вместе или кабину пилота. Вероятность поражения первого двигателя равна 0.7, второго – 0.8, кабины пилота – 0.6. Агрегаты самолета поражаются независимо друг от друга. Найти вероятность того, что самолет будет выведен из строя.
4) В партии, состоящей из 50 деталей, имеется 10 дефектных. Из партии выбирается для контроля 5 изделий. Если среди контрольных окажется 3 дефектных, бракуется вся партия. Найти вероятность того, что партия будет забракована.
5) Прибор состоит из п блоков. Выход из строя каждого блока означает выход из строя прибора в целом. Блоки выходят из строя независимо друг от друга. Вероятность безотказной работы (надежность) каждого блока равна р. Найти надежность Р прибора в целом.
6) Для повышения надежности прибора он дублируется другим точно таким же прибором. Надежность каждого прибора равна р. При выходе из строя первого прибора происходит мгновенное переключение на второй. Надежность переключающего устройства равна 1. Определить надежность этой системы.
7) В условиях предыдущей задачи надежность переключающего устройства равна р1.
8) Для повышения надежности прибора он дублируется (п-1) другими такими же приборами. Надежность каждого прибора равна р. Найти надежность системы. Сколько надо взять приборов чтобы повысить надежность до заданной Р1?
9) Водопроводчик Вася поздно вечером возвращается домой. У него в руках связка из пяти ключей, причем только один подходит к дверям квартиры. По причинам, о которых можно только догадываться, Вася пробует ключи наугад так, что при каждой попытке любой ключ, включая нужный, выбирается с одинаковой вероятностью. За этим захватывающим зрелищем через замочную скважину дверей соседней квартиры внимательно следят Иван Кузьмич и Пелагея Марковна. Иван Кузьмич готов биться об заклад, что Васька и с третей попытки в дом не попадет. Сердобольная же Пелагея Марковна утверждает, что, по крайней мере, на третий раз дверь поддастся. У кого больше шансов победить в споре?
10) Ослик Иа-Иа к словам песенки "и-а" пытается наугад подобрать мелодию. Какова вероятность того, что ему это удастся хотя бы на 40-ой раз? (Указание: а) ослиному крику соответствует сочетание нот ля-до; б) ослик пользуется основной октавой и уже проверенные парные сочетания не запоминает, но безошибочно отреагирует на подходящую.)
11) Симпатичная студентка Люся Копейкина к зачету успела выучить только 10 вопросов из 20, но надеется, что в случае неудачи уговорит профессора Аркадия Аристарховича задать ей второй вопрос. По многолетним наблюдениям профессора можно разжалобить в двух случаях из трех, и это соотношение не меняется с годами. Каковы Люсины шансы сдать зачет?
12) Симпатичная студентка Люся Копейкина знает к зачету только 15 вопросов из 30. Она считает, что если пойдет отвечать вторая, то ее шансы вытянуть счастливый билет увеличатся. Права ли она? Докажите.
13) Студент филфака Петя Чернышев ставит три ящика пива против двух, что, выучив 12 билетов из 30, он сдаст зачет по крайней мере со второго раза. Стоит ли его приятелю заключать пари? (Указание: найти отношение вероятностей благоприятного и неблагоприятного для Пети событий.)
