Решение систем уравнений

Решение систем уравнений матричным методом.

Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х1, х2, …, хn:

Система линейных уравнений может быть записана в матричном виде: Ах = b, где:

Если det A ≠ 0 то система или эквивалентное ей матричное уравнение имеет единственное решение.

Решение систем уравнений с помощью функции Lsolve

Системы линейных уравнений удобно решать с помощью функции lsolve. Функция lsolve(А, b) - возвращает вектор решения x такой, что Ах = b.

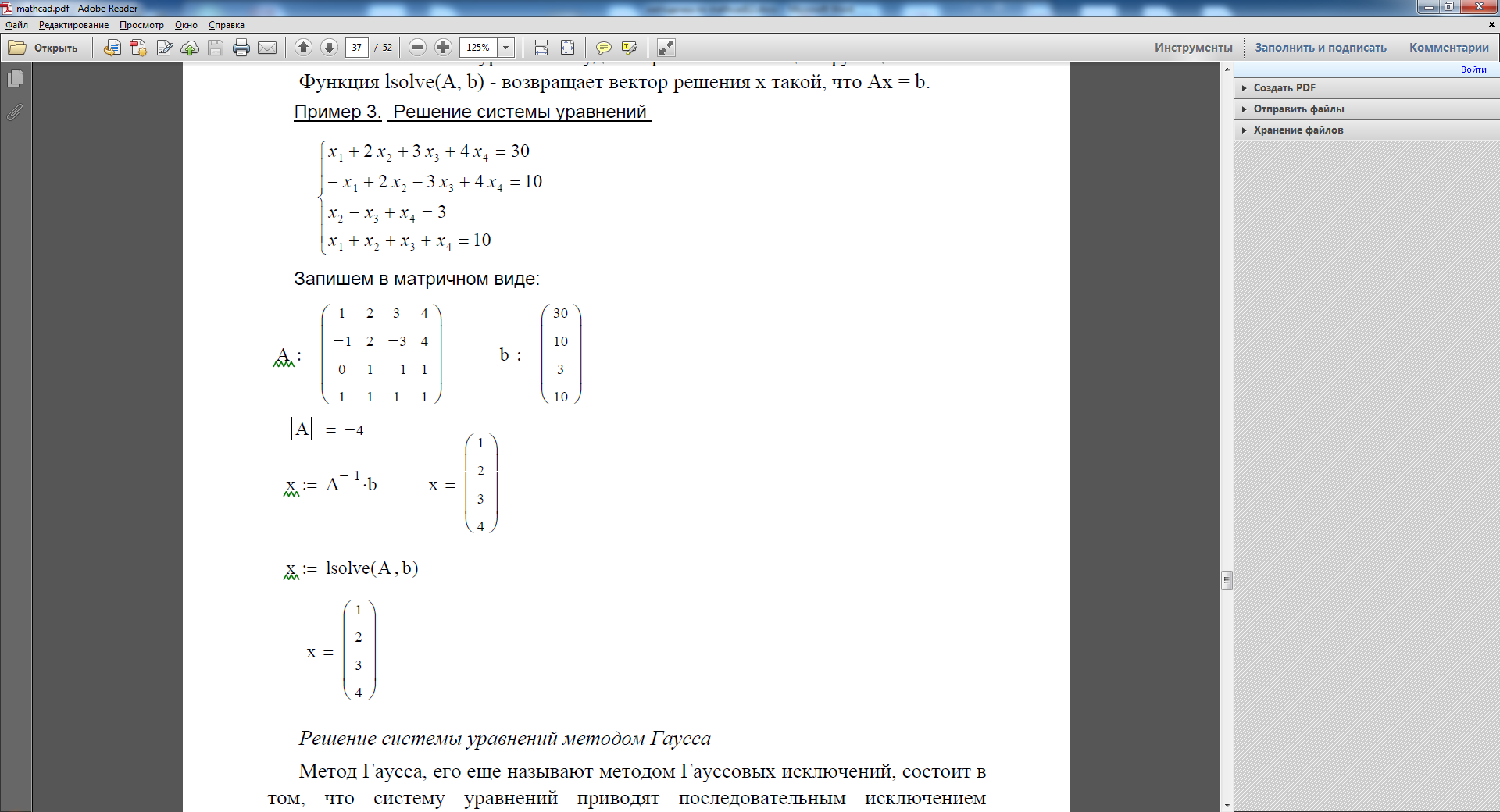
Решение системы уравнений методом Гаусса

Метод Гаусса, его еще называют методом Гауссовых исключений, состоит в том, что систему уравнений приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей.

В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями над строками приводят расширенную матрицу системы к ступенчатому виду, а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица. Последний, (n + 1) столбец этой матрицы содержит решение системы.

В MathCAD прямой и обратный ходы метода Гаусса выполняет функция rref(A).

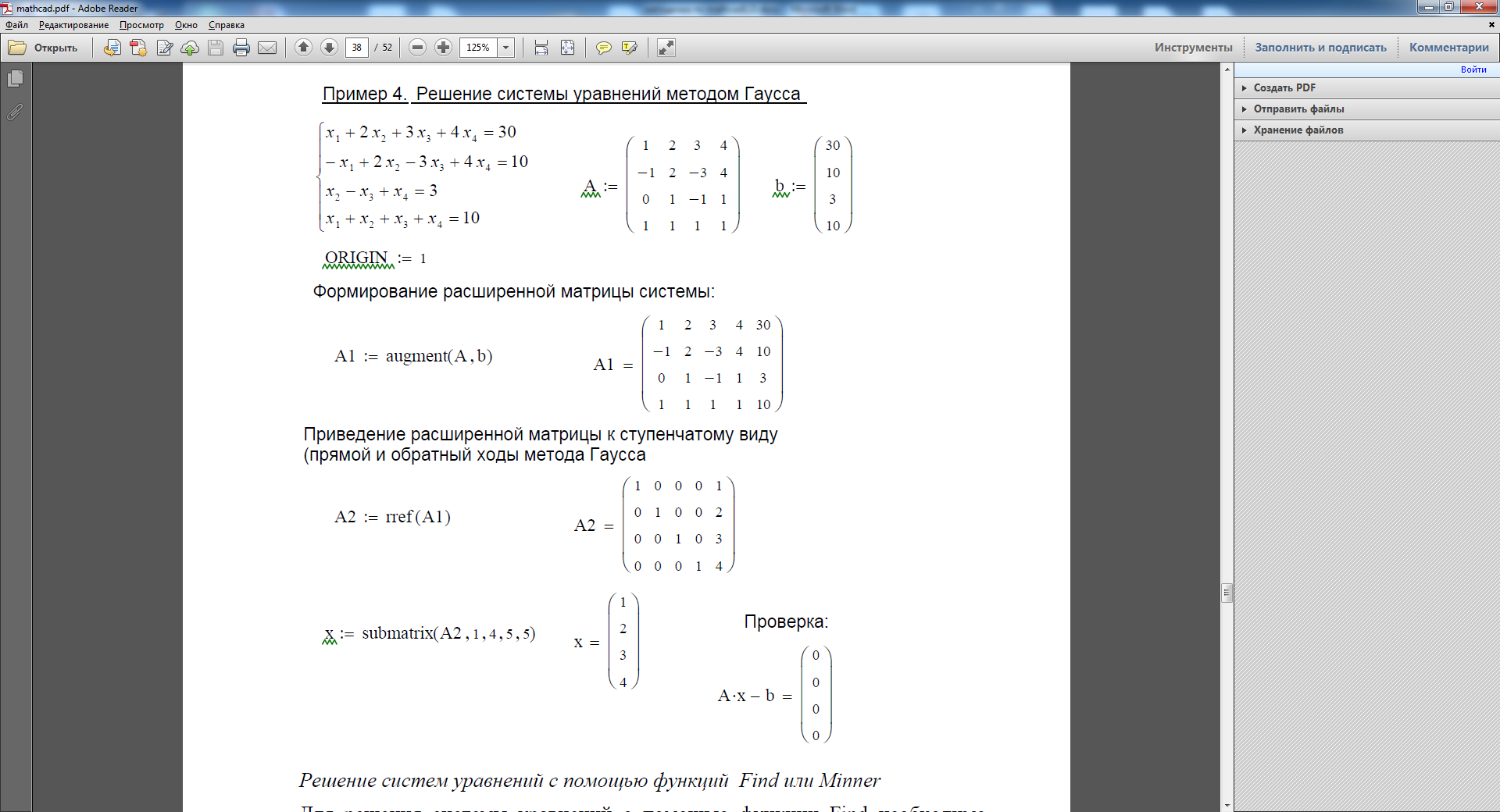
Решение систем уравнений с помощью функций Find или Minner

Для решения системы уравнений с помощью функции Find необходимо выполнить следующее:

1. Задать начальное приближение для всех неизвестных, входящих в систему уравнений. MathCAD решает систему с помощью итерационных методов;

2. Напечатать ключевое слово Given. Оно указывает MathCAD, что далее следует система уравнений;

3. Введите уравнения и неравенства в любом порядке. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов <, >, ≥ и ≤;

4. Введите любое выражение, которое включает функцию Find, например: х:= Find(х, у). Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое - либо выражение, содержащее функцию Find, называют блоком решения уравнений.

Функция Minner очень похожа на функцию Find (использует тот же алгоритм). Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minner возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке.

Правила использования функции Minner такие же, как и функции Find. Функция Minerr(x1, x2, . . .) -возвращает приближенное решение системы уравнений. Число аргументов должно быть равно числу неизвестных.

Символьное решение уравнений

Имеются некоторые задачи, для которых возможности MathCAD позволяют находить решения в символьном (аналитическом) виде. Решение уравнений в символьном виде позволяет найти точные или приближенные корни уравнения:

• если решаемое уравнение имеет параметр, то решение в символьном виде может выразить искомый корень непосредственно через параметр. Поэтому вместо того чтобы решать уравнение для каждого нового значения параметра, можно просто заменять его значение в найденном символьном решении;

• если нужно найти все комплексные корни полинома со степенью меньше или равной 4, символьное решение даст их точные значения в одном векторе или в аналитическом или цифровом виде.

Команда Символы→ Переменные→ Вычислитьпозволяет решить уравнение относительно некоторой переменной и выразить его корни через остальные параметры уравнения.

Чтобы решить уравнение символьно, необходимо:

1. Напечатать выражение (для ввода знака равенства используйте комбинацию клавиш Ctrl + =);

2. Выделить переменную, относительно которой нужно решить уравнение, щелкнув на ней мышью;

3. Выбрать пункт меню Символы → Переменные → Вычислить.

Нет необходимости приравнивать выражение нулю. Если MathCAD не находит знака равенства, он предполагает, что требуется приравнять выражение нулю.

Чтобы решить систему уравнений в символьном виде, необходимо выполнить следующее:

1. Напечатать ключевое слово Given;

2. Напечатать уравнения в любом порядке ниже слова Given. Удостоверьтесь, что для ввода знака = используется Ctrl + =;

3. Напечатать функцию Find, соответствующую системе уравнений;

4. Нажать Ctrl + .(клавиша CTRL, сопровождаемая точкой). MathCAD отобразит символьный знак равенства →;

5. Щелкнуть мышью на функции Find.

4.5 Задания к лабораторной работе 3

Задание № 1

Построить график функции f(x) и приблизительно определить один из корней уравнения. Решить уравнение f(x) = 0 с помощью встроенной функции MathCAD root.

вариант	f(x)	вариант	f(x)
1, 31	4sin x + x2 - 2=0	16, 46	(x - 1)2 - 0.5exp( - x) – 2=0
2, 32	3X-4.5x-5.6=0	17, 47	2/x+x2 + ex – 8=0
3, 33	3 sin x +0.35x-8x=0	18, 15	tgx + x + 2=0
4, 34	0.25x2+x-1.25002=0	19, 49	ctgx – 2x + 2=0
5, 35	0.1x2-xlnx=0	20, 50	-x2 + cos (x+1) + 3=0
6, 36	3x - 4lnx-5=0	21, 51	2ln(2–x)–x + ex – 10=0
7, 37	ex - e –x -2=0	22, 52	1/x + ln(2x + 4) – 3=0
8, 38	ex + lnx – 10x=0	23, 53	x× cos x + 1.5=0
9, 39	sin x2+cos x2-10x=0	24, 54	2x5 – lnx – 7x2=0
10, 40	x2-ln(1+x)-3=0	25, 55	x×sinx x + 1.5=0
11, 41	2xsin x – cosx=0	26, 56	x2x – 4x2 + 1.5=0
12, 42	lnx – x + 1.8=0	27, 57	2.5x – 8.6x – 3.5=0
13, 43	0.6 ×3x – 2.3x – 3=0	28, 58	ln(x + 2) + 2x2 - 9x + 2=0
14, 44	2x – 4x=0	29, 59	xln(2.5x) – 1.5x + 1.5=0
15, 45	3x – ex + 4=0	30, 60	xtgx – 1/3=0

Задание № 2

Для полинома g(x) выполнить следующие действия:

1. с помощью команды Символы→ Коэффициенты полиномасоздать вектор V, содержащий коэффициенты полинома;

2. решить уравнение g(x) = 0 с помощью функции polyroots;

3. решить уравнение символьно, используя команду Символы→Переменные→ Вычислить.

вариант		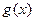вариант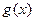
1, 31		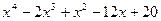16, 46	x5 – 2.2x3 + 0.5x2 – 7x – 3.4
2, 32		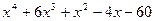17, 47	x5-3.2x3+2.5x2-7x-2.4
3, 33		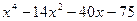18, 15	x5-5.2x3+2.5x2-7x-2.4
4, 34		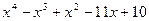19, 49	x5-4.2x3+3.5x2-7x-7.4
5, 35		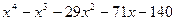20, 50	x5-2.2x3+7.5x2-7x-3.9
6, 36		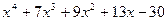21, 51	x5-2.9x3+6.5x2-7x-5.4
7, 37		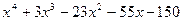22, 52	x5-3.2x3+9.5x2-7x-7.5
8, 38		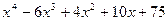23, 53	x5-3.5x3+2.5x2-7x+6.4
9, 39		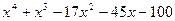24, 54	x5-9.2x3+5.5x2-7x+1.4
10, 40		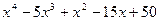25, 55	x5-8.2x3+4.5x2-7x+6.5
11, 41		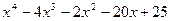26, 56	x5-3.2x3+2.5x2-7x+1.5
12, 42		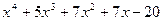27, 57	x5-7.2x3+9.5x2-7x+2.5
13, 43		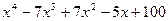28, 58	x5-5.2x3+5.5x2-7x+3.5
14, 44		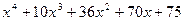29, 59	x5-1.2x3+8.5x2-7x+4.5
15, 45		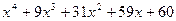30, 60	x5-3.2x3+1.5x2-7x+9.5

Задание № 3

Решить систему линейных уравнений:

1. матричным способом и используя функцию lsolve;

2. методом Гаусса;

3. используя функцию Find.

Вариант	Система линейных уравнений	Вариант	Система линейных уравнений
1,31		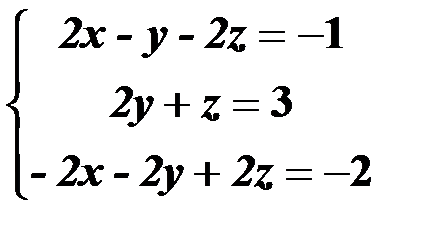16,46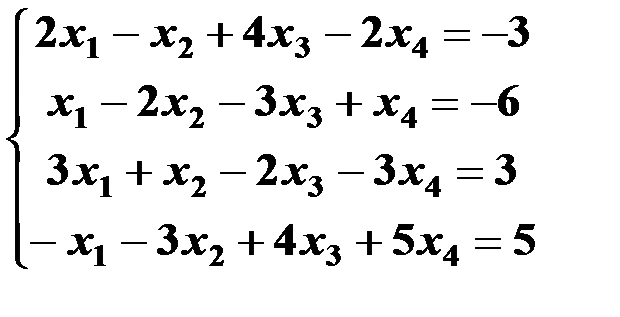
2,32		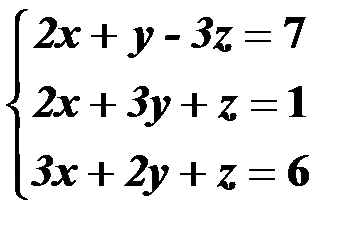17,47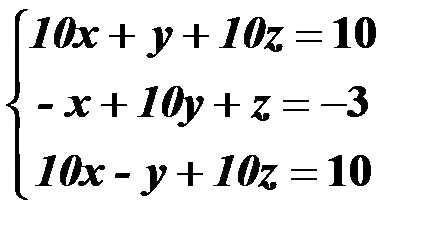
3,33		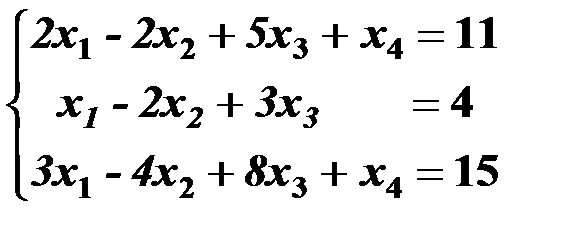18,48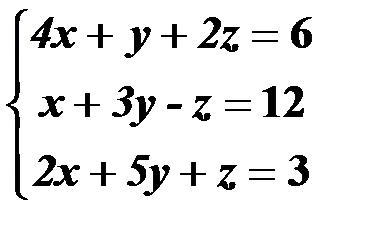
4,34		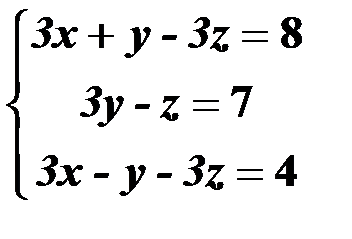19,49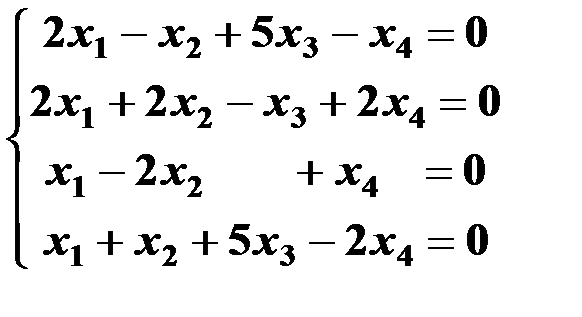
5,35		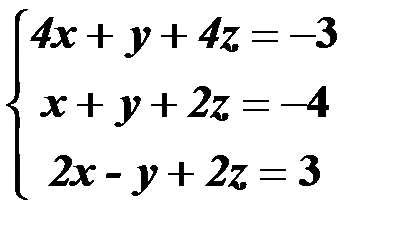20,50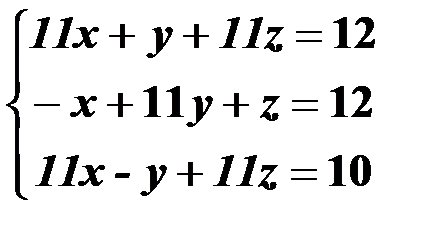
6,36		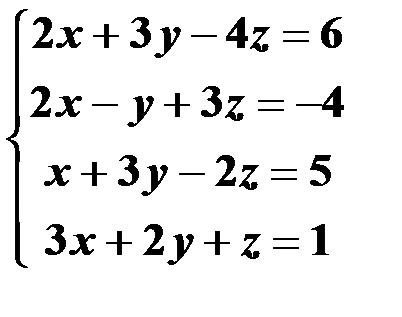21,51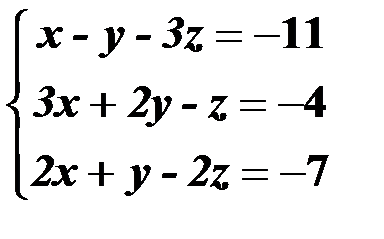
7,37		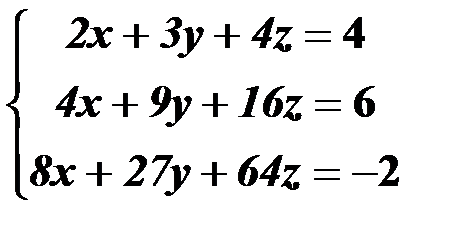22,52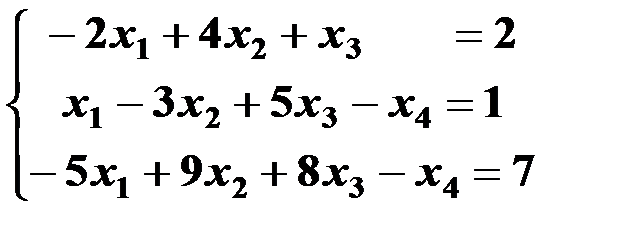
8,38		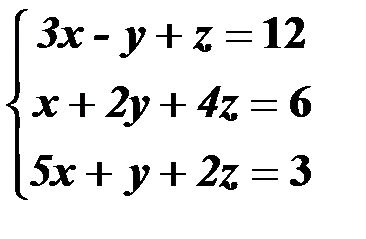23,53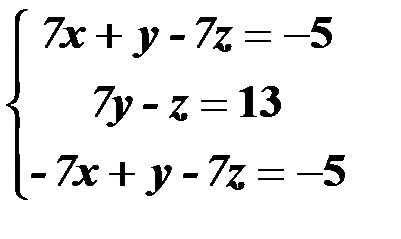
9,39		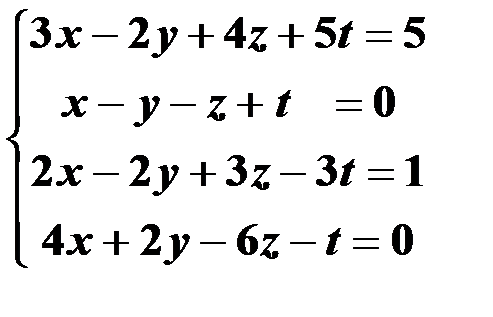24,54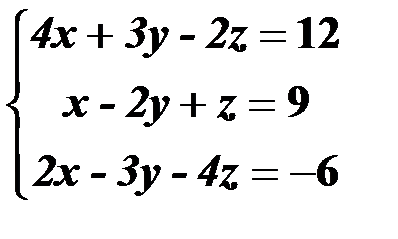
10,40		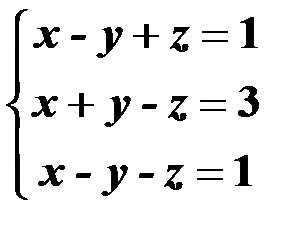25,55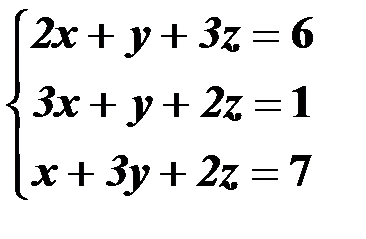
11,41		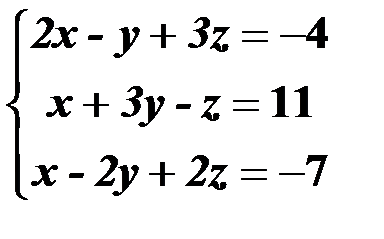26,56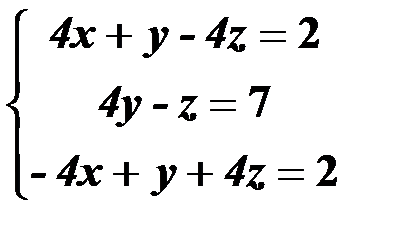
12,42		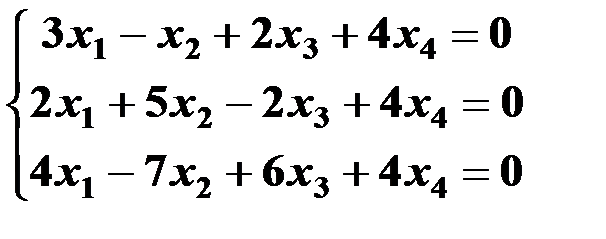27,57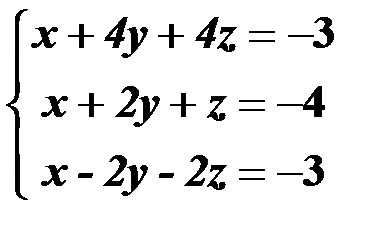
13,43		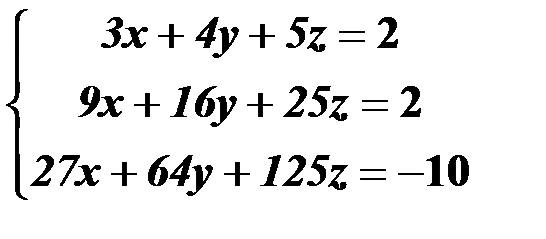28,58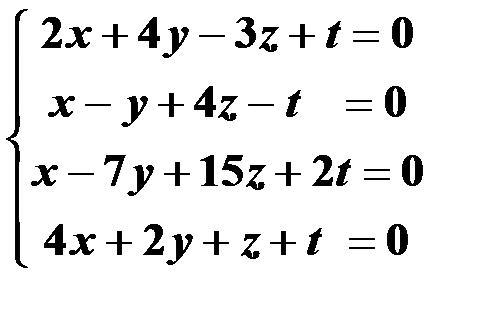
14,44		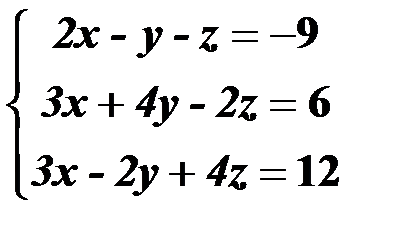29,59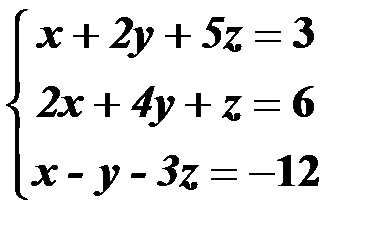
15,45		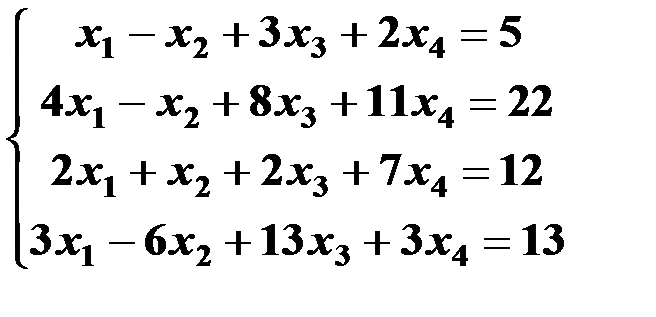30,60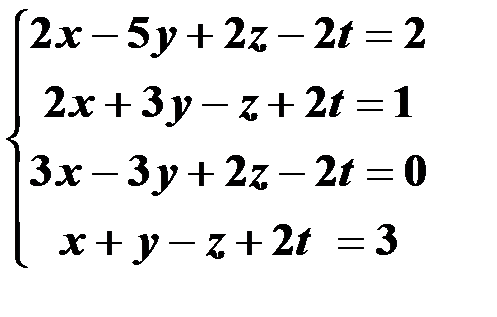

Задание № 4.

Для полинома g(x) выполнить следующие действия:

1) разложить на множители, используя операцию Символы → Фактор;

2) подставьте выражение x = y + z в g(x), используя операцию Символы → Переменные → Замена (предварительно скопировав подставляемое выражение в буфер обмена, выделив его и нажав комбинацию клавиш Ctrl + C);

3) используя операцию Символы → Расширить, разложите по степеням выражение, полученное в 2);

4) используя операцию Символы → Подобные, сверните выражение, полученное в 3), по переменной z.

Задание № 5.

1) Найти первообразную аналитически заданной функции f(x), используя операцию Символы ⇒ Переменные ⇒ Интеграция.

2) Определить символьное значение первой и второй производных f(x), используя команду Символы ⇒ Переменные ⇒ Дифференциалы.

Контрольные вопросы

1. Какие символьные преобразования можно выполнять в MathCAD?

2. Как можно решить нелинейное уравнение в MathCAD?

3. Как найти начальное приближение корня уравнения?

4. Для чего используются функции root? polyroots?

5. Как можно решить систему линейных уравнений?

6. Как построить график?

7. Как построить несколько графиков в одной системе координат?

8. Как построить декартовый график?

9. Как отформатировать построенный график?

10. Как построить график кривой, заданной параметрически?

11. Как построить график в полярной системе координат?

12. Как построить график поверхности?