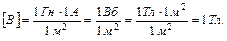Динамика поступательного движения
· Согласно второму закону Ньютона:
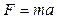 , или
, или 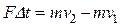 ,
,
где m - масса тела; а – ускорение, приобретенное им под действием силы F; v1 и v2 – начальная и конечная скорости.
· Закон сохранения импульса (количество движения):
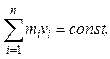
или для двух тел (i=2)
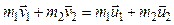 ,
,
где 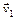 и
и 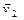 – векторы скоростей тел до взаимодействия;
– векторы скоростей тел до взаимодействия; 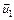 и
и 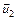 – векторы скоростей тех же тел после взаимодействия.
– векторы скоростей тех же тел после взаимодействия.
· Силы, рассматриваемые в механике:
а) сила тяжести: 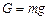 ;
;
б) сила трения скольжения: 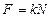 ,
,
где k – коэффициент трения скольжения; N - сила нормального давления.
в) сила упругости: 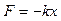 ,
,
где k – коэффициент упругости (жесткость пружины), х – абсолютная деформация;
г) сила гравитационного взаимодействия: 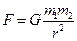 ,
,
где G – гравитационная постоянная; m1 и m2 - массы тел; r – расстояние между телами.
· Работа постоянной силы F на пути S:
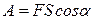 ,
,
где a – угол между направлением силы и пути.
· Мощность постоянной силы:
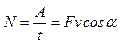 ,
,
где v – скорость движения.
· Кинетическая энергия тела массой m, движущегося поступательно со скоростью 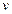 ,
,
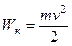 .
.
· Потенциальная энергия упруго деформируемого тела:
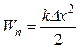 ,
,
где Dх – величина деформации; k – коэффициент упругости.
· Потенциальная энергия тяготения двух шарообразных тел (или материальных точек) с массами m1 и m2:
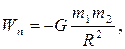
где R – расстояние между телами; G – гравитационная постоянная.
· Потенциальная энергия тела массой m, приподнятого на небольшую высоту h над землей:
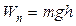 .
.
Динамика вращательного движения
· Момент силы F относительно некоторой оси вращения:
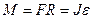 ,
,
где R – расстояние между линией действия силы и осью вращения; J – момент инерции; e – угловое ускорение.
· Моменты инерции некоторых тел массой m относительно оси, проходящей через центр масс:
а) диска (цилиндра): 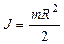 ,
,
где R - радиус диска (цилиндра);
б) материальной точки: 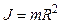 ;
;
в) тонкого стержня длиной l: 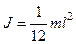 ;
;
г) шара с радиусом R: 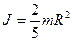 .
.
· Закон сохранения момента импульса:
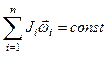 или для двух тел (i=2),
или для двух тел (i=2),
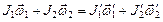 ,
,
где 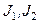 и
и 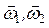 – моменты инерции тел и угловые скорости в начальный момент времени;
– моменты инерции тел и угловые скорости в начальный момент времени; 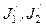 и
и 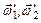 – в момент времени, принятый за конечный.
– в момент времени, принятый за конечный.
· Кинетическая энергия вращающегося тела:
 .
.
Примеры решения задач
Задача №1
Зависимость пройденного телом пути от времени имеет вид 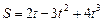 . Определите силу, действующую на тело с массой m=1 кг в конце второй секунды.
. Определите силу, действующую на тело с массой m=1 кг в конце второй секунды.
Решение
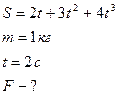 Сила, действующая на тело, по второму закону Ньютона равна:
Сила, действующая на тело, по второму закону Ньютона равна:

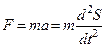 .
.
Мгновенное значение ускорения а определяется первой
производной от скорости по времени или второй производной от пути по
времени:
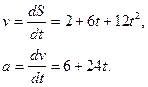
При t=2 с 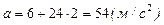 . Тогда
. Тогда 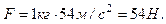
Задача №2
Тело массой 2 кг под действием постоянной силы движется прямолинейно так, что зависимость пройденного пути от времени выражается уравнением S=2t2+3t+1. Определите работу силы за 10 с сначала ее действия.
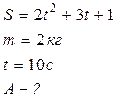 Решение
Решение
 Работа, совершаемая силой, выражается через интеграл:
Работа, совершаемая силой, выражается через интеграл:
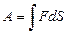 . (1)
. (1)
Сила, действующая на тело, по второму закону Ньютона:
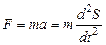 . (2)
. (2)
Мгновенное значение ускорения определяется первой производной от скорости по времени или второй производной пути по времени. В соответствии с этим получим:
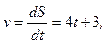 (3)
(3)
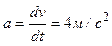 , (4)
, (4)
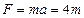 . (5)
. (5)
Тогда из формулы (3) имеем
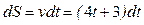 (6)
(6)
Подставив (5) и (6) в уравнение (1), получим:
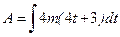
Работа, совершаемая силой за 10 с сначала движения, составит:
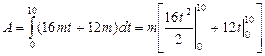
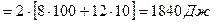 .
.
Задача №3
Диск радиусом R=10 см вращается так, что зависимость угла поворота диска от времени задается уравнением 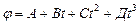
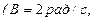
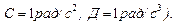 Определите для точек на ободе диска к концу второй секунды после начала движения:
Определите для точек на ободе диска к концу второй секунды после начала движения:
1) тангенциальное ускорение 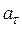 ;
;
2) нормальное ускорение 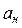 ;
;
3) полное ускорение 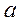 .
.
Решение
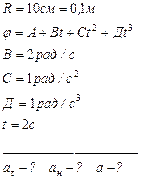 Найдем угловую скорость, взяв производную по времени от заданного уравнения:
Найдем угловую скорость, взяв производную по времени от заданного уравнения:
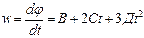 , при
, при 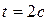
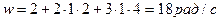 .
.
Угловое ускорение: 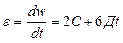 , при
, при 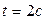
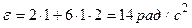 .
.
Тангенциальное ускорение:
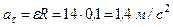 .
.
Нормальное ускорение: 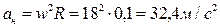 .
.
Полное ускорение: 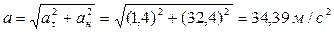 .
.
Задача №4
Шар радиусом R=10 см и массой m=15 кг вращается вокруг оси симметрии согласно уравнению 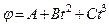
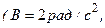 С = –0,2 рад/с3). Определите момент силы М для t=3 c.
С = –0,2 рад/с3). Определите момент силы М для t=3 c.
Решение
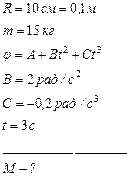 Момент силы согласно уравнению динамики вращательного движения:
Момент силы согласно уравнению динамики вращательного движения:

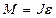 , (1)
, (1)
где J – момент инерции шара,
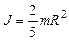 . (2)
. (2)
Угловое ускорение определяется первой производной от угловой скорости по времени или второй производной от угла поворота по времени:
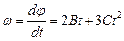 ,
,
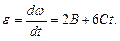 (3)
(3)
Подставив (2) и (3) в (1), получим:
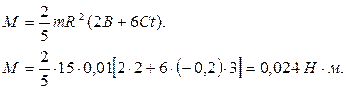
Задача №5
По горизонтальной поверхности катится диск со скоростью 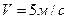 . Определите коэффициент сопротивления, если диск, будучи предоставленный самому себе, остановится, пройдя путь
. Определите коэффициент сопротивления, если диск, будучи предоставленный самому себе, остановится, пройдя путь 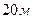 .
.
Решение
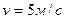 Кинетическая энергия диска:
Кинетическая энергия диска:
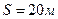
__________ 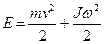 , (1)
, (1)
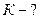 где
где 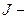 момент инерции диска,
момент инерции диска, 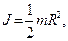
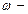 угловая скорость,
угловая скорость, 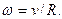
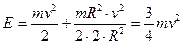 . (2)
. (2)
Эта энергия пойдет на работу по преодоления сил сопротивления 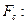
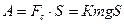 (3)
(3)
Приравнивая (2) и (3), получим:
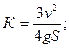
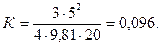
Задача №6
Радиус Луны 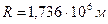 , а ее средняя плотность
, а ее средняя плотность 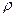
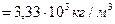 . Определите ускорение свободного падения на поверхности планеты.
. Определите ускорение свободного падения на поверхности планеты.
Решение
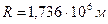 На всякое тело, расположенное вблизи
На всякое тело, расположенное вблизи
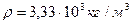 поверхности планеты действует сила тяжести:
поверхности планеты действует сила тяжести:
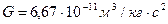
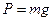 (1)
(1)
__________________ Ее можно приравнять к силе гравитационного
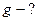 тяготения :
тяготения : 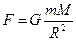 . (2)
. (2)
Откуда 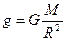 , (3)
, (3)
где 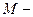 масса Луны,
масса Луны, 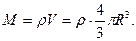 (4)
(4)
Подставив (4) в (3), получим: 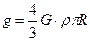 , (5)
, (5)
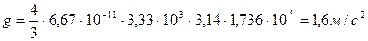 .
.
Задача №7
Логарифмический декремент затухания камертона,  колеблющегося с частотой
колеблющегося с частотой 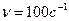 , равен
, равен 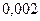 . Через какой промежуток времени амплитуда колебаний возбужденного камертона уменьшится в
. Через какой промежуток времени амплитуда колебаний возбужденного камертона уменьшится в 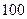 раз? Как изменится при этом энергия колебаний?
раз? Как изменится при этом энергия колебаний?
Решение
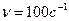 Амплитуда затухающих колебаний изменяется со временем
Амплитуда затухающих колебаний изменяется со временем
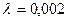 по закону:
по закону: 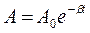 , (1)
, (1)
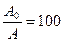 где
где 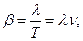
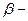 коэффициент затухания,
коэффициент затухания,
_________ 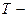 период колебаний,
период колебаний, 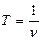 ,
,
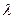 - логарифмический декремент затухания.
- логарифмический декремент затухания.
1) 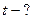 С учетом этого формулу (1) можно записать так:
С учетом этого формулу (1) можно записать так:
2) 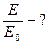
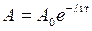 . (2)
. (2)
Откуда 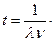
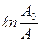 . (3)
. (3)
Энергия колебаний пропорциональна квадрату, произведения амплитуды и частоте колебаний: 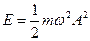 . (4)
. (4)
В данной задаче 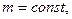
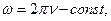 поэтому
поэтому 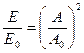 . (5)
. (5)
Проведем вычисления: 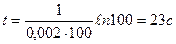 .
.
ЗАДАНИЕ 2. Молекулярная физика и термодинамика
Основные формулы
· Количество вещества однородного газа (в молях):
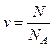 , или
, или 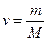 ,
,
где N – число молекул газа; NA – число Авогадро; m – масса газа; М– молярная масса газа.
· Уравнение Клапейрона-Менделеева (уравнение состояния газа):
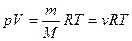 ,
,
где p – давление газа; V – его объем; T – температура; R – молярная газовая постоянная.
· Масса молекулы mi:
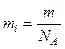
· Концентрация молекул (число молекул в единице объема) n0:
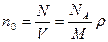 ,
,
где N – число молекул, содержащихся в данном объеме; r – плотность вещества.
· Средняя кинетическая энергия движения молекулы:
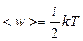 ,
,
где i - число степеней свободы; k - постоянная Больцмана.
· Основное уравнение кинетической теории газов:
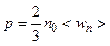 ,
, 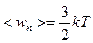 ,
,
где n0 – концентрация молекул; <wп> – средняя кинетическая энергия поступательного движения молекул.
· Зависимость давления газа от концентрации молекул n0 и температуры Т:
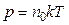 .
.
· Средняя квадратичная скорость молекулы:
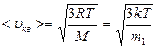 .
.
· Средняя арифметическая скорость молекулы:
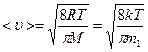 .
.
· Наиболее вероятная скорость молекулы:
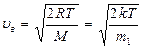 ,
,
где m1 – масса одной молекулы.
· Удельная теплоемкость газа при постоянном объеме (сv) и при постоянном давлении (ср):
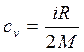 ;
; 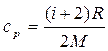 .
.
· Связь между удельной (с) и молярной (С) теплоемкостями:
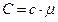 .
.
· Уравнение Роберта Майера:
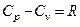 .
.
· Среднее число соударений молекул:
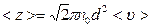 ,
,
где d – эффективный диаметр молекулы.
· Средняя длина свободного пробега молекулы:
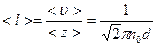 .
.
· Масса, переносимая при диффузии сквозь площадку DS за промежуток времени Dt (закон Фика):
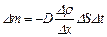 ,
,
где D – коэффициент диффузии; Dr /Dх – градиент плотности.
· Энергия, переносимая вследствие теплопроводности через площадку DS за промежуток времени Dt (закон Фурье):
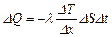 ,
,
где l – коэффициент теплопроводности; 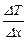 – градиент температуры.
– градиент температуры.
· Сила внутреннего трения F, действующая между слоями жидкости, пропорциональна площадке соприкасающихся двух слоев жидкости DS, градиенту скорости 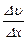 и коэффициенту внутреннего трения h (закон Ньютона):
и коэффициенту внутреннего трения h (закон Ньютона):
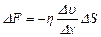 .
.
· Внутренняя энергия газа:
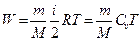 .
.
· Первое начало термодинамики:
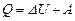 ,
,
где Q – теплота, сообщенная системе (газу); DU – изменение внутренней энергии системы; А – работа, совершаемая системой против внешних сил.
· Работа расширения газа:
а) при изобарном процессе: 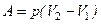 =
= 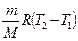 ;
;
б) при изотермическом процессе:
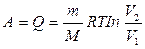 =
= 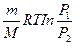
в) при адиабатном процессе:
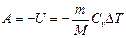 .
.
· Уравнение Пуассона для адиабатного процесса:
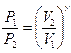 ,
, 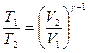 и
и 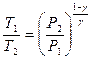
· Термический КПД идеальной тепловой машины:
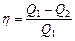 , или
, или 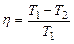 ,
,
где Q1 – теплота, полученная рабочим телом от нагревателя; Q2 – теплота, переданная рабочим телом охладителю; Т1 и Т2 – термодинамические температуры нагревателя и охладителя.
· Коэффициент поверхностного натяжения:
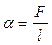 ,
,
где F – сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости.
· Высота подъема жидкости в капиллярной трубке:
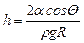 ,
,
где Q - краевой угол; r - плотность жидкости; R – радиус трубки.
· Изменение энтропии системы при переходе из состояния А в состояние В: 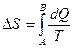 ,
,
где 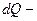 количество теплоты, переданное системой ; Т- температура, при которой происходила теплопередача.
количество теплоты, переданное системой ; Т- температура, при которой происходила теплопередача.
Примеры решения задач
Задача №1
Определить среднюю кинетическую энергию молекулы кислорода, находящейся при температуре 17°С. Найти также кинетическую энергию вращательного движения всех молекул, содержащихся в 4 г кислорода.
Решение
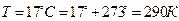 Средняя кинетическая энергия (поступательного
Средняя кинетическая энергия (поступательного
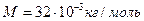 и вращательного движения) одной молекулы:
и вращательного движения) одной молекулы:
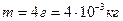
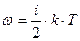 (1)
(1)
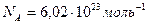 где
где 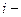 число степеней свободы, двухатомного
число степеней свободы, двухатомного
_____________________ газа 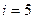 (
( 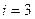 на поступательное движение и
на поступательное движение и 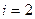
на вращательное движение) ; 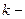 постоянная
постоянная
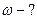
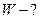 Больцмана,
Больцмана, 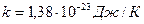 .
.
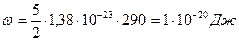 .
.
Кинетическая энергия вращательного движения всех молекул газа:
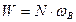 , (2)
, (2)
где 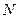 – число молекул:
– число молекул: 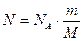 (3)
(3)
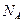
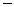 число Авогадро;
число Авогадро;
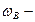 кинетическая энергия вращательного движения:
кинетическая энергия вращательного движения:
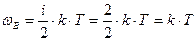 . (4)
. (4)
Подставив (3) и (4) в (2), получим: 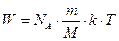 .
.
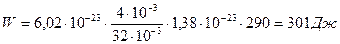 .
.
Задача №2
Азот массой m нагревается в одном случае изобарно, а в другом изохорно на DТ. Во сколько раз потребуется больше теплоты в первом случае, чем во втором?
Решение
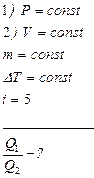 Теплота, потребляемая при изобарном процессе (P=const):
Теплота, потребляемая при изобарном процессе (P=const):
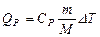 . (1) Теплота, потребляемая при изохорном процессе (V=const):
. (1) Теплота, потребляемая при изохорном процессе (V=const):
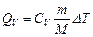 , (2)
, (2)
где СP и CV – молярные теплоемкости при постоянном давлении и объеме соответственно.
Поделив (1) на (2), получим:
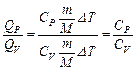 . (3)
. (3)
Так как
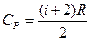 , (4)
, (4)
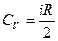 , (5)
, (5)
то подставив (4) и (5) в (3), получим:
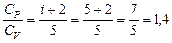 .
.
Таким образом, для любой массы газа при одинаковой разности температур отношения теплот есть величина постоянная.
Задача №3
Определите диаметр молекулы кислорода, если известно, что для кислорода коэффициент внутреннего трения при нормальных условиях равен 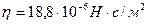 .
.
Решение
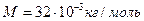 Коэффициент внутреннего трения:
Коэффициент внутреннего трения:
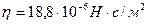
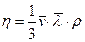 , (1)
, (1)
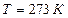
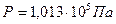 где
где 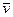 - средняя арифметическая скорость;
- средняя арифметическая скорость;
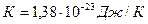
_________________ 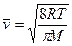 , (2)
, (2)
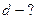
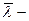 средняя длина свободного пробега молекулы
средняя длина свободного пробега молекулы
кислорода:
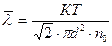 , (3)
, (3)
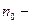 концентрация молекул:
концентрация молекул: 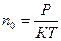 , (4)
, (4)
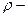 плотность кислорода:
плотность кислорода: 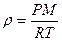 . (5)
. (5)
Подставив (2),(3),(4),(5) в уравнение (1), получим:
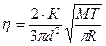 , откуда
, откуда 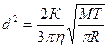 ,
,
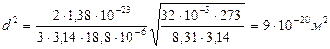 ,
, 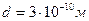 .
.
Задача №4
1 кг водорода нагрели до температуры 100°С в условиях свободного расширения (P=const). Определите: 1) количество теплоты, сообщенное газу; 2) изменение его внутренней энергии; 3) работу расширения.
Решение
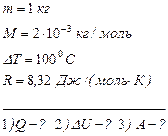 1) Количество теплоты Q, сообщенное водороду при P=const, определим по формуле:
1) Количество теплоты Q, сообщенное водороду при P=const, определим по формуле:
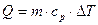 , (1)
, (1)
где ср – удельная теплоемкость газа при P=const.
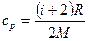 , (2)
, (2)
где i – число степеней свободы, для двухатомного газа i=5. Подставив (2) в (1), получим: 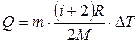 .
.
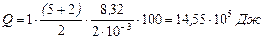 .
.
2) Внутренняя энергия газа выражается формулой:
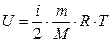 ,
,
а изменение внутренней энергии:
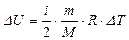 , (3)
, (3)
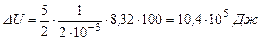 .
.
3) Работу расширения газа определим по формуле, выражающей первое начало термодинамики:
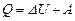 . (4)
. (4)
Откуда 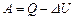 ,
,
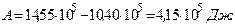 .
.
Задача№5
Азот, находящийся при температуре 27°С и давлении в 1,5 атм, был адиабатически сжат до объема в 5 раз меньше начального объема. Определите давление и температуру азота после его сжатия.
Решение
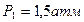 Давление после сжатия определим по формуле
Давление после сжатия определим по формуле
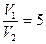 Пуассона:
Пуассона:
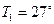
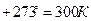
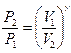 , откуда
, откуда 
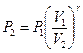 , (1)
, (1)
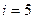 где
где 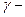 отношение теплоемкостей при постоянном
отношение теплоемкостей при постоянном
_________________ давлении и при постоянном объеме:
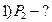
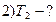
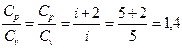 , (2)
, (2)
где 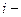 число степеней свободы,
число степеней свободы,
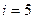 для двухатомного газа.
для двухатомного газа.
Температуру 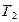 - после сжатия определим из формулы:
- после сжатия определим из формулы:
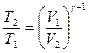 , откуда
, откуда 
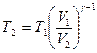 .
.
Произведем вычисления: 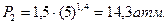
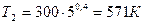 .
.
ЗАДАНИЕ 3. Электростатика и постоянный ток
Основные формулы
По закону Кулона сила взаимодействия F между точечными зарядами Q1 и Q2, находящимися на расстоянии r один от другого в среде с диэлектрической проницаемостью e,
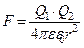 ,
,
где e0 = 8,85 10-12 Ф/м – электрическая постоянная.
· Напряженность электрического поля:
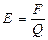 ,
,
где F – сила, с которой поле действует на пробный заряд Q.
· Напряженность поля точечного заряда Q, или поля вне равномерного заряженного шара:
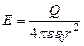 ,
,
где r – расстояние от заряда Q или от центра шара до точки, в которой определяется напряженность.
· Напряженность поля прямолинейной равномерно заряженной бесконечно длинной нити:
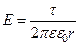 ,
,
где t – линейная плотность заряда нити; r – расстояние от нити до точки, в которой определяется напряженность поля.
· Напряженность поля, образованного равномерно заряженной бесконечной плоскостью:
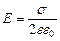 ,
,
где s – поверхностная плотность заряда плоскости.
· Разность потенциалов между двумя точками электрического поля определяется работой, совершаемой при перемещении единичного положительного заряда из одной точки плоя в другую:
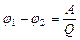 ,
,
где А – работа перемещения заряда Q.
· Потенциал поля точечного заряда:
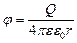 ,
,
где r – расстояние от заряда Q, создающего поле, до точки, в которой определяется потенциал.
· Для плоского конденсатора связь между напряженностью поля Е и разностью потенциалов U его пластин:
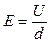 ,
,
где d – расстояние между пластинами.
· Электроемкость уединенного проводника:
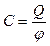 .
.
· Емкость плоского конденсатора:
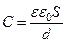 ,
,
где S - площадь пластины конденсатора.
· Емкость уединенного проводящего шара:
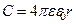 ,
,
где r – радиус шара.
· Емкость С системы конденсаторов связана с емкостями Сi, входящих в нее конденсаторов, соотношениями:
а) при последовательном соединении:
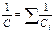 , или
, или 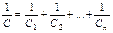 ;
;
б) при параллельном соединении:
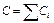 , или
, или 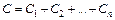
· Энергию W уединенного заряженного проводника можно определить по следующим формулам:
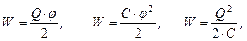
где Q, j и С – соответственно заряд, потенциал и емкость проводника.
Для плоского конденсатора
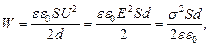
где S – площадь пластины; U – разность потенциалов между пластинами; s – поверхностная плотность заряда пластины; Е – напряженность электрического поля конденсатора.
· Плотность энергии электрического поля:
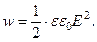
· Сила постоянного тока I связана с количеством электричества Q, проходящим через поперечное сечение проводника за время t, следующим соотношением:
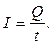
· Плотность тока:
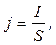
где S – площадь поперечного сечения проводника.
· Сопротивление проводника длиной l и площадью поперечного сечения S:
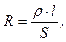
где r – удельное сопротивление материала проводника.
· Закон Ома для участка цепи:
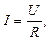
где U – разность потенциалов на концах участка; R – его сопротивление.
· Закон Ома для полной цепи:
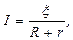
где x – электродвижущая сила источника тока; R – внешнее сопротивление цепи, r – внутреннее сопротивление источника тока.
· Удельное сопротивление r проводника связано с температурой t соотношением:
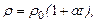
где r0 – удельное сопротивление при 0°С; a – температурный коэффициент сопротивления.
· Работа тока А на участке цепи (или количество теплоты, выделенное в нем при прохождении тока) определяется формулами:
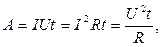
где t – время прохождения тока.
· Мощность тока, выделяемая на участке цепи, определяется соотношением:
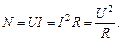
· Полная мощность, выделяемая в цепи:
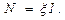
· Для расчета разветвленных цепей применяются два правила Кирхгофа.
Первое правило для алгебраической суммы токов в узле:
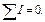
Второе правило для алгебраической суммы произведений токов на сопротивление участков и алгебраической суммы электродвижущих сил в контуре:
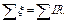
· Масса m вещества, выделившегося на электроде, пропорциональна химическому эквиваленту А/n, силе тока, протекающего через электролит, и времени прохождения тока:
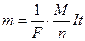 ,
,
где F – число Фарадея,
М – молярная масса,
n - валентность.
Примеры решения задач
Задача №1
Два заряда Q1 = +8 нКл и Q2 = -6 нКл находятся в воздухе на расстоянии d = 8 см друг от друга. Определить напряженность и потенциал электрического поля в точке А, находящейся на расстоянии 10 см от каждого заряда.
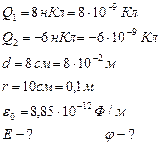 Решение
Решение


Напряженность электрического поля в точке А равна геометрической сумме напряженностей 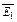 и
и 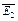 , создаваемых зарядами Q1 и Q2.
, создаваемых зарядами Q1 и Q2.
Модуль результирующей напряженности Е по теореме косинусов определяется как диагональ параллелограмма, построенного на векторах 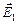 и
и 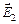 :
:
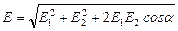 (1)
(1)
Абсолютные значения напряженностей и cosa определяем по формулам:
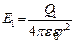 ,
, 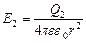 (2)
(2)
По теореме косинусов:
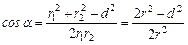 (3)
(3)
Подставив (2) и (3) в (1), получим:
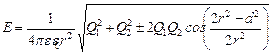 .
.
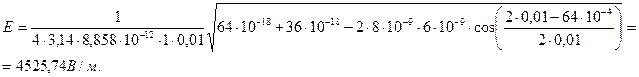
Потенциал электрического поля в точке А равен алгебраической сумме потенциалов j1 и j2 полей, создаваемых зарядами Q1 и Q2:
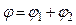 (4)
(4)
Потенциал поля точечного заряда
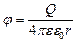 (5)
(5)
Подставив (5) в (4), получим:
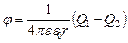 (6)
(6)
Вычислим:
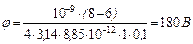 .
.
Задача №2
На помещенный между обкладками конденсатора заряд Q=2,5 нКл действует сила F=50 мкН. Площадь каждой пластины 100 см2, расстояние между пластинами d=3 см. определить: 1) емкость конденсатора; 2) напряженность между обкладками; 3) разность потенциалов между обкладками; 4) энергию конденсатора; 5) объемную плотность энергии.
Решение
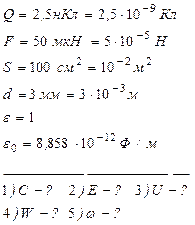 1) Емкость конденсатора:
1) Емкость конденсатора:
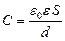 (1)
(1)
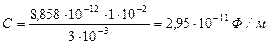
2) Напряженность между обкладками:
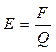 (2)
(2)
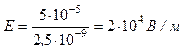 3) Разность потенциалов:
3) Разность потенциалов:
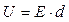 (3)
(3)
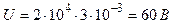
4) Энергия конденсатора:
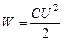 (4)
(4)
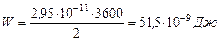 .
.
5) Объемная плотность энергии:
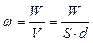 . (5)
. (5)
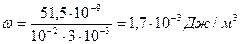 .
.
Задача №3
Сколько времени потребуется для нагревания воды массой 1,0 кг от начальной температуры 100 С до кипячения в электрическом чайнике с нагревателем мощностью 800 Вт, если его КПД равен 90%? Какова сила тока в электрической спирали, если напряжение в сети 220 В.
m=1,0 кг Решение
t1 = 100C 1) Количество теплоты, необходимой для нагревания
t2 = 1000C воды: Q = cm(t2-t1)=cmΔ t .(1)
N = 800 Bт Она связана с мощностью нагревателя:
с = 4,2*10 3 Дж/кг*К Q=ηN t (2)
η = 90 % = 0,9 Приравняв (1) и (2), получим:
____________________ 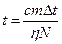 ,
,
1) t = ? 2) I = ? 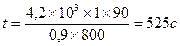 .
.
2) Сила тока: 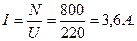
Задача№4
Внутреннее сопротивление аккумулятора 1 Ом. При силе тока 0,5 А его КПД равен 0,8. Определите ЭДС аккумулятора.
Решение
r=1Ом КПД источника тока: 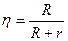 . (1)
. (1)
J=0,5А Отсюда 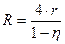 . (2)
. (2)
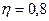 Закон Ома для замкнутой цепи:
Закон Ома для замкнутой цепи: 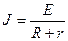 (3)
(3)
___________ Подставив (2) в (1), получим:
Е - ? 
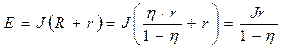 ;
; 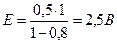
Задача№5
Два одинаковых источника тока соединены в одном случае последовательно, в другом параллельно и замкнуты на внешнее сопротивление 10 Oм. При каком внутреннем сопротивлении источника сила тока во внешней цепи будет в обоих случаях одинаковой?
Решение
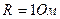 При последовательном соединении
При последовательном соединении 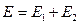 ,
,
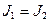 а внутреннее сопротивление
а внутреннее сопротивление 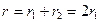 .
.
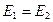 По закону Ома:
По закону Ома: 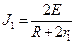
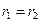
________ При параллельном соединении 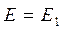 ,
,
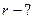 а внутреннее сопротивление
а внутреннее сопротивление 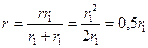
По закону Ома: 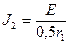
По условию 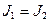 или
или 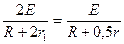 ;
; 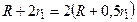 ,
, 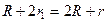 ,
,
Отсюда 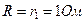 .
.
ЗАДАНИЕ 4. Электромагнетизм и переменный ток
Основные формулы
· Связь между индукцией и напряженностью магнитного поля:
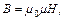
где m0 – магнитная постоянная, m0 = 4p*10-7 Гн/м,
m – относительная магнитная проницаемость среды.
· Закон Био-Савара-Лапласа:
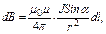
где dB – магнитная индукция поля, создаваемая элементом проводника длиной dl с током J; r – радиус-вектор, направленный от элемента проводника к точке, в которой вычисляется магнитная индукция; a - угол между радиус-вектором и направлением тока в элементе проводника.
· Магнитная индукция в центре кругового тока:
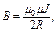
где R – радиус кругового витка.
· Магнитная индукция поля прямого тока:
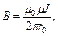
где r0 – расстояние от оси проводника до точки, в которой вычисляется магнитная индукция.
· Магнитная индукция поля, создаваемая отрезком провода с током J:
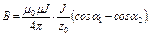
где a1 и a2 – углы между направлением тока и радиус – вектора, проведенные из начала и конца проводника в рассматриваемую точку.
· Напряженность магнитного поля внутри соленоида:
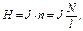
где п – число витков на единицу длины соленоида, N – общее число витков,
L – длина соленоида.
· Поток магнитной индукции, связанной с контуром:
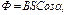
где S – площадь, ограниченная контуром, a – угол между нормалью к плоскости контура и направлением вектора магнитной индукции.
· На прямолинейный проводник длиной l c током J, находящийся в магнитном поле, действует сила Ампера:
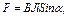
где a – угол между направлениями тока и вектора индукции.
· На заряженную частицу, движущуюся со скоростью n в магнитном потоке, действует сила Лоренца:
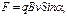
где q - заряд частицы, a - угол между направлением поля и скоростью частицы.
· При перемещении проводника с током J в магнитном поле (перпендикулярно полю) совершается работа:
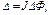
где DФ – магнитный поток через площадь, описываемую проводником при перемещении.
· Закон Фарадея для электродвижущей силы индукции:
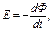
где 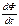 – скорость изменения магнитного потока через площадь, ограниченную кругом.
– скорость изменения магнитного потока через площадь, ограниченную кругом.
· Возникающая в контуре ЭДС самоиндукции:
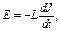
где L – индуктивность в контуре, 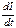 – скорость изменения тока в контуре.
– скорость изменения тока в контуре.
· Индуктивность соленоида:
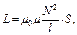
где N – число витков, S – площадь поперечного сечения соленоида, l – длина соленоида.
Индуктивность контура L связана с пронизывающим его магнитным потоком Ф следующим соотношением:
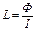 ,
,
где I – ток в контуре, обуславливающий магнитный поток.
Энергия магнитного поля, создаваемого током I в контуре и индуктивностью L:
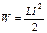 .
.
· Плотность энергии магнитного поля:
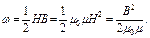
где Н – напряженность, В – индукция магнитного поля.
ЭДС индукции, возникающая в рамке площадью S, содержащей N витков, при вращении ее с угловой скоростью w в магнитном поле с индукцией В определяется соотношением:
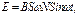
где wt – угол поворота рамки к моменту времени t.
Период собственных колебаний в контуре, не содержащих омическое сопротивление (ф.Томсона):
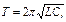
Полное сопротивление цепи переменного тока, содержащей последовательно соединенные омическое сопротивление R0, индуктивность L и емкость:
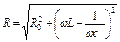 .
.
Примеры решения задач.
Задача №1
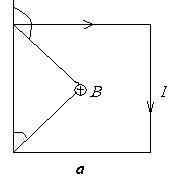 Определите индукцию магнитного поля в центре проволочной квадратной рамки со стороной = 20 см, если по рамке течет ток 3А.
Определите индукцию магнитного поля в центре проволочной квадратной рамки со стороной = 20 см, если по рамке течет ток 3А.
Решение
= 20 см=0,2 м Индукция магнитного поля в центре
I = 3A рамки равна векторной сумме ______________ индукций магнитного поля,
B -? создаваемых всеми её сторонами
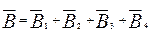 .
.
Все эти факторы направлены в одну сторону перпендикулярно к плоскости рамки и вследствие симметрии B = 4Bj
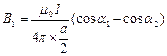 , где 1 = 45º , 2 = 180º - 45º = 135º
, где 1 = 45º , 2 = 180º - 45º = 135º
Окончательно имеем: 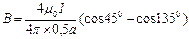
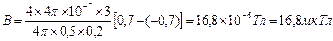
Задача №2
Катушка длиной l = 40 см и диаметром 5 см содержит 300 витков. По катушке течет ток I = 1A. Определите: 1) индуктивность катушки; 2) магнитный поток, пронизывающий площадь её поперечного сечения.
Решение
l=40 cм=0,4м 1) Индуктивность соленоида:
d=5cм=5*10-2м L=μ0 μ 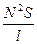 (1)
(1)
N=300 витков Площадь поперечного сечения:
I=1A 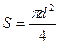 (2)
(2)
μ0=4π*10-7Гн/м С учетом (2) индуктивность:
_________________ 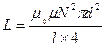 (3)
(3)
1) L-? 2)Ф - ? 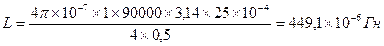
2) Магнитный поток: 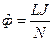 , (4)
, (4)
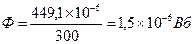 .
.
Задача №3
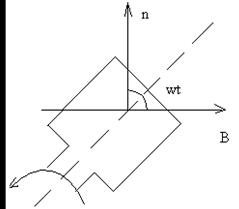
В однородном магнитном поле с индукцией В = 0,1 Тл равномерно с частотой n = 600 мин-1 вращается рамка, содержащая 1000 витков, плотно прилегающих друг к другу. Площадь рамки 200 см2. Ось вращения лежит в плоскости рамки и перпендикулярна направлению магнитной индукции. Определите максимальную ЭДС, индуцируемую в рамке.
Решение
B = 0,1 Тл
n = 600 об/мин=10 об/с
N = 1000 витков
S = 200 см2=2*10-2м2
_________________
E max - ?
ЭДС по закону Фарадея: 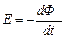
Ф=NBS cos, = ωt = 2πnt
Окончательно имеем: 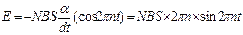 . Emax – при sin 2πnt.
. Emax – при sin 2πnt.
Emax=2πnNBS=6.28*10*1000*0.1*2*10-2=125B
Задача №4
По обмотке соленоида индуктивностью L = 3 мГн, находящегося в диамагнитной среде, течет ток I = 0,4 А. Площадь поперечного сечения S = 10 см2 и число витков N = 1000. Определить внутри соленоида: 1)энергию магнитного поля; 2) магнитную индукцию.
Решение
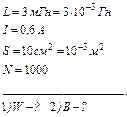 1) Энергия магнитного поля:
1) Энергия магнитного поля: 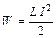 (1)
(1) 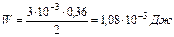
2) Индукция магнитного поля соленоида: 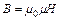 , (2)
, (2)
где Н – напряженность магнитного поля.
Зная индуктивность, можно определить магнитную
проницаемость: 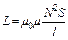 ,
,
откуда 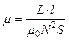 , (3)
, (3)
где l – длина соленоида.
Напряженность магнитного поля: 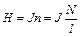 (4)
(4)
Подставив (4) и (3) в (2), получим: 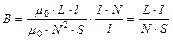 (5)
(5)