Потенциальная энергия упругой деформации

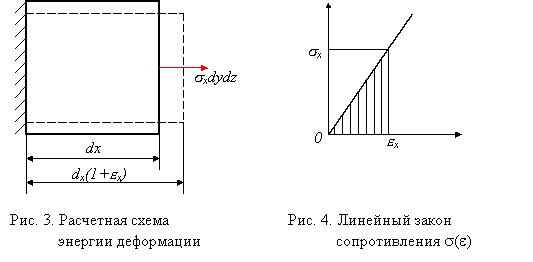
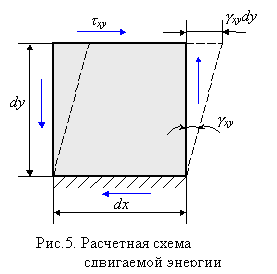
Рассмотрим вначале элементарный объем dV=dxdydz в условиях одноосного напряженного состояния (рис. 1). Мысленно закрепим площадку х=0 (рис. 3). На противоположную площадку действует сила s_xdydz. Эта сила совершает работу на перемещении e_xdx. При увеличении напряжения от нулевого уровня до значения s_x соответствующая деформация в силу закона Гука также увеличивается от нуля до значения e_x, а работа пропорциональна заштрихованной на рис. 4 площади: dA=0,5s_xe_xdV. Если пренебречь кинетической энергией и потерями, связанными с тепловыми, электромагнитными и другими явлениями, то в силу закона сохранения энергии совершаемая работа перейдет в потенциальную энергию, накапливаемую в процессе деформирования: dA=dU=0,5s_xe_xdV. Величина Ф=dU/dV называется удельной потенциальной энергией деформации, имеющей смысл потенциальной энергии, накопленной в единице объема тела. В случае одноосного напряженного состояния

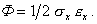
При одновременном действии напряжений s_x, s_y и s_z на главных площадках (т. е. при отсутствии касательных напряжений) потенциальная энергия равна сумме работ, совершаемых силами s_xdydz, s_ydxdz, s_zdxdy на соответствующих перемещениях e_xdx, e_ydy, e_zdz. Удельная потенциальная энергия равна

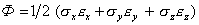
(2.47)

В частном случае чистого сдвига в плоскости Оху, изображенном на рис. 5, сила t_xydxdz совершает работу на перемещении g_xydy. Соответствующая этому случаю удельная потенциальная энергия деформации равна

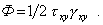
Подобные соотношения будут иметь место при сдвиге в других плоскостях.

В общем случае напряженно-деформированного состояния будем иметь

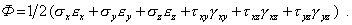
(11)

Если деформации выразить через напряжения с помощью соотношений упругости (5) и (6), то получим эквивалентную форму записи через компоненты тензора напряжений

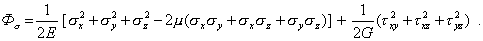
(12)

Выразив напряжения через деформации с использованием соотношений (6) и (10), получим еще одну форму записи для Ф - через компоненты тензора деформаций

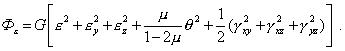
Еще одну форму записи для удельной потенциальной энергии деформации получим, разложив тензоры напряжений и деформаций на шаровые тензоры и девиаторы. В результате (11) можно привести к одной из форм

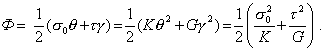
(13)

Здесь введены обозначения для t - интенсивности касательных напряжений и g - интенсивности деформаций сдвига, которые выражаются через вторые инварианты J₂(ds) и J₂(de) девиаторов тензора напряжений и тензора деформаций следующим образом:

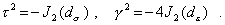
Первые слагаемые в (13) соответствуют произведению шаровых составляющих тензоров напряжений и деформаций, а вторые - произведению девиаторных составляющих. Так как шаровой тензор характеризует изменение объема, а девиатор - изменение формы, то соотношения (13) можно интерпретировать как разложение удельной потенциальной энергии на две составляющие: Ф=Ф₀ + Ф_ф, где Ф₀ соответствует изменению объема без изменения формы, а Ф_ф - изменению формы без изменения объема. Первая составляющая будет вычисляться через компоненты тензора напряжений следующим образом:

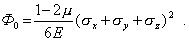
(14)

Удельную потенциальную энергию изменения формы проще найти не через интенсивность касательных напряжений, а как разность Ф - Ф₀. Вычитая (14) из (12), после преобразований получим

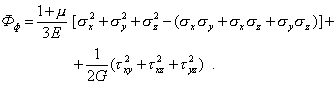
9 Механические характеристики конструкционных материалов

Ключевые слова: упругое состояние; пластичное состояние; пределы пропорциональности, упругости, текучести, прочности.

Механические характеристики определяются следующими факторами:

• веществом, его структурой и свойствами;
• конструктивными особенностями элемента, т. е, размерами, формой, наличием концентраторов, состоянием поверхности;
• условиями при нагружении: температурой, скоростью, повторяемостью нагрузки и др.

Конструкционные материалы в процессе деформирования вплоть до разрушения ведут себя по разному. Пластичное поведение характеризуется существенным изменением формы и размеров, при этом к моменту разрушения развиваются значительные деформации, не исчезающие после снятия нагрузки. Такие материалы называют пластичными. При хрупком поведении разрушение наступает при весьма малых деформациях, и материалы с такими свойствами называют хрупкими. Однако одни и те же конструкционные материалы, находящиеся в различных условиях деформирования, ведут себя по разному: при одних условиях проявляют себя как пластичные материалы, при других - как хрупкие. В связи с этим, основные макромеханические характеристики материалов - упругость, пластичность, вязкость и др. правильнее относить не к их свойствам, а к состояниям материала.