Замыкающие соотношения

Для полного замыкания системы уравнений фильтрационного течения необходимо знание зависимостей r,m,k,μ от давления.

Зависимость плотности от давления

Различают жидкости:

а) Несжимаемую – r=соnst. (2.49)

в) Упругую, имеющую место при нестационарных процессах за счёт расширения объёма нефти и воды при снижении давления

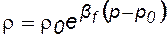, (2.50)

где 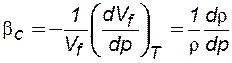– коэффициент объёмного расширения жидкости, V_с – объём жидкости;

b_с=(7–30)10^-10 Па^-1 – для нефти и (2,7–5)10^-10Па^-1 – для пластовой воды.

с) Сжимаемую – газ. До р_пл < 9 МПа и D р < 1 МПа можно использовать уравнение состояния совершенного газа

р=r R T,(2.51)

где R – газовая постоянная.

Совершенный газ – это газ, молекулы которого не имеют объёма и не взаимодействуют между собой.

При изотермическом процессе (Т=const) используют соотношение

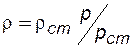. (2.52)

Если р_пл > 9 МПа, то надо использовать обобщённое уравнение состояния реального газа

р=zr R T (2.53)

или двузпараметрические уравнения состояния, типа Редлиха – Квонга.

В уравнении (2.53): z – коэффициент сверхсжимаемости, являющийся функцией давления при изотермическом течении.

Зависимость вязкости от давления

При давлениях меньше давления насыщения можно считать, что вязкость не зависит от давления, а при больших значениях давления

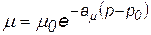. (2.54)

Зависимость пористости от давления

Пористость связана, в первую очередь, с давлением между частицами пористой среды – эффективным давлением s_эф, передающимся через поверхности контакта зёрен породы. Считается, что

s_эф + р_пл = р_горн = const. (2.55)

Здесь р_пл– пластовое давление; р_горн= r_горн g H –горное давление, возникающее под действием масс горных пород над кровлей пласта средней плотности r_горн; Н – глубина залегания пласта.

При разработке р_пл падает и, согласно (2.55), растёт s_эф.Увеличение s_эф приводит к деформации пласта, а именно, переупаковке зёрен в сторону уплотнения и даже их разрушения. Принимается, что

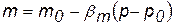, (2.56)

где b_т – коэффициент объёмной упругости породы с пределами изменения (0,3 – 2)10^-10Па^-1.

Зависимость проницаемости от давления

В связи с уменьшением пористости при увеличении давления, также по аналогичному закону уменьшается проницаемость

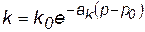. (2.57)

При D р < 10 МПа показатель в (2.27, 2.33 –2.34) меньше 1 и, следовательно, данные экспоненциальные зависимости можно разложить в ряд Тейлора. Ограничиваясь первыми двумя членами, получаем

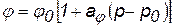, (2.58)

где j– общее обозначение вышеприведённых параметров.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1.Скорость фильтрации, физический смысл и связь с истинной скоростью.

2.Уравнение неразрывности. Его физический смысл.

3.Уравнение сохранения количества движения.

4.Объяснение закона Дарси из общего уравнения сохранения количества движения.

5.Градиент: вид данной функции в декартовой системе координат и объяснение составляющих данного представления, тип (векторный или скалярный), тип аргумента (векторный или скалярный).

6.Дивергенция: вид данной функции в декартовой системе координат и объяснение составляющих данного представления, тип (векторный или скалярный), тип аргумента (векторный или скалярный).

7.Вид закона Дарси.

8.Коэффициент фильтрации, его отличие от коэффициента проницаемости. Связь данных коэффициентов и их размерности.

9.Нижняя граница применимости закона Дарси для пористой среды. Закон фильтрации для нижней области.

10.Верхняя граница применимости закона Дарси для пористой среды. Законы фильтрации для верхней области.

11.Критерии применимости закона Дарси для пористой среды.

12.Верхняя граница применимости закона Дарси для трещинной среды. Критерии применимости закона Дарси для трещинной среды.

13.Связь трещинной проницаемости с раскрытостью трещин и давлением.

14.Что такое потенциальное течение?

15.Потенциал поля скоростей и выражение для закона Дарси через потенциал.

16.Вывод основного уравнения потенциального фильтрационного течения.

17.Оператор Лапласа: вид данной функции в декартовой системе координат, тип (векторный или скалярный), тип аргумента (векторный или скалярный).

18.Свойства уравнения Лапласа.

19.Характерные особенности трещинно-пористой среды.

20.Система дифференциальных уравнений для трещинно-пористой среды.

21.Внешние граничные условия.

22.Внутренние граничные условия.

23.Замыкающие соотношения.

24.Связь пластового давления с эффективным. Что такое эффективное давление?

25.Условие применимости линейного приближения в зависимостях основных параметров от давления.