Криволинейные интегралы
Двойные и тройные интегралы
Двойной интеграл.
п.1 Задачи, приводящие к понятию двойного интеграла.
Обобщением определенного интеграла на случай функций двух переменных является двойной интеграл.
Пусть в замкнутой области  плоскости
плоскости 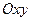 задана положительная непрерывная функция
задана положительная непрерывная функция 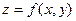 .
.
Определение: Часть пространства, ограниченная снизу замкнутой областью  , сверху поверхностью
, сверху поверхностью 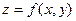 , с боков цилиндрической поверхностью, образующие которой параллельны оси
, с боков цилиндрической поверхностью, образующие которой параллельны оси 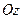 , а направляющий служит контур области
, а направляющий служит контур области  , называется цилиндрическим телом.
, называется цилиндрическим телом.
Найдем объем данного цилиндрического тела.
Разобьем область  на
на 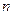 элементарных областей
элементарных областей 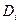 , площадь которых обозначим через
, площадь которых обозначим через 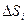 , а диаметры
, а диаметры 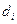
В каждой области 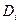 выберем произвольную точку
выберем произвольную точку 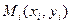 , найдем значение функции в этой точке
, найдем значение функции в этой точке 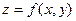 .
.
Рассмотрим цилиндрические столбики с основанием 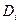 , ограниченные сверху кусками поверхности
, ограниченные сверху кусками поверхности 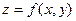 .
.
В своей совокупности они составляют тело 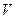 . Объем цилиндрического столбика приближенно равен
. Объем цилиндрического столбика приближенно равен 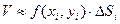 , а объем цилиндрического тела:
, а объем цилиндрического тела: 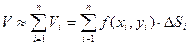 (1)
(1)
Эта сумма называется интегральной суммой функции 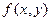 в области
в области  .
.
Равенство (1) тем точнее, чем больше  и чем меньше размеры элементарных областей
и чем меньше размеры элементарных областей  . Если
. Если  неограниченно возрастает, то за объем цилиндрического тела можно будет принять предел интегральной суммы:
неограниченно возрастает, то за объем цилиндрического тела можно будет принять предел интегральной суммы:
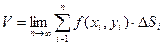
Определение: Если существует 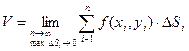 , то он называется двойным интегралом от функции
, то он называется двойным интегралом от функции 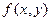 по области
по области  и обозначается
и обозначается 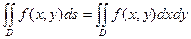 , т.е.
, т.е. 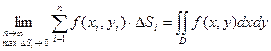 .
.
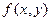 - интегрируемая функция в области
- интегрируемая функция в области  ,
,
 - область интегрирования,
- область интегрирования,
 и
и  - переменные интегрирования,
- переменные интегрирования,
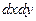 или
или 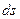 - элемент площади.
- элемент площади.
Для всякой ли функции 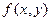 существует двойной интеграл?
существует двойной интеграл?
Теорема 1 (достаточное условие интегрируемости функции)
Если функция 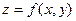 непрерывна в замкнутой области
непрерывна в замкнутой области  , то она интегрируема в этой области.
, то она интегрируема в этой области.
Величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Если при любых 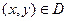
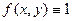 , то
, то 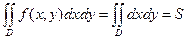 - площадь области
- площадь области  .
.
Рассмотрим задачу на нахождение массы плоской пластинки. Пусть требуется найти массу 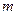 плоской пластинки
плоской пластинки  , зная ее поверхностную плотность
, зная ее поверхностную плотность 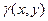 . Функция
. Функция 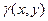 - непрерывна в каждой точке области
- непрерывна в каждой точке области  .
.
Разобьем пластинку  на
на 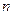 элементарных частей
элементарных частей 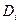 с площадями
с площадями 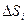 . В каждой области
. В каждой области 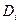 возьмем произвольную точку
возьмем произвольную точку 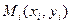 и вычислим в ней плотность
и вычислим в ней плотность 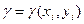 . Если в области
. Если в области 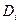 достаточно малы, то плотность можно считать постоянной и равной
достаточно малы, то плотность можно считать постоянной и равной 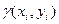 , а массу данной области
, а массу данной области 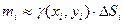 .
.
Тогда масса всей пластинки  будет приближенно равна
будет приближенно равна 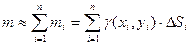 .
.
Точное значение массы пластинки  получим при условии, что
получим при условии, что 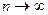 :
: 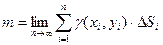 или
или 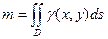 .
.
Итак, двойной интеграл от функции 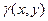 численно равен массе пластинки, если подынтегральную функцию
численно равен массе пластинки, если подынтегральную функцию 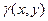 считать плотностью этой пластинки в точке
считать плотностью этой пластинки в точке 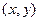 . В этом состоит физический смысл двойного интеграла.
. В этом состоит физический смысл двойного интеграла.
п. 2 Основные свойства двойного интеграла
1. Постоянный множитель 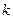 можно вынести за знак двойного интеграла
можно вынести за знак двойного интеграла 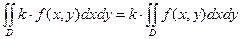 .
.
2. Если функция 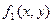 и
и 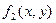 интегрируемы в области
интегрируемы в области  , то
, то 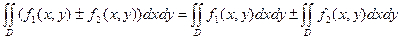 .
.
3. Если область 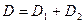 , то
, то 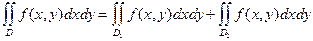 .
.
4. Если в области  имеет место неравенство
имеет место неравенство 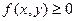 , то
, то 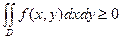 .
.
5. Если в области 
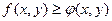 , то
, то 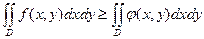 .
.
6. Если функция  непрерывна в замкнутой области
непрерывна в замкнутой области  , площадь которой
, площадь которой 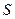 , то
, то 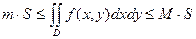 , где
, где 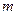 и
и 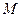 - соответственно наименьшее и наибольшее значения подынтегральной функции в области
- соответственно наименьшее и наибольшее значения подынтегральной функции в области  .
.
7. 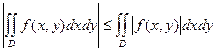 .
.
8. Теорема о среднем
Если функция 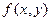 непрерывна в замкнутой области
непрерывна в замкнутой области  , площадь которой
, площадь которой 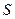 , то в этой области существует такая точка
, то в этой области существует такая точка 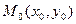 , что
, что 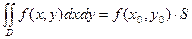 . Величину
. Величину 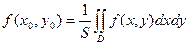 называют средним значением функции
называют средним значением функции 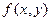 в области
в области  .
.
п. 3 Вычисление двойного интеграла в декартовых координатах.
Вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной интеграл 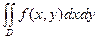 , где функция
, где функция 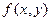 непрерывна в области
непрерывна в области  . Как известно, двойной интеграл выражает объем цилиндрического тела. Найдем этот объем, используя метод параллельных сечений:
. Как известно, двойной интеграл выражает объем цилиндрического тела. Найдем этот объем, используя метод параллельных сечений:
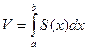 , где
, где 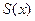 - площадь сечения плоскостью, перпендикулярной оси
- площадь сечения плоскостью, перпендикулярной оси 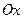 , а
, а 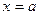 ,
, 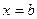 - уравнение плоскостей, ограничивающих данное тело.
- уравнение плоскостей, ограничивающих данное тело.
Пусти область  представляет криволинейную трапецию, ограниченную прямыми
представляет криволинейную трапецию, ограниченную прямыми 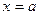 и
и 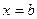 , кривыми
, кривыми 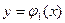 и
и 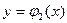 , причем функции
, причем функции 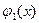 и
и 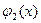 непрерывны и
непрерывны и 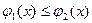 для
для 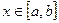 . Область
. Область  правильная в направлении оси
правильная в направлении оси 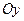 .
.
Постоим сечение цилиндрического тела плоскостью, перпендикулярной оси 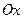 :
: 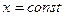 , где
, где 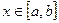 .
.
В сечении получим криволинейную трапецию 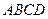 , ограниченную линиями
, ограниченную линиями 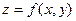 , где
, где 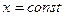 ,
, 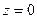 ,
, 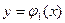 и
и 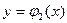 .
.
Площадь данной трапеции находим с помощью определенного интеграла 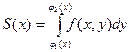 .
.
Согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
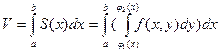 .
.
Объем цилиндрического тела можно вычислить с помощью двойного интеграла 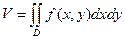 . Следовательно,
. Следовательно, 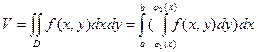 .
.
Данное равенство можно записать в идее:
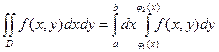 (2)
(2)
Правую часть формулы (2) называют двукратным или повторным интегралом от функции 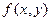 по области
по области  .
.
Интеграл 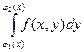 называют внутренним интегралом.
называют внутренним интегралом.
При вычислении двукратного интеграла сначала берем внутренний интеграл, считая 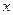 постоянным, а затем внешний интеграл, результат внутреннего интеграла интегрируем по переменной
постоянным, а затем внешний интеграл, результат внутреннего интеграла интегрируем по переменной 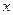 в пределах от
в пределах от 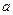 до
до 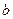 .
.
Если область  ограничена прямыми
ограничена прямыми 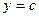 и
и 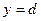 , кривыми
, кривыми 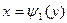 и
и 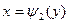 , причем
, причем 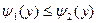 для всех
для всех 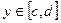 , т.е. область
, т.е. область  - параллельная в направлении оси
- параллельная в направлении оси 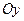 , то
, то
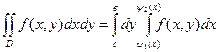 (3)
(3)
В данном случае, при вычислении внутреннего интеграла, считаем 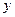 постоянным.
постоянным.
Нужно помнить, что пределы внешнего интеграла всегда постоянны.
Пример 1. Вычислить 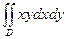 , где область
, где область  ограничена линиями
ограничена линиями 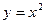 ,
, 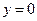 ,
, 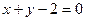 .
.
Решение. Изобразим область интегрирования
Найдем точку пересечения кривых 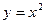 и
и 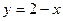 :
:
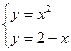 ,
, 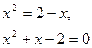 ,
, 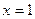 и
и 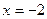
Тогда 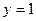 и
и 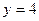 . Нашей области
. Нашей области  принадлежит точка
принадлежит точка 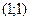 .
.
Для вычисления данного интеграла воспользуемся формулой (3), т.е. спроектируем область  на ось
на ось 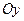 в отрезок
в отрезок 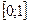 , тогда
, тогда 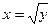 и
и 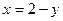 .
.
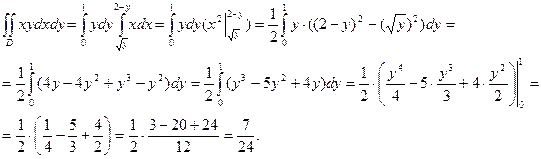
При вычислении данного интеграла по формуле (2) нужно область  разбить прямой
разбить прямой 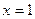 на две область
на две область 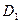 и
и 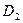 , тогда
, тогда 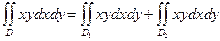 .
.
Область 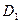 проектируется на ось
проектируется на ось 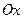 в отрезок
в отрезок 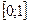 , а область
, а область 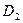 - в отрезок
- в отрезок 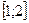 .
.
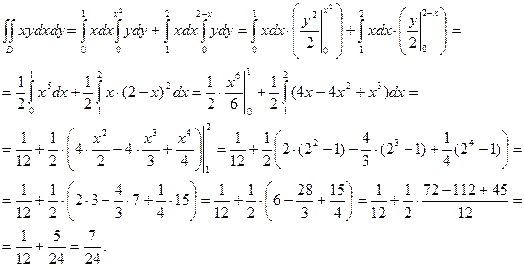
Получили тот же результат.
Если область  является правильной, т.е. всякая прямая параллельная любой оси координат, пересекает границу области не более чем в двух точках, то
является правильной, т.е. всякая прямая параллельная любой оси координат, пересекает границу области не более чем в двух точках, то 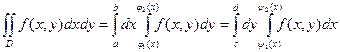 , т.е. двойной интеграл не зависит от порядка интегрирования.
, т.е. двойной интеграл не зависит от порядка интегрирования.
Вопросы для самоконтроля:
1. Что такое интегральная сумма для функции 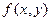 по области
по области  ?
?
2. Что называется двойным интегралом от функции 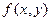 по области
по области  ?
?
3. Геометрический смысл двойного интеграла.
4. Физический смысл двойного интеграла.
5. Какая область  называется правильной в направлении оси
называется правильной в направлении оси 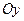 , а какая – в направлении оси
, а какая – в направлении оси 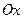 .
.
6. Как вычислить двойной интеграл в декартовых координатах?
7. Как изменить порядок интегрирования в двойном интеграла?
Задание.
1. Вычислить 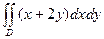 , где
, где  - внутренность треугольника с вершинами
- внутренность треугольника с вершинами 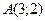 ,
, 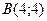 ,
, 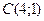 .
.
2. Изменить порядок интегрирования в двойном интеграле 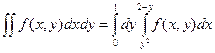 .
.
Литература:
1. Н.С. Пискунов «Дифференциальное и интегральное исчисления» ч.2., гл. XIV, § 1 – 3.
2. П.Е. Данко «Высшая математика в упражнениях и задачах» ч.2., гл. I, § 1.
п 4. Вычисление двойного интеграла в полярных координатах.
Для упрощения вычисления двойного интеграла часто применяют метод подстановки, т.е. вводят новые переменные под знак двойного интеграла.
Пусть 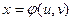 ,
, 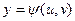 , причем данные функции имеют непрерывные частные производные первого порядка в области
, причем данные функции имеют непрерывные частные производные первого порядка в области 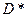 плоскости
плоскости 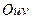 и отличный от нуля определитель
и отличный от нуля определитель
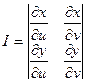 (4)
(4)
Функция 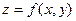 непрерывна в области
непрерывна в области  . Тогда справедлива формула замены переменных в двойном интеграле:
. Тогда справедлива формула замены переменных в двойном интеграле:
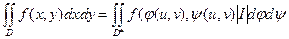 (5)
(5)
Определитель 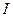 называется определителем Якоби (немецкий математик) или Якобианом.
называется определителем Якоби (немецкий математик) или Якобианом.
Чаще всего при вычислении двойного интеграла переходят к полярным координатам 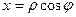 ,
, 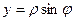 .
.
Вычислим Якобиан перехода к полярным координатам
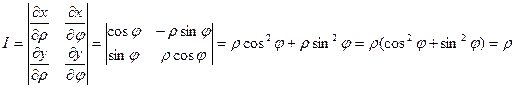 .
.
Тогда
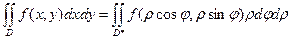 (6),
(6),
Где 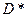 - область интегрирование в полярной системе координат.
- область интегрирование в полярной системе координат.
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведение его к двукратному интегралу.
Пусть область 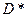 ограничена лучами
ограничена лучами 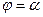 и
и 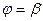 , кривыми
, кривыми 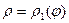 и
и 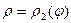 . Если луч , выходящий из полюса пересекает границу области
. Если луч , выходящий из полюса пересекает границу области 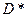 не более чем в двух точках, то область
не более чем в двух точках, то область 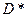 - правильная.
- правильная.
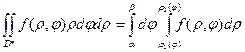 (7).
(7).
При вычислении внутреннего интеграла 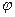 считаем постоянным.
считаем постоянным.
Замечание. Переход к полярным координатам полезен тогда, когда область интегрирования есть круг или его часть и когда подынтегральная функция содержит выражение 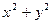 .
.
Пример. Вычислить двойной интеграл 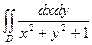 , если область
, если область  ограничена полуокружностью
ограничена полуокружностью 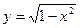 и осью
и осью 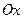 .
.
Решение.
1. Изобразим область 
2. Перейдем к полярным координатам 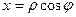 ,
, 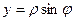 ,
, 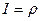 .
.
3. Найдем пределы интегрирования: 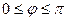 ,
, 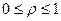 .
.
4. Вычислим интеграл
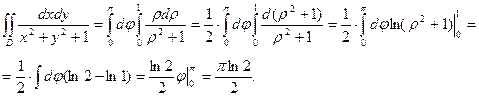
Пример. Вычислить 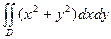 , если область
, если область  ограничена окружностью
ограничена окружностью 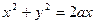 .
.
п 5. Приложение двойного интеграла.
1. Объем тела. Объем цилиндрического тела находится по формуле 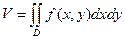 , где
, где 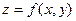 - уравнение поверхности, ограничивающей тело сверху.
- уравнение поверхности, ограничивающей тело сверху.
2. Площадь плоской фигуры. Если подынтегральная функция 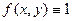 , то получим формулу для вычисления площади плоской области
, то получим формулу для вычисления площади плоской области  :
:
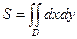 .
.
В полярных координатах
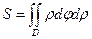 .
.
2’. Вычисление площади поверхности.
1. Если гладкая поверхность задана уравнением 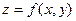 , то площадь поверхности выражается формулой
, то площадь поверхности выражается формулой 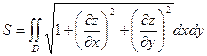 ,
,
где  - проекция данной поверхности на плоскость
- проекция данной поверхности на плоскость 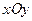 .
.
2. Если гладкая поверхность задана уравнением 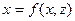 , то
, то 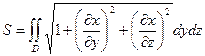 ,
,
где  - проекция данной поверхности на плоскость
- проекция данной поверхности на плоскость 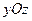 .
.
3. Масса плоской пластинки
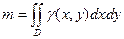 .
.
4. Статистические моменты и координаты центра тяжести плоской пластинки.
Статистические моменты относительно осей координат:
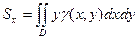 ,
, 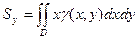 .
.
Координаты центра тяжести
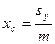 ,
, 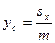 .
.
5. Моменты инерции плоской фигуры.
Моментом инерции математической точки массы 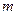 на квадрат распределения
на квадрат распределения 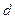 точки до оси:
точки до оси:
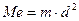 .
.
Моменты инерции плоской фигуры относительно осей 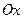 и
и 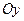 могут быть вычислены по формулам:
могут быть вычислены по формулам:
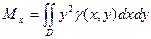 ,
,
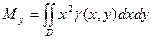 .
.
Момент инерции относительно начала координат:
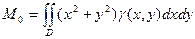 .
.
Пример. Вычислить объем тела, ограниченного поверхностями 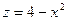 ,
, 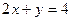 ,
, 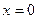 ,
, 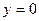 ,
, 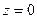 .
.
Решение. Изобразим тело, объем которого нужно вычислить.
Найдем объем тела по формуле 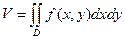 :
:
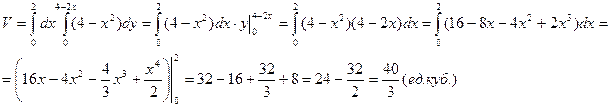
Пример. Найти площадь пластинки, ограниченной линиями 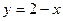 ,
, 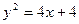 .
.
Решение. Изобразим область  :
:
Найдем точки пересечения кривых:
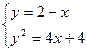 ;
; 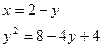
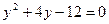 .
.
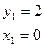
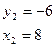
Область  проектируется на ось
проектируется на ось  в отрезок
в отрезок 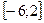 .
.
Площадь вычислим по формуле 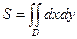 :
:
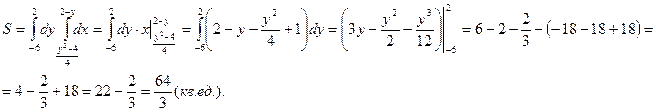 Пример. Вычислить площадь части поверхности
Пример. Вычислить площадь части поверхности 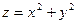 , вырезанной цилиндром
, вырезанной цилиндром 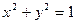 и расположенной в I октанте.
и расположенной в I октанте.
Пример. Найти координаты центра тяжести плоской пластинки, ограниченной линиями 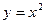 ,
, 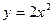 ,
, 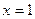 ,
, 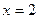 .
.
Вопросы для самоконтроля:
1. Что такое Якобиан перехода и чему он равен в полярных координатах?
2. Выражение двойного интеграла в полярных координатах.
3. Как вычислить объем цилиндрического тела?
4. Как вычислить площадь плоской пластинки?
5. Как найти площадь поверхности?
6. Как вычислить массу пластинки?
7. Как найти координаты центра тяжести пластинки?
8. Как найти моменты инерции плоской фигуры относительно осей 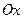 и
и 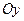 ?
?
Тройной интеграл.
Обобщением определенного интеграла на случай функции трех переменных является тройной интеграл.
Пусть в замкнутой области 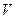 пространства
пространства 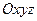 задана непрерывная функция
задана непрерывная функция 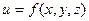 . Разобьем область
. Разобьем область 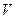 сеткой поверхностей на
сеткой поверхностей на 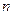 частей
частей 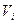 и выберем в каждой из них произвольную точку
и выберем в каждой из них произвольную точку 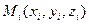 . Составим интегральную сумму
. Составим интегральную сумму 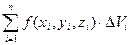 для функции
для функции 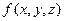 по области
по области 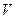 .
.
Если существует предел интегральной суммы при 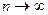 , то этот предел называют тройным интегралом от функции
, то этот предел называют тройным интегралом от функции 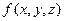 по области
по области 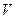 и обозначают
и обозначают 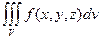 или
или 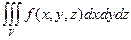 .
.
Т.о. 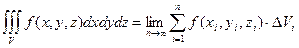 .
.
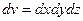 - элемент объема.
- элемент объема.
Теорема. Если функция 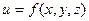 непрерывна в ограниченной области
непрерывна в ограниченной области 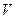 , то предел интегральной суммы существует при
, то предел интегральной суммы существует при 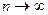 и
и 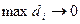 и не зависит ни от способа разбиения области
и не зависит ни от способа разбиения области 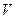 на части, ни от выбора точек
на части, ни от выбора точек 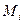 в них.
в них.
Тройной интеграл обладает теми же свойствами, что и двойной интеграл.
1. 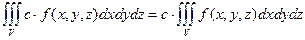 ,
, 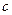 -
- 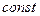 .
.
2. 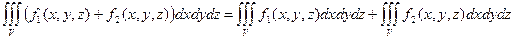 .
.
3. 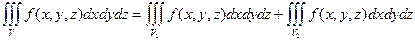 .
. 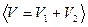 .
.
4. Если в области 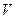
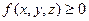 , то
, то 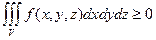 .
.
5. Если во области 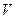
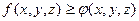 , то и
, то и 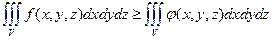 .
.
6. Если 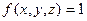 , то
, то 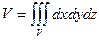 .
.
7. 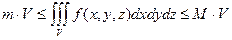 , где
, где 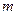 и
и 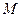 - соответственно наименьшее и наибольшее значения функции
- соответственно наименьшее и наибольшее значения функции 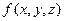 в области
в области 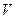 .
.
8. Теорема о среднем: если функция 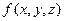 непрерывна в замкнутой области
непрерывна в замкнутой области 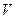 , то в этой области существует такая точка
, то в этой области существует такая точка 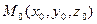 , что
, что 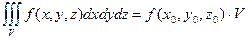 , где
, где 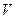 - объем тела.
- объем тела.
п 6. Вычисление тройного интеграла в декартовых координатах.
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.
Пусть областью интегрирования является тело, ограниченное снизу поверхностью 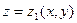 , сверху - поверхностью
, сверху - поверхностью 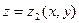 , причем
, причем 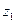 ,
, 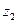 - непрерывные функции в замкнутой области
- непрерывные функции в замкнутой области  и
и 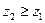 .
.
 - проекция тела на плоскость
- проекция тела на плоскость 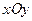 .
.
Область 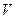 называется правильной в направлении оси
называется правильной в направлении оси 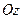 , если любая прямая, параллельная оси
, если любая прямая, параллельная оси 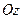 , пересекает границу области не более чем в двух точках.
, пересекает границу области не более чем в двух точках.
Тогда, если 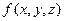 непрерывна в области
непрерывна в области 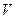 , то имеет место формула
, то имеет место формула
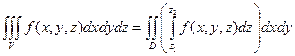 .
.
При этом, сначала вычисляется интеграл по переменной 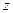 при постоянных
при постоянных 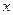 и
и 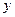 , а затем двойной интеграл. Нижней границей является аппликата точки
, а затем двойной интеграл. Нижней границей является аппликата точки 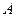 входа в область
входа в область 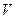 , верхней границей аппликата точки
, верхней границей аппликата точки 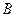 - точка выхода прямой из области
- точка выхода прямой из области 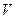 .
.
Результатом вычисления есть функция двух переменных 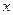 и
и 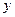 .
.
Если область  ограничена линиями
ограничена линиями 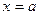 ,
, 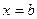 ,
, 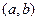 ,
, 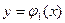 и
и 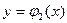 , где
, где 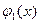 и
и 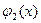 - непрерывные на отрезке
- непрерывные на отрезке 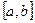 функции, причем
функции, причем 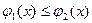 , то переходя от двойного интеграла по области
, то переходя от двойного интеграла по области  к повторному, получим формулу:
к повторному, получим формулу:
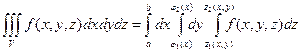
Порядок интегрирования может быть изменен.
Пример. Вычислить 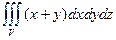 , где
, где 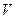 - ограничена плоскостями
- ограничена плоскостями 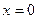 ,
, 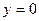 ,
, 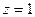 ,
, 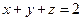 .
.
Решение.
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах.
При вычислении тройного интеграла, как и двойного, часто применяются метод подстановки: 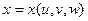 ,
, 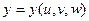 ,
, 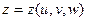 . Если данные функции имеют непрерывные частные производные и отличный от нуля определитель
. Если данные функции имеют непрерывные частные производные и отличный от нуля определитель 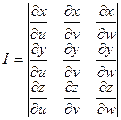 , то справедлива формула замены переменных в тройном интеграле:
, то справедлива формула замены переменных в тройном интеграле:
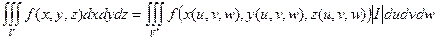 .
.
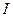 - якобиан преобразования.
- якобиан преобразования.
1. Тройной интеграл в цилиндрических координатах.
Положение точки 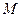 в пространстве
в пространстве 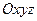 можно определить заданием трех чисел
можно определить заданием трех чисел 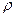 ,
, 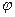 ,
, 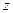 , где
, где 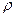 - длина радиус-вектора проекции точки
- длина радиус-вектора проекции точки 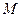 на плоскость
на плоскость 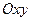 ,
, 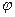 - угол, образованный этим радиусом-вектором с осью
- угол, образованный этим радиусом-вектором с осью 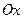 ,
, 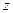 - аппликата точки
- аппликата точки 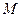 .
.
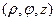 - цилиндрические координаты точки
- цилиндрические координаты точки 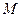 .
.
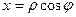
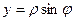
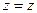 , причем
, причем 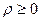 ,
, 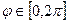 ,
, 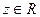 .
.
Якобиан преобразования:
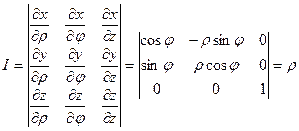 .
.
Формула замены переменных примет вид:
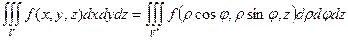 .
.
Замечание. К цилиндрическим координатам переходят в том случае, когда область интегрирования образована цилиндрической поверхностью.
Пример. Вычислить 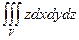 , где
, где 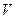 - область, ограниченная верхней частью конуса
- область, ограниченная верхней частью конуса 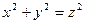 и плоскостью
и плоскостью 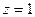 .
.
Решение.
2. Тройной интеграл в сферических координатах.
