Уравнение касательной к графику функции

Чтобы закрепить предыдущий параграф, рассмотрим задачу нахождения касательной к графику функции в данной точке. Это задание встречалось нам в школе, и оно же встречается в курсе высшей математики.

Рассмотрим «демонстрационный» простейший пример.

Составить уравнение касательной к графику функции 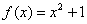в точке с абсциссой 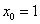. Сразу приведём готовое графическое решение задачи (на практике этого делать в большинстве случаев не надо):

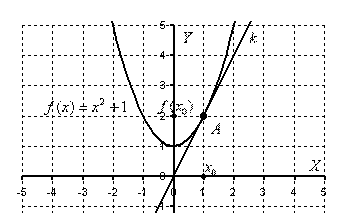
Строгое определение касательной дается с помощью определения самой производной функции, и с этим пока повременим. Наверняка практически всем интуитивно понятно, что такое касательная.

Если объяснять «на пальцах», то касательная к графику функции – это прямая, которая касается графика функции в единственной точке. При этом все близлежащие точки прямой расположены максимально близко к графику функции.

Применительно к нашему случаю: при 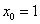касательная с угловым коэффициентом k (стандартное обозначение) касается графика функции в единственной точке .

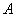И наша задача состоит в том, чтобы найти уравнение прямой k.

Как составить уравнение касательной в точке с абсциссой ?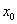

Общая формула знакома нам еще со школы:

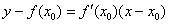
Значение 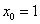нам уже дано в условии.

Теперь нужно вычислить, чему равна сама функция в точке :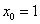

.

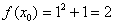На следующем этапе находим производную:

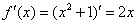
Находим производную в точке (задание, которое мы недавно рассмотрели):

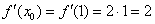
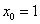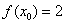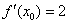Подставляем значения , и в формулу :

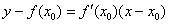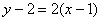
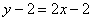
Таким образом, уравнение касательной:

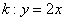
Это «школьный» вид уравнения прямой с угловым коэффициентом. В высшей математике уравнение прямой принято записывать в так называемой общей форме 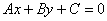, поэтому перепишем найденное уравнение касательной в соответствии с традицией:

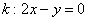
Очевидно, что точка 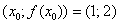должна удовлетворять данному уравнению:

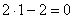
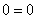– верное равенство.

Следует отметить, что такая проверка является лишь частичной. Если мы неправильно вычислили производную в точке 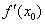, то выполненная подстановка нам ничем не поможет.

Рассмотрим еще два примера.

Пример 5

Составить уравнение касательной к графику функции 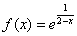в точке с абсциссой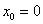

Уравнение касательной составим по формуле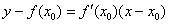

1) Вычислим значение функции в точке :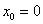

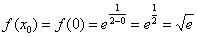
2) Найдем производную. Дважды используем правило дифференцирования сложной функции:

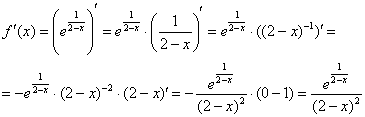
3) Вычислим значение производной в точке :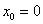

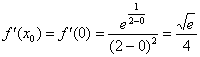
4) Подставим значения 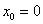, 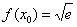и 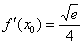в формулу :

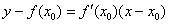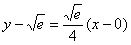
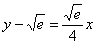
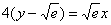
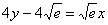
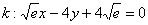
Готово.

Выполним частичную проверку:

Подставим точку 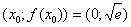в найденное уравнение:

;

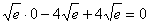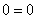; – верное равенство.

Пример 6

Составить уравнение касательной к графику функции 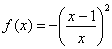в точке с абсциссой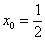

Полное решение и образец оформления в конце урока.

В задаче на нахождение уравнения касательной очень важно ВНИМАТЕЛЬНО и аккуратно выполнить вычисления, привести уравнение прямой к общему виду.