Элементы математической статистики

Выборочной совокупностьюили просто выборкой называют совокупность объектов, случайно отобранных из генеральной совокупности.

Число объектов в совокупности называется ее объемом.

Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот.

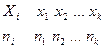
Эмпирической функцией распределения (ЭФР) называется функция 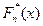, определяющая для каждого значения х относительную частоту события (X<x),

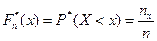
где n_x – число наблюдений, при которых наблюдалось значение признака, меньше х.

Функцию распределения 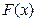называют теоретической функцией распределения (ТФР).

ТФР определяет вероятность события (X<x), ЭФР – частоту этого события. ЭФР является оценкой ТФР.

Полигоном частот называют ломаную, отрезки которой соединяют точки (x₁;n₁), (x₂; n₂),…(x_k; n_k) На оси ОХ откладываются варианты, на оси ОУ – частоты.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению n_i/h - эта величина называется плотностью частоты

Выборочной средней 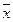называется среднее арифметическое всех значений выборки.

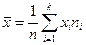
Выборочная дисперсия D есть среднее арифметическое квадратов отклонений значений выборки от выборочной средней

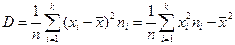
Выборочное среднее квадратическое отклонение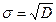

Исправленная выборочная дисперсия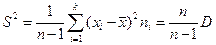

Исправленное выборочное среднее квадратическое отклонение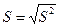

Модойвариационного ряда называется варианта, имеющая наибольшую частоту.

Медианой вариационного ряда называется варианта, приходящаяся на середину ряда.

Доверительный интервал для математического ожидания при известной дисперсии для нормального распределения генеральной совокупности.

Пусть Х имеет нормальное распределение с параметрами а, σ, причем σ известна и γ задана. Тогда доверительный интервал для неизвестного параметра а:

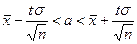
где n – объем выборки, 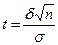- определяется по таблице приложения 2 из уравнения Φ(t)=γ/2.

Доверительный интервал для математического ожидания при неизвестной дисперсии для нормального распределения генеральной совокупности.

Пусть Х имеет нормальное распределение с параметрами а, σ, причем σ неизвестна и γ задана. Тогда доверительный интервал для неизвестного параметра а:

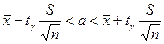
где S – исправленное среднее квадратическое отклонение, 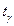- квантиль уровня 1-γ и числа степеней свободы n-1 (приложение 3)

Доверительный интервал для среднего квадратического отклонения нормального распределения при неизвестном математическом ожидании.

Пусть Х имеет нормальное распределение с параметрами а, σ, причем а и σ неизвестна и γ задана. Тогда доверительный интервал для неизвестного параметра σ:

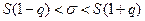
где S – исправленное среднее квадратическое отклонение, q - определяется по таблице приложения 4.