МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ № 2
1. Задание 1
по теме «Частные производные функции
нескольких переменных»
Краткие теоретические сведения
Понятие функции нескольких переменных
Пусть имеется п переменных величин и каждому набору их значений (х1, х2, …, хп) из некоторого множества Х соответствует одно вполне определенное значение переменной величины z. Тогда говорят, что задана функция нескольких переменных z = f(х1, х2, …, хп).
Пример. Формула z = х1 · х2 · х3 задает объем прямоугольного параллелепипеда как функцию трех его измерений х1, х2, х3.
Пример. В экономической теории часто используется так называемая функция полезности, ставящая в соответствие каждому набору (х1, х2, …, хп), который интерпретировался выше как набор товаров в соответствующих единицах измерения, функцию z = f(х1, х2, …, хп), выражающую полезность от этих приобретенных п товаров. Чаще всего используются следующие виды функции f :
1. Логарифмическая функция
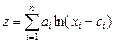 ,
,
где 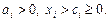
2. Функция постоянной эластичности
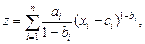
где 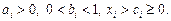
Функция двух переменных и ее график
Будем рассматривать в дальнейшем случай n = 2 и функцию
z = f(x, y) двух переменных x, y.
Для ее изучения используется развитый математический аппарат для функции одной переменной. Любой функции z = f(x, y) можно поставить в соответствие пару функций одной переменной, т. е. при фиксированном значении x = x0 — функцию z = f(x0, y) и при фиксированном значении y = y0 — функцию z = f(x, y0).
Графиком функции z = f(x, y) называется множество точек пространства R3, в которых координата z связана с координатами х и у уравнением z = f(x, y).
В общем случае, график функции z = f(x, y) — некоторая поверхность в R3 (рис. 17).
Рис. 17
Частные производные первого порядка
Частной производной функции z = f(x, y) по независимой переменной x называется конечный предел
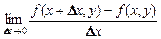 =
= 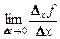 =
= 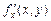 ,
,
а частной производной этой функции по независимой переменной у называется конечный предел
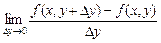 =
= 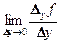 =
= 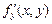 .
.
Обозначается частная производная так: 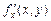 ,
, 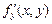 , или
, или 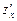 ,
, 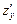 , или
, или 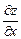 ,
, 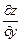 .
.
Для частных производных функции нескольких переменных справедливы обычные правила и формулы дифференцирования.
Полный дифференциал
Полным приращением функции z = f(x,y) в точке М(х,у)называется разность 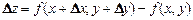 , где
, где 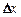 ,
, 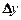 — произвольные приращения аргументов.
— произвольные приращения аргументов.
Функция z = f(x,y) называется дифференцируемой в точке (x,y), если ее полное приращение может быть представлено в виде
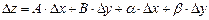 ,
,
где А и В, не зависящие от 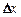 и
и 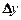 , — постоянные;
, — постоянные; 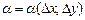 ,
, 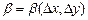 — бесконечно малые при
— бесконечно малые при 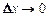 ,
, 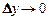 функции, равные нулю при
функции, равные нулю при 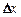 =
= 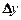 = 0.
= 0.
Полным дифференциалом функции z = f(x, y) называется главная часть полного приращения 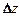 , линейная относительно приращений аргументов
, линейная относительно приращений аргументов 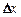 ,
, 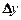 , т. е.
, т. е. 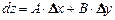 .
.
Для независимых переменных х, у полагают, что 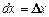 ,
, 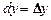 .
.
Поэтому полный дифференциал функции z = f(x, y) вычисляется по формуле
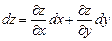 .
.
Пример. Для функции z = x2y получим:
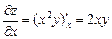 ,
, 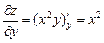 , dz = 2xy dx + x2dy.
, dz = 2xy dx + x2dy.
Вопросы для самопроверки
1. Что вы понимаете под функцией нескольких переменных?
2. Какие вы знаете примеры функций нескольких переменных?
3. Что называется частной производной функции двух переменных?
4. Как вычислить полное приращение функции z = f(x, y) в произвольной точке?
5. Какая функция называется дифференцируемой в точке (x, y)?
6. Что называется полным дифференциалом функции z = f(x, y)?
7. По какой формуле вычисляется полный дифференциал функции двух переменных?
Типовая задача 1
Показать, что функция и = у · ln(x2 – y2) удовлетворяет соотношению 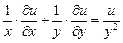 .
.
Решение. Находим частные производные:
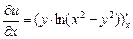 =
= 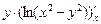 =
= 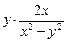 =
= 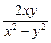 ,
,
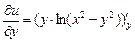 =
= 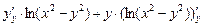 = ln(x2 –
= ln(x2 –
– y2) + 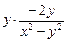 = ln(x2 – y2) –
= ln(x2 – y2) – 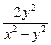 .
.
Подставляем полученные значения в соотношение:
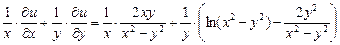 =
= 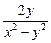 +
+
+ 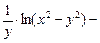
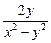 =
= 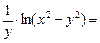
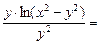
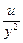 , что и требовалось показать.
, что и требовалось показать.
2. Задания 2 и 3
по теме «Неопределенный интеграл,
определенный интеграл и его применение
для вычисления площади фигуры»
