Тема 8.2. Геометрия Лобачевского

План лекции:

1. Аксиомы Лобачевского

2. Д. Гильберт

После III в. до н.э. геометрия развивалась медленно - тре­бовались новые идеи и методы, необходимо было развитие понятия числа и алгебры. Первые шаги в этом направлении были сделаны в Греции (работы Диофанта, III в.), а затем в Индии, где были открыты десятичная система счисления, от­рицательные и иррациональные числа.

В IX в. благодаря работам Мухаммеда аль-Хорезми даль­нейшее развитие получила алгебра. Позже таджикский поэт и ученый Омар Хайям (конец XI - начало XII в.) дал определение числа как отношения любых величин. Через 600 лет это же оп­ределение было дано Ньютоном во «Всеобщей арифметике». В геометрии новые идеи и методы появились в XVII в. Они были обусловлены развитием алгебры и созданием математиче­ского анализа. Принадлежали эти идеи французскому филосо­фу и математику Рене Декарту. В своем сочинении «Геометрия» он впервые представил метод координат на плоскости, устано­вив тем самым взаимосвязь геометрии с алгеброй.

Важным направлением в развитии геометрии был поиск логически безупречного построения геометрии. Дело в том, что аксиоматически построенная теория должна удовлетво­рять определенным требованиям математической строгости. Они не абсолютны и в разные периоды истории были различ­ными. Эти требования заставили обратить особое внимание на пятый постулат геометрии Евклида - его трудно было принять очевидным, как остальные аксиомы постулаты. Поэтому возникло стремление вывести его из остальных по­стулатов и аксиом. Однако попытки, которые длились более двух тысяч лет, были безуспешными, хотя и сыграли положи­тельную роль в развитии геометрии, так как были сформули­рованы и доказаны теоремы, раскрывающие новые свойства геометрических фигур.

Переворот в геометрии произошел в начале XIX в., когда несколько ученых пришли к мысли о существовании геомет­рии, отличной от евклидовой. Первым, кто построил эту гео­метрию, был Н. И. Лобачевский, профессор Казанского уни­верситета. Его рассуждения сводились к следующему.

Рассмотрим в плоскости прямую а и проведем из точки А перпендикуляр АС к прямой а и луч АВ, перпендикулярный АС (рис. 132). Возьмем некоторую прямую AM, пересекаю­щую прямую а в точке М. При неограниченном удалении точки М по прямой а прямая AM будет приближаться к неко­торому предельному положению. Логически могут предста­виться две возможности:

а) луч AM совпадает с лучом АВ;

б) луч AM составит с лучом АВ некоторый острый угол.

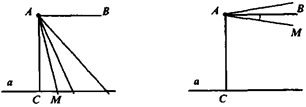
Случай а) соответствует аксиоме параллельности: АВ- единственная прямая, проходящая через А и не пересекающая а.

Допуская, что имеет место случай б), Лобачевский начал выводить различные следствия из этого допущения, надеясь, что рано или поздно придет к противоречию, чем и завершится доказательство. Однако, доказав несколько десятков теорем, он так и не обнаружил логических противоречий. И тогда Лоба­чевский высказал мысль: если заменить пятый постулат его отрицанием (т.е. принять, что через точку вне прямой можно провести более одной прямой, ей параллельной) и сохранить все остальные аксиомы евклидовой геометрии, то получим новую геометрию, которую он назвал «воображаемой», а позд­нее она была названа его именем - геометрией Лобачевского.

Все теоремы, доказываемые в евклидовой геометрии без использования пятого постулата, сохраняются и в геометрии Лобачевского.

Например, вертикальные углы равны; углы при основании равнобедренного треугольника равны;

из дан­ной точки можно опустить на данную прямую только один перпендикуляр.

Теоремы же, при доказательстве которых применяется пятый постулат, в геометрии Лобачевского ви­доизменяются, например сумма величин внутренних углов любого треугольника меньше 180°, не существует подобных треугольников: если углы двух треугольников соответственно равны, то эти треугольники равны. Так как в геометрии Ло­бачевского сумма внутренних углов четырехугольника мень­ше 360°, то в ней не существует прямоугольников. Позже было доказано, что аксиоматика, предложенная им, независима и непротиворечива.

Открытие, сделанное Н. И. Лобачевским, сыграло огром­ную роль в развитии математики и физики. В его работах была не только полностью решена проблема независимости аксиомы параллельности от других аксиом евклидовой геометрии, но и было показано, что аксиомы могут подвергаться изменению, что привлекло внимание ученых к вопросам аксиоматики гео­метрии. Кроме того, было установлено, что геометрия Лоба­чевского точно описывает взаимосвязь пространства и време­ни, открытую А. Эйнштейном в теории относительности.

После открытия Н. И. Лобачевского стало ясно, что пятый постулат (аксиома параллельности) не может быть исключен из списка аксиом и постулатов, сформулированных Евклидом. Общая тенденция к повышению строгости построения матема­тических теорий во второй половине XIX в. сказалась и в гео­метрии. Она выразилась в стремлении дополнить систему акси­ом евклидовой геометрии, включив в нее все предложения, ко­торые неявно использовались при доказательстве теорем.

Итог всем исследованиям в этой области подвел крупней­ший немецкий математик Д. Гильберт. Произошло это в конце XIX столетия. В своей книге «Основания геометрии» он дает полный список аксиом евклидовой геометрии и доказывает непротиворечивость этой аксиоматики. Сформулированные им аксиомы относятся к точкам, прямым, плоскостям и отношени­ям между ними, которые выражаются словами «принадлежит», «лежать между», «конгруэнтен». Что такое точка, прямая и плоскость и каков конкретный смысл указанных отношений, Гильберт не уточняет. Все, что предполагается известным о них, выражено в аксиомах. Они разбиты на пять групп.

Первая группа - аксиомы принадлежности. В них устанав­ливаются отношения между точками, прямыми и плоскостями.