Временные и частотные характеристики
Временные характеристики h(t) и g(t) называют переходной характеристикой и импульсной переходной характеристикой соответственно
Переходная характеристика h(t) – определяет реакцию звена на входной сигнал 1(t):
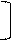t -1 W(p)
h(t)= ò g(t) dt = L p , (2.5)
где L -1 - обратное преобразование Лапласа.
Другой важной характеристикой динамического звена является частотная характеристика. При подаче на вход звена гармонического воздействия
х вх= Авх× sin (wt) (2.6)
где А- амплитуда воздействия, а w - его угловая частота, на выходе звена в установившемся режиме будет получена также гармоническая функция
x вых= Авых·sin(wt+j), (2.7)
отличающаяся от входного воздействия и по амплитуде и по фазе. Представим входную и выходную гармонические функции в экспоненциальном виде:
х вх= Авх× ejwt (2.8)
x вых= Авых· ejwt+j,
а частотную передаточную функцию получим, подставляя в
W(p) выражение р=jw, j=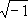 
.
Выделим действительную и мнимую части частотной передаточной функции
W(jw)=P(w)+jQ(w), (2.9)
и запишем в экспоненциальном виде
W(jw)=A(w)·еjw, (2.10)
где A(w) – амплитуда (модуль частотной передаточной функции):
A(w) =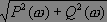 
(2.11)
j(w)– аргумент (фаза) частотной передаточной функции:
j(w)=arg(W(jw))=arctg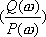 
. (2.12)
Для наглядного представления частотных свойств динамических звеньев используют частотные характеристики.
1. Амплитудно-частотная характеристика (АЧХ) опреде-
ляет зависимость амплитуды выходного сигнала от частоты колебаний при постоянной амплитуде входного сигнала (рис. 2.1).
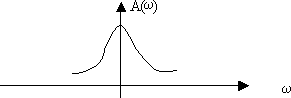
Рис. 2.1
1. Фазовая частотная характеристика (ФЧХ) показывает фазовые сдвиги, вносимые звеном на разных частотах (рис. 2.2).
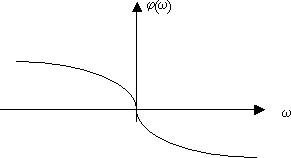
Рис. 2.2
3. Амплитудно-фазовая частотная характеристика
(АФЧХ, или годограф) объединяет АЧХ и ФЧХ при использовании их в качестве полярных координат (рис. 2.3).
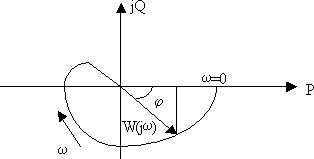
Рис. 2.3
4. Иногда целесообразно использовать вещественную и мнимую частотные характеристики P(w) и Q(w) из формулы (2.9).
Связь между перечисленными частотными характеристиками определяется формулами (2.11) и (2.12), а также соотношениями
P(w)=A(w)cos (jw) (2.13)
Q(w)=A(w)sin (jw) 
5.Наиболее удобными в использовании являются логарифмические частотные характеристики ЛАХ и ЛФХ.
Прологарифмируем выражение частотной передаточной функции (2.9).
ln(W(jw))=ln(A(w)еjw)=lnA(w)+jj(w) (2.14)
Величину lnA(w) называют логарифмической амплитудной частотной характеристикой (ЛАХ), а j(w) - логарифмической фазовой частотной характеристикой (ЛФХ).
Для построения ЛАХ используют формулу:
L(w)=20lgA(w). (2.15)
Величина L(w) выражается в децибелах. Децибел – это 0,1 бела, а бел – логарифмическая единица, которая соответствует десятикратному увеличению мощности (1 бел – в 10 раз, 2 бела – в 100 раз, 3 бела - в1000 раз).
ЛАХ строится в логарифмическом масштабе частот в стандартной логарифмической сетке (рис. 2.5).
По оси абсцисс откладывается угловая частота w в логарифмическом масштабе, при этом отрезки оси, соответствующие изменению частоты в одинаковое число раз оказываются равными.
Интервал частот , отличающихся друг от друга в 10 друг от друга в 10 раз, называют декадой и обычно принимают за единицу логарифмического масштаба частот масштаба частот.
Ось ординат может пересекать ось абсцисс в произвольном месте. Обычно располагают вертикальную ось так, чтобы с права от нее находился диапазон частот, существенных для данного устройства.
Главное достоинство логарифмического метода – это возможность построения частотных характеристик непосредственно по виду передаточной функции.
Кроме того, использование логарифмического масштаба позволяет охватить большой диапазон частот.
ЛАХ строится в координатной сетке, изображённой на рис. 2.4.
.
Рис. 2.4
ЛФХ строится в координатной сетке, аналогичной изображённой на рис. 2.4, а на оси ординат (j(w),град) принято выделять значения 0, ±45, ± 90, ±135, ± 180, ±225 град.
Рекомендуется совмещать две координатные сетки так, чтобы ось L(w)=0 ЛАХ совпадала с осью j(w)=-180° ЛФХ.
Основные типы ЛДЗи их основные характеристики приведены в [1]
на с.27-39.