Прямые оценки качества регулирования

Прямые оценки качества определяются по переходной характе­ристике, т.е. реакции системы на единичный скачок при нулевых начальных условиях (рисунок 15.2).

Время регулирования t_рег измеряется от начала переходного процесса до момента, после которого характеристика не отклоняется от установившегося значения более, чем на величину допустимой ошибки ∆ (обычно 5 %, реже 2 % от установившегося значения). Следует указывать, при какой зоне Δ получено время регулирования.

Перерегулирование σ – величина максимального относительного заброса переходной характеристики от начальной величины за линию установившегося значения (в относительных единицах или %)

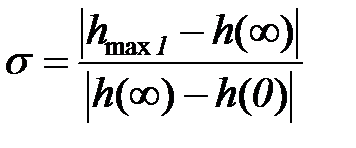или .

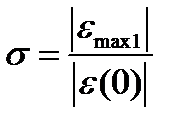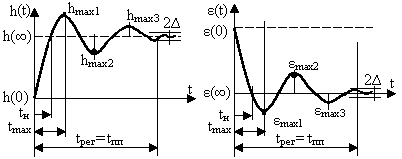
а) – выходная величина y(t) б) – ошибка регулирования ε(t)

или h(t) или отклонение δ(t)

Рисунок 15.2

Если начальное и конечное значения характеристики равны нулю или одинаковы (и приняты условно за 0), возможны два способа оценки. При наличии разнополярных значений перерегулирование равно отношению величины второго экстремума к величине первого (рисунок 15.3, а), а если колебание одно (рисунок 15.3, б), то перерегулирование равно отношению величины максимального отклонения к величине входного воздействия (обычно это единица). Зону Δ для оценки времени регулирования в первом случае определяют от значения первого максимума, во втором случае – от величины входного воздействия.

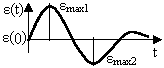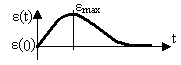а б

Рисунок 15.3

Время нарастания t_н определяется: для процессов с перерегулированием как время от начала процесса до момента пересечения кривой линии установившегося значения; для любых процессов как время между моментами достижения заданных уровней установившегося значения (например, 10 и 90 %). Поэтому при оценке времени нарастания следует указывать, каким способом оно получено.

Время достижения первого максимума t_max (подразумевается, что первый максимум кривой является и наибольшим из всех).

Коэффициент колебательностиN – число забросов переходной характеристики через линию установившегося значения за время ре­гулирования, рекомендуется не более одного-двух забросов.

Степень затухания (демпфирования) – величина относительного уменьшения ψ = (h_max1 - h_max3)/(h_max1 –h(∞))амплитуды максимальных забросов выходной величины за один период Т_к, удовлетворительной считают систему с ψ = 0,75...0,95.

Установившаяся ошибка ε(∞) равна разнице между предписанным и действительным значениями выходной величины после окончания переходного процесса.

Пример 1. Оценить время регулирования и перерегулирование для системы с передаточной функцией k/(s + 2).

Поскольку полюс α = -2 действительный, без мнимой части, колебаний не будет и перерегулирование σ = 0. Переходный процесс описывается зависимостью k(1 - e^αt) и заканчивается при достижении величины 0,95k, т.е. когда выполняется условие e^αt = Δ = 0,05. Отсюда t_рег =ln(Δ)/α = ln(0,05)/(-2) = 1,498 с.

Пример 2. Определить величину перерегулирования и времени регулирования (рисунок 15.4

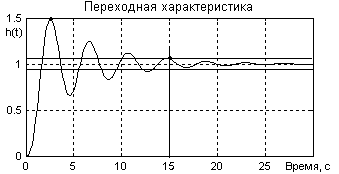
Рисунок 15.4

Перерегулирование σ = (1,5 – 1,0)/1,0 = 0,5 или 50 %. Для определения времени регулирования проводим параллельно линии установившегося значения две прямые на уровне h_уст ±Δ = 1±0,05×1 = 1±0,05. По точке последнего вхождения кривой в зону 2Δ получаем t_рег = 15 с.

15.2 Корневые критерии качества переходных процессов

Эта группа критериев основана на оценке качества переходных процессов по значениям полюсов и нулей передаточной функции системы между интересующими нас входами и выходами системы.

Как известна, переходная характеристика системы может быть определена следующим образом –

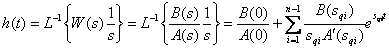(15.1)

где 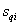– корни характеристического уравнения системы

.

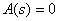Очевидно, что на характер переходного процесса оказывает влияние и числитель 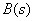и знаменатель 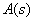передаточной функции. Но, в большинстве случаев, при анализе систем по реакции на управляющее воздействие, 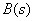не имеет корней, то есть передаточная функция не имеет нулей. Тогда характер переходного процесса можно оценить только по полюсам передаточной функции, подвергая тем самым анализу корни характеристического уравнения системы –

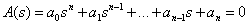(15.2)

В случае приближенной оценки качества по корням характеристического уравнения на комплексной плоскости выделяют область расположения корней, границы которой задаются по требованиям к качеству процессов, как это показано на рис. 15.5.

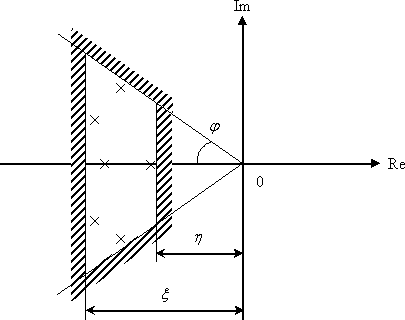
Рис. 15.5

Границы области, показанной на рис. 15.5, задаются следующими параметрами:

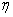· – критерий длительности переходного процесса,

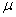· – колебательность переходного процесса, определяется по ,

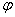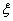· – максимальное удаление корня от мнимой оси.

Рассмотрим эти параметры.

Критерий длительности 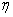определяется как расстояние от мнимой оси до ближайшего действительного корня или ближайшей пары комплексно сопряженных корней.

Выясним, действительно ли этот параметр характеризует длительность переходного процесса? Возможны два случая расположения корней на границе области.

1. Пусть ближайшим к мнимой оси, то есть лежащий на границе области, будет действительный корень –

,

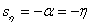тогда соответствующая ему компонента переходного процесса, в соответствии с (15.1) будет иметь вид –

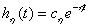	(15.3)

где 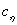- коэффициент разложения (15.1).

2. Если ближайшей к мнимой оси будет комплексно-сопряженная пара корней –

,

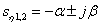тогда соответствующая им компонента переходного процесса, в соответствии с (15.1) будет иметь вид –

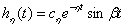(15.4)

где 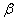- частота колебаний.

Из (15.2) и (15.4) мы видим, что время затухание компоненты 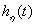определяет сомножитель –

,

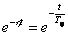где 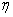– величина минимального действительного корня или минимальной действительной части корней, 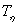– соответствующая 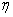, наибольшая постоянная времени. Таким образом, можно считать, что переходный процесс системы завершится не раньше, чем затухнет компонента 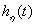. Следовательно, 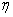определяет длительность переходного процесса, будучи величиной, обратно пропорциональной времени регулирования. Зная 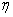, мы можем оценить время регулирования или переходного процесса по следующему соотношению –

,

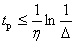где – половина ширины области, при попадании в которую переходной процесс считается завершенным. Если 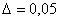, а крайний корень действительный, то имеем –

.

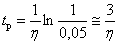Критерий колебательности 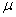определяется по углу 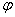следующим образом –

.

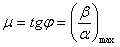где 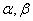– соответственно действительная и мнимая части комплексно сопряженной пары корней расположенных на границе области (см. рис. 15.5). При увеличении 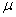возрастает колебательность системы.

Дальнюю от мнимой оси границу области 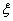, определяют корни, оказывающие предельно малое влияние на переходный процесс.

При прочих равных условиях от системы требую увеличения 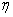и снижения .

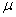В качестве примера влияния расположения корней на характер переходных процессов покажем графики, представленные на рис. 15.6 и 15.7.

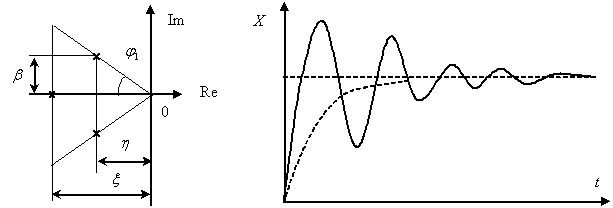
Рис. 15.6

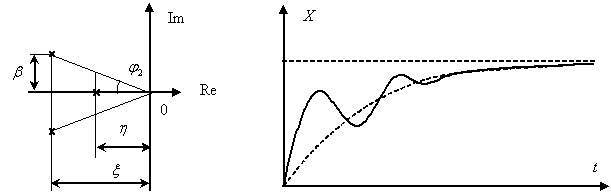
Рис. 15.7

Если передаточная функция системы имеет нули, то оценка качества системы только по полюсам может дать существенную погрешность.

Доминирующими называются левые полюса системы, ближайшие к мнимой оси. Степень устойчивости α_min (или η) равна модулю их действительной части (рисунок 15.8). Для оценки времени регулирования t_регнаходят сначала степень устойчивости системы, откуда при ошибке ∆=5 % t_рег ≈ 3/|α_min|. При заданной зоне ошибки 2 % вместо коэффициента 3 берут приблизительно 4.

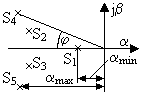
Рисунок 15.8

Найдя степень колебательности системы 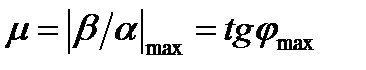, определяют значение перерегулирования 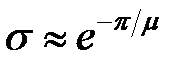. Для расчета μ выбирают комплексный корень (полюс), у которого отношение мнимой части к действительной максимально. При единственной паре комплексных корней необходимость выбора отпадает. При нескольких парах комплексных корней максимальное значение μ у того корня, который первым встречается лучу, проведенному из начала координат по положительной мнимой полуоси и поворачиваемому против часовой стрелки.

Показатели качества определяют только для устойчивых систем. Если система имеет нуль, равный полюсу, то они взаимно компенсируются и данная составляющая не учитывается (выпадает из переходного процесса).

Пример 1. Оценить показатели качества регулирования системы, имеющей нуль -0,125, полюса -1,5 ± 6j; -0,125 и коэффициент передачи 1,2.

Коэффициент передачи на относительные показатели не влияет. Нуль -0,125, равный полюсу, взаимно с ним компенсируется. Следовательно, доминирующими являются комплексно-сопряженные полюса -1,5 ± 6j, откуда t_рег ≈ 3/|α_min| = 3/1,5 = 2 с, степень колебательности системы 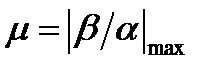= 6/1,5 = 4 и перерегулирование 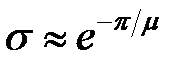= 0,456 или 45,6 %.

Пример 2. Оценить перерегулирование и время регулирования системы 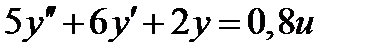с законом управления u = 2(r – y).

Подставляя значение u в соответствии с законом регулирования, получим дифференциальное уравнение 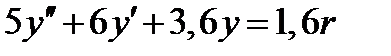. Нули отсутствуют, из характеристического уравнения 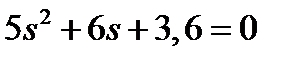находим полюса -0,6 ± j0,6. Отсюда t_рег ≈ 3/|α_min| = 3/0,6 = 5 c, а перерегулирование 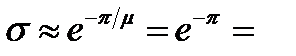0,043 или 4,3 %.