Решение задач и моделирование
МОДЕЛИРОВАНИЕ ПРИ РЕШЕНИИ ИНЖЕНЕРНЫХ ЗАДАЧ
Решение задач и моделирование
Любой материальный объект характеризуется бесчисленным множеством свойств, признаков и характеристик, но наши знания о материальном объекте конечны и относительны на любом этапе развития.
В процессе познания у человека (субъекта) формируется мысленный образ объекта, который обладает присущими этому объекту свойствами (цвет, запах, размеры, вес, изменчивость во времени и др.). Такой мысленный образ есть мысленная (идеальная) модель объекта (рис. 1.1).
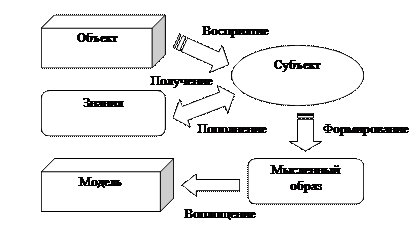
Рис. 1.1. Схема формирования модели
Познавательный процесс человека носит целенаправленный характер, а именно: во всех случаях субъект решает некоторую задачу для достижения своих целей. Задача выделяет из бесконечного множества свойств объекта конечную совокупность и дает возможность перейти к обозримому по своим масштабам «заместителю» объекта – модели. Задача – это фильтр, позволяющий отсеять из всей информации об объекте несущественную.
Таким образом, задача определяет характер формируемой модели.
Рассмотрим несколько примеров.
Пример 1. Сконструируем трансформатор заданной мощности с возможным диапазоном изменения напряжений на первичной и вторичной обмотках. В качестве ограничений учтем требования по допустимым потерям холостого хода и работе на линейной части характеристики намагничивания сердечника и габаритам трансформатора.
В этом случае необходимо учитывать электрические, магнитные, конструктивные, геометрические, тепловые свойства трансформатора.
Вводить понятие модели без четкого указания задачи или задач неправомерно. Вне контекста задачи или класса задач понятие модели не имеет смысла.
Фундаментальным свойством модели является простота по отношению к объекту. Модель всегда «беднее» объекта в информационном отношении. «Точная модель» недоступна, как и сам оригинал.
Задача своими условиями и требованиями позволяет определить ограничения и допущения в построении любой модели.
Пример 2. Рассмотрим маятник – груз, подвешенный на нити. Модель (геометрическая) дана на рис. 1.2. Модель (математическая) движения маятника в общем является довольно сложным нелинейным дифференциальным уравнением, но при принятых допущениях, «дозволенных» задачей, это уравнение становится достаточно простым и легко решается. Перечислим допущения, которые принимаются при этом:
· размерами маятника пренебрегаем, и его масса сосредоточена в одной точке (пренебрегаем сопротивлением воздуха);
· растяжением нити пренебрегаем;
· массой нити пренебрегаем.
Вводится также ограничение: амплитуда колебаний пренебрежимо мала по сравнению с длиной нити.
При таких допущениях и ограничениях получается модель – математический маятник. Период малых колебаний математического маятника не зависит от массы маятника и амплитуды его колебаний. Уравнение движения маятника записывается в виде
,
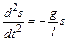где s – длина дуги, по которой маятник совершает движение; g – ускорение свободного падения; l – длина нити.
Как известно, наблюдения над колебаниями маятников используются для определения ускорения g силы тяжести в разных широтах земного шара.
Человечество за свою жизнь накопило огромное количество теорий и законов. Это практически достоверное обобщенное описание объектов реального мира.
Иногда для решения частных задач вводятся еще большие ограничения и допущения, которые упрощают известные теории и законы. В этом случае появляются модели моделей, в которые переходят все допущения и ограничения исходных моделей.
Классификация моделей
Существуют разные способы классификации моделей:
· по классам задач;
· по области использования;
· по способу представления и др.
Из классов задач, по которым разделяют модели, можно назвать: анализ, синтез, конструирование, проектирование, управление, утилизация и т. п.
По области использования модели разделяют:
· учебные – наглядные пособия, различные тренажеры, обучающие программы;
· опытные – копии объектов, которые используются для исследования объекта и прогнозирования его характеристик в будущем;
· научно-технические, используемые для исследования процессов и явлений (различные стенды, моделирующие физические и природные явления);
· игровые – военные, экономические, спортивные и деловые игры;
· имитационные, которые моделируют с той или иной точностью работу объекта в различных условиях и, как правило, с учетом случайных факторов. Алгоритм (компьютерная программа), реализующий имитационную модель, воспроизводит процесс функционирования системы во времени, причем имитируются элементарные события, составляющие процесс, с сохранением их логической структуры и последовательностью протекания во времени. Это позволяет по исходным данным получить сведения о состоянии процесса в определенные моменты времени, дающие возможность оценить характеристики системы. Примером имитационной модели может служить программа расчета аварийного переходного процесса в электроэнергетической системе, когда во время протекания процесса имитируются события срабатывания различной автоматики и коммутации оборудования системы.
Способ представления модели – наиболее важный признак классификации моделей.
Все модели можно разделить на две группы: материальные и идеальные (информационные). В свою очередь физические модели разделяют на физические, аналоговые и геометрически подобные (макеты) (рис. 1.3).
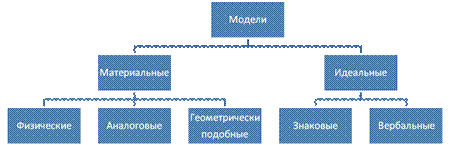
Рис. 1.3. Классификация моделей по способу представления
Физические модели имеют ту же природу, что и моделируемые объекты. Это, как правило, уменьшенные копии объектов, сохраняющие его основные физические свойства. Так, например, работу гидравлической турбины можно исследовать на лабораторной установке, воспроизводящей в масштабе настоящую турбину. Исследование работы генератора электростанции также можно выполнить на малой электрической машине переменного тока. Модели автомобилей, судов, самолетов, луноходов и других машин, которые являются физическими моделями, помогают инженерам исследовать механические, тепловые, электрические, магнитные, химические и другие свойства различных машин.
Иногда исследования проводятся на моделях, которые имеют отличную от исходного объекта физическую природу. Так, механические свойства движения вращающегося объекта (вала) можно исследовать на электрической модели, и, наоборот, токи и напряжения электрической цепи можно моделировать с помощью сил и скоростей элементов механической системы. Такие модели называют аналоговыми. Получило развитие направление моделирования с помощью специальных аналоговых вычислительных машин (АВМ), в отличие от цифровых вычислительных машин (ЦВМ).
Многие физические и аналоговые модели исследуются в динамике, т. е. изменении их параметров и свойств во времени. Моделирование предусматривает масштабирование не только по переменным модели, но и по времени; таким образом, процессы, протекающие в моделях, воспроизводятся в замедленном или ускоренном движении.
Геометрически подобные модели – это макеты зданий, сооружений и природных объектов. Они изготавливаются для решения учебных, архитектурных, экологических и инженерных задач.
Идеальные модели носят информационный характер. Они возникают и строятся в сознании людей и используются как любая информация. Можно сказать, что информация – это модель окружающего нас мира. Идеальные модели в зависимости от средств их изображения, передачи, хранения и использования подразделяются на знаковые и вербальные.
Знаковые модели используют какой-либо формализованный язык – литературный, математический, алгоритмический и др. Вербальными можно считать образные модели в сознании людей и передаваемые ими посредством разговорной речи.
Знаковые и вербальные модели взаимосвязаны. Мысленный образ, родившийся в мозгу человека, может быть облечен в знаковую форму, и, наоборот, знаковая модель позволяет сформировать в сознании верный мысленный образ.
Знаковые модели, записанные на каком-либо носителе (бумажном, магнитном, электрическом, оптическом и др.), передаются между людьми, обрабатываются на компьютерах и сохраняются для следующих поколений. В зависимости от этого можно выделить несколько видов знаковых моделей: дескриптивные, имитационные, алгоритмические, математические, базы данных и знаний.
Математическое представление об объекте должно согласовываться с возможностью дальнейшего анализа и исследования объекта по его математической модели. Каждый объект и система могут моделироваться на разных иерархических уровнях восприятия человеком окружающего мира. Принято разделять моделирование технических объектов по трем уровням: микро-, макро- и метауровень. На каждом из этих уровней применимы свои классы моделей, различающиеся главным образом представлением пространства и времени. Описание моделей разных иерархических уровней дано в разд. 1.6–1.8.