Метод решения определенного интеграла от нечетной функции по симметричному относительно нуля отрезку

Вам понравится. Рассмотрим тот же определенный интеграл с симметричным относительно нуля отрезком интегрирования:

.

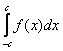Если подынтегральная функция f(x) является нечётной, то

.

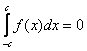Почему такой интеграл равен нулю?

Пример 6

Вычислить определенный интеграл

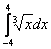
Выполним чертеж:

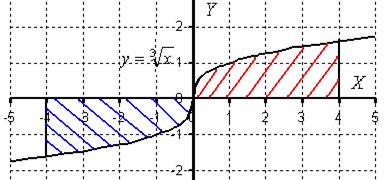
Вот, заодно и график функции 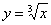, который ещё нигде у нас не встречался, график представляет собой перевёрнутую кубическую параболу.

Проверим нашу функцию на четность/нечетность:

,

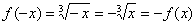значит, данная функция является нечётной, и её график симметричен относительно начала координат. Из симметрии графика следует равенство площадей, которые заштрихованы красным и синим цветом.

При вычислении определенного интеграла

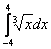
площадь, которая заштрихована синим цветом, формально является отрицательной. А площадь, которая заштрихована красным цветом – положительной. Поскольку площади равны и формально противоположны по знаку, то они взаимно уничтожаются, следовательно

.

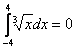И еще раз подчеркиваем разницу между заданиями:

1) Любой определенный интеграл (само собой он должен существовать) – это всё равно формально площадь(пусть даже отрицательная). В частности, поэтому

,

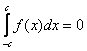так как в силу нечётности функции 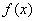площади взаимно уничтожатся. Что и проиллюстрировано на конкретном примере.

2) Задача на нахождение площади – это совершенно другая задача. Так, если нам предложено найти площадь фигуры в данном примере, то её следует вычислить, как:

.

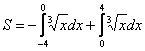Еще несколько коротких примеров на тему данного правила:

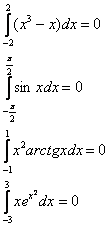
И, аналогично для любой нечетной функции и симметричного относительно нуля отрезка.

Применять ли данный метод на практике? На самом деле вопрос не такой простой. Когда вам предложен сложный пример с большим количеством вычислений, то можно, и даже уместно указать, что такой интеграл равен нулю, сославшись на нечетность функции и симметричность отрезка интегрирования относительно нуля.

Как говорится, знание – сила, а незнание – рабочая сила.

Но когда вам предложен короткий пример, то преподаватель вполне обоснованно может заставить прорешать его подробно: взять интеграл и подставить пределы интегрирования по формуле Ньютона-Лейбница. Всё зависит от постановки задачи. Например, Вам предложено вычислить тот же неопределенный интеграл

.

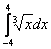Если вы сразу запишите, что

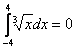
и поясните словами, почему получается ноль, то это будет не очень хорошо, поскольку перед Вами стояла задача вычислить. Намного лучше «прикинуться дурачком» и провести полное решение:

.

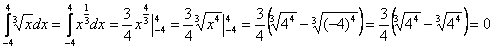То, что интеграл равен нулю, вы будете знать заранее. И это знание 100 %-но позволит избежать ошибки.

С другой стороны, когда в тестовом задании спрашивают: «Чему равен интеграл?», то отвечать нужно быстро, на основе всего, что знаешь по этому вопросу.