Задания для практических занятий
1. 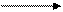   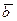 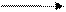 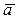 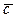 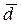 | Вспомнить понятия коллинеарности, компланарности. 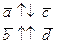 , , 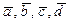 - компланарны - компланарны | ||
| 2.
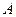 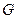 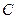 | 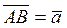 , , 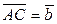 , , 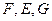 - середины соответствующих сторон треугольника АВС. Выразить через - середины соответствующих сторон треугольника АВС. Выразить через 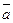 и и 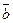 векторы векторы 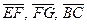 . . | ||
     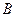 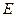 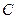    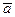 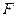 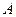 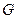 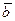 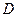 | 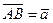 , , 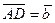 , , 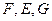 - середины сторон параллелограмма ABCD - середины сторон параллелограмма ABCD 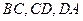 соответственно. Выразить через соответственно. Выразить через 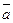 и и 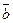 векторы векторы 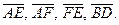 | ||
   4 4 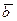   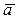 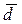 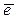 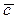 | Выразить каждый из векторов 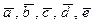 через остальные. через остальные. | ||
5.         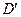 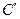   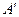 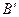 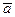 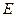 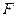 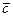 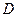 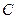 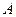 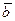 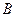 | 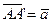 , , 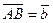 , , 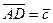 , , 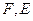 - середины сторон параллелепипеда - середины сторон параллелепипеда 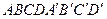 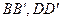 соответственно. Выразить через соответственно. Выразить через 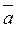 , , 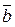 и и 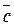 векторы векторы 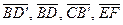 . . | ||
6.       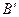 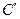  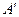 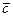 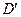   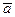 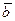 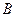 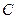 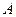 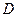 | В параллелепипеде 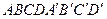 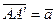 , , 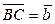 , , 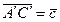 . Выразить через . Выразить через 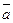 , , 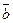 и и 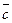 векторы векторы 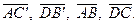 | ||
7.   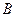 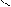 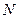 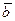 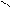 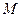  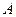 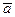 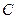 | В треугольнике АВС 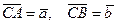 . Известно, что: . Известно, что: 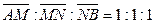 . Выразить вектор . Выразить вектор 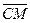 через через 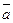 и и 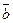 . . | ||
8.     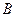 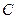  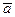  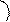  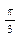 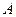 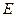 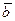  | В параллелограмме ABCD 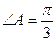 , , 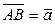 , , 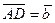 . Выразить через . Выразить через 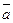 и и 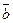 векторы векторы 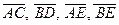 . . | ||
9.   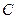  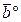   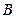 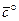 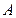 | В прямоугольном треугольнике АВС: 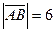 , , 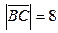 . Выразить через . Выразить через 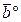 и и 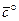 векторы векторы 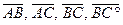 . . | ||
10.  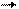 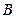 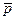 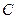    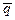   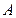 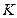 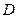 | В трапеции ABCD 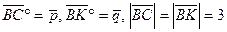 , , 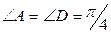 . Выразить через . Выразить через 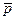 и и 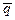 векторы векторы 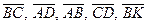 . . |
11. Вычислить модуль вектора 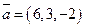 .
.
12. Вычислить модуль и орт вектора 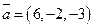 .
.
13. Вычислить направляющие косинусы вектора 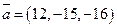 .
.
14. Дан модуль вектора 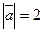 и его направляющие косинусы:
и его направляющие косинусы: 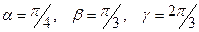 . Вычислить проекции вектора на координатные оси.
. Вычислить проекции вектора на координатные оси. 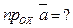
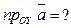
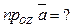
15. При каких значениях 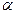 и
и 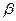 векторы
векторы 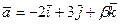 и
и 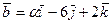 коллинеарные?
коллинеарные?
16. Дан вектор 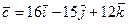 . Векторы
. Векторы 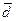 и
и 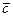 коллинеарные. Модуль вектора
коллинеарные. Модуль вектора 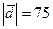 . Найти координаты вектора
. Найти координаты вектора 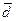 .
.
17. Показать, что векторы 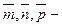 компланарные:
компланарные:
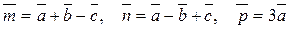 .
.
18. Показать, что 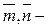 коллинеарные:
коллинеарные:
a) 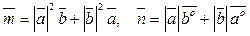 ,
,
б) 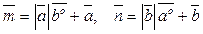 .
.
19. В треугольнике 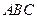 точка
точка 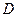 делит сторону
делит сторону 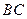 в отношении 2 к 3 , считая от вершины
в отношении 2 к 3 , считая от вершины 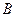 . Найти координаты вектора
. Найти координаты вектора 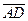 в базисе
в базисе 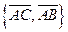 .
.
20. Даны векторы: 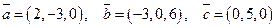 .
.
а) показать, что 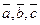 - базис,
- базис,
б) найти координаты вектора 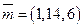 в базисе
в базисе 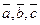 ,
,
в) найти координаты вектора 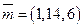 в базисе
в базисе 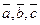 .
.
21. Дано: 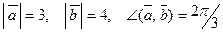 . Вычислить:
. Вычислить:
а) 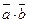 , б)
, б) 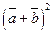 , в)
, в) 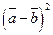 , г)
, г) 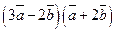 , д)
, д) 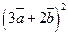 .
.
22. Дано: 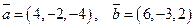 . Вычислить:
. Вычислить:
а) 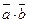 , б)
, б) 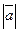 , в)
, в) 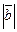 , г)
, г) 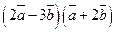 ,
,
д) 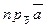 , е)
, е) 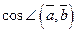 .
.
23. Найти координаты вектора 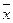 , если
, если 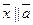 ,
, 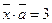 ,
, 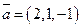 .
.
24. Дано: 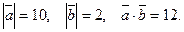 Найти
Найти 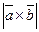 .
.
25. Дано: 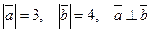 . Вычислить:
. Вычислить:
а) 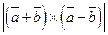 , б)
, б) 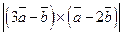 .
.
26. Дано: 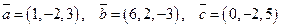 . Вычислить:
. Вычислить:
а) 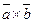 , б)
, б) 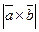 , в)
, в) 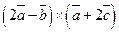 , г)
, г) 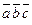 .
.
27*. Дано: 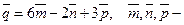 взаимно перпендикулярные орты. Найти
взаимно перпендикулярные орты. Найти 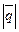 .
.
28*. Найти проекцию вектора 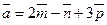 на вектор
на вектор 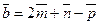 , где
, где 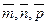 - взаимно перпендикулярные орты.
- взаимно перпендикулярные орты.
29*. Вычислить площадь параллелограмма, построенного на векторах 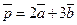 и
и 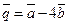 где
где 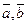 - взаимно перпендикулярные орты.
- взаимно перпендикулярные орты.
30*. Упростить: 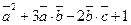 , где
, где 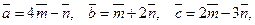
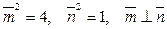
31*. Вычислить 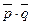 , если
, если 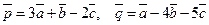 ,
, 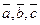 - взаимно перпендикулярные орты.
- взаимно перпендикулярные орты.
32*. Вычислить длину вектора 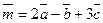 , если
, если 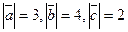 ,
, 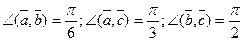 .
.
33**. Дано: 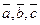 - правая тройка, векторы взаимно перпендикулярны,
- правая тройка, векторы взаимно перпендикулярны, 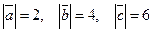 . Выразить каждый из векторов через векторное произведение двух других.
. Выразить каждый из векторов через векторное произведение двух других.
34**. Найти проекцию вектора 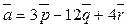 на вектор
на вектор  , где
, где 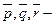 взаимно перпендикулярные орты.
взаимно перпендикулярные орты.
35**. Вычислить площадь треугольника, построенного на векторах 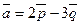 и
и 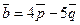 , где
, где 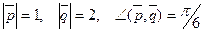 .
.
36**. Найти угол между векторами 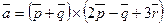 и
и 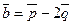 , если
, если 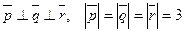 .
.
37**. Упростить вектор 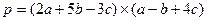 , где
, где 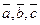 - левая тройка, векторы взаимно перпендикулярны,
- левая тройка, векторы взаимно перпендикулярны, 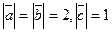 .
.
38**. Найти объем параллелепипеда, построенного на векторах 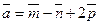 ,
, 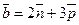 ,
, 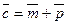 , где
, где 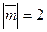 ,
, 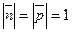 ,
, 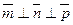 .
.
39**. Вычислить длину медианы треугольника АВС, проведенной из вершины 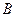 , если
, если 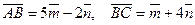 , где
, где 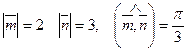 .
.
40**. Вычислить длину высоты треугольника АВС, опущенную из вершины 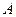 , если
, если 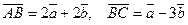 , где
, где 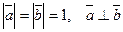 .
.
ОТВЕТЫ
Векторная алгебра
2. 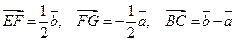 ;
;
3. 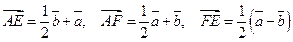 ,
, 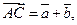
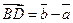 ;
;
4. 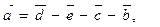
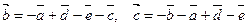 ,
, 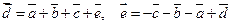 ;
;
5. 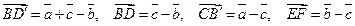 ;
;
6. 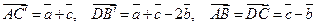 ;
;
7. 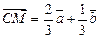 ;
;
8. 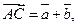
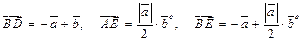 ;
;
9. 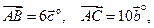
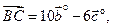
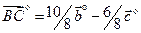 ;
;
10. 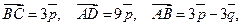
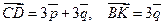 ;
;
11. 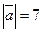 ; 12.
; 12. 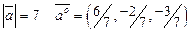 ;
;
13. 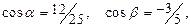
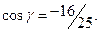 ;
;
14. 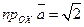 ,
, 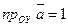 ,
, 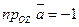 ; 15.
; 15. 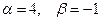 ;
;
16. 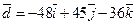 ; 17.
; 17. 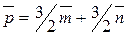 ;
;
18. a) 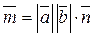 ; б)
; б) 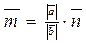 ;
;
19. 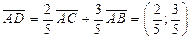 ;
;
20. a) 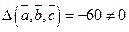 ; б)
; б) 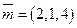 в базисе
в базисе 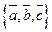 ; в)
; в) 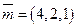 в базисе
в базисе 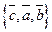 ;
;
21. а) 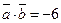 ; б)
; б) 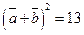 ; в)
; в) 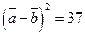 ;
;
г) 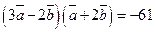 ; д)
; д) 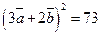 ; 22. а)
; 22. а) 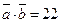 ;
;
б) 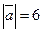 ; в)
; в) 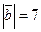 ; г)
; г) 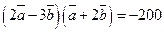 ; д)
; д) 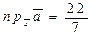 ;
;
е) 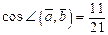 ; 23.
; 23. 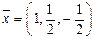 ; 24.
; 24. 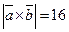 ;
;
25. а) 24; б) 60;
26. а) 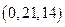 ; б)
; б) 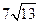 ;
;
в) 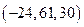 ; г) 28;
; г) 28;
27. 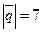 ; 28.
; 28. 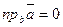 ; 29.
; 29. 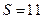 ; 30. 104;
; 30. 104;
31. 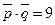 ; 32.
; 32. 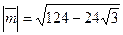 ;
;
33. 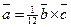 ,
, 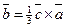 ,
, 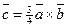 ;
;
34. 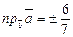 ; 35.
; 35. 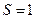 ;
;
36. 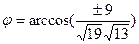 ; 37.
; 37. 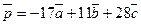 ;
;
38. 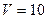 ; 39.
; 39. 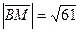 ; 40.
; 40. 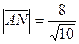 .
.




