Определение.Если решение системы линейных уравнений единственно, то она называется определённой, если не единственно, то неопределённой.

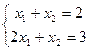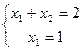Определённая: экв. решение (1,1).

Неопределённая: 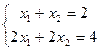Решения: (1,1) или (2,0) или (0,2) или (3,-1) или (4,-2), их бесконечно много.

Фактически 2-е уравнение лишнее, а из 1-го следует 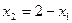. Что бы мы ни подставляли вместо 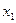, найдётся 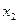. Единственного точного решения как такового здесь нет, их бесконечно много. Запись 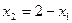здесь называется общим решением, а переменная 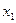, которую перенесли вправо и можем свободно задавать - свободной переменной.

* Если ранг основной матрицы меньше, чем число неизвестных, т.е. 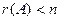то система неопределённая, так как есть столбцы, не входящие в базисный минор, и именно эти неизвестные переносятся вправо.

Геометрический смысл при n=2.

Рассмотрим систему из 2 уравнений и 2 неизвестных: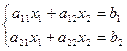

Её геометрический смысл. Каждое из уравнений задаёт некоторую прямую в плоскости. Прямые могут:

1. пересекаться в одной точке (решение единственно), в этом случае система совместная и определённая.

2. совпадать (решений бесконечно много), в этом случае система совместная, но неопределённая.

3. быть параллельны (нет решений) - система несовместна.

Методы решения систем с квадратной основной матрицей.

Матричный метод.

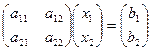, или 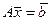. Слева домножим обратную матрицу:

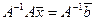, то есть 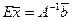, то есть 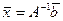. Получается, что все 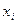можно найти так: умножить обратную матрицу на правую часть.

На примере: 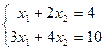. Матричный вид системы: 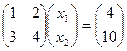, обратную матрицу для этой матрицы ранее находили, это 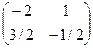. Тогда 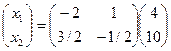= 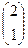. Итак, , .

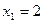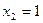Метод Крамера.

Пусть А - основная матрица системы линейных уравнений. Если удалить какой-либо i-й столбец основной матрицы и внести на это место правую часть, то получится некая новая квадратная матрица, обозначим её 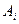. Тогда верны следующие формулы для 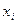. 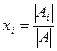для каждого i от 1 до n.

Идея доказательства формул Крамера проста и основывается на подробной записи матричного равенства 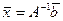, учитывая структуру обратной матрицы:

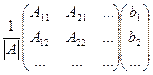тогда 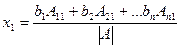как видим, алгебраические дополнения здесь именно к элементам 1-го столбца, но умножаются они на 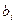, то есть, как если бы вместо 1-го столбца была поставлена правая часть системы.

Рассмотрим на примере той же самой системы: .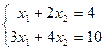

, .

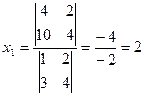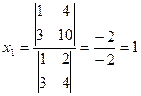Но эти два способа используются чаще для матриц 2 и 3 порядка, и они очень трудоёмкие, если матрица порядка 4 и больше.

Метод Гаусса.

Метод состоит в преобразовании основной матрицы к треугольному виду. Можно последовательно обнулить элементы ниже углового 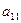, вычитая из других уравнений 1-е, домноженное на коэффициент 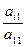(для каждой строки разные). Теперь 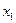будет только в первом уравнении, в других нет. Затем так же точно можем обнулить всё ниже чем 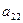, вычитая из каждой строки 2-ю с соответствующим коэффициентом. Кстати, при этом нули, уже расположенные слева, не изменятся. Затем обнулим все элементы ниже 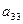, ниже 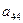, и так далее. В итоге для основной матрицы системы получится треугольный вид: нули везде ниже главной диагонали. При преобразованиях можно работать с расширенной матрицей, а не системой, чтобы не переписывать каждый раз 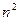букв « 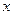». Обратите внимание, что правая часть подвергается тем же преобразованиям, что и вся строка, где находится этот .

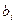После преобразований надо восстановить полную запись системы с неизвестными, но в ней уже будет хорошее свойство: чем ниже уравнение, тем меньше переменных, а в последнем вообще одна лишь 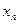. Это и позволит нам сначала выразить 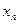, затем с этой известной информацией подняться в предпоследнее уравнение, и найти

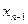, и так дажее до 1-го уравнения, где найдём .

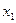На примере. 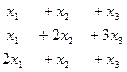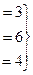Преобразования расширенной матрицы:

.

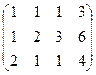
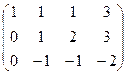
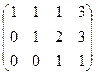Сначала из 2-й строки вычли 1-ю, а из 3-й удвоенную 1-ю.

На втором этапе, к 3-й прибавили 2-ю.

Система после преобразований:

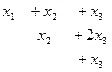
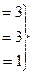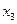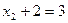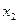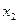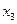, из последнего = 1, подставляем в предпоследнее, будет , то есть =1. Далее, уже известные и подставми в первое уравнение, и получим 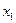=1.

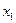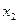Ответ =1, =1, 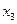= 1, или .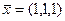