Совместность однородной системы

Рассмотрим однородную систему

.

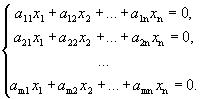Однородная система всегда совместна, так как всегда имеет тривиальное (нулевое) решение 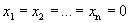. Выясним, когда данная система имеет нетривиальное решение.

Теорема 1. Однородная система имеет нетривиальное решение тогда и только тогда, когда ранг матрицы, составленной из коэффициентов при неизвестных, меньше числа неизвестных.

Доказательство. Пусть система совместна. Это может быть тогда и только тогда, когда найдутся числа с₁, с₂, …, с_n, при подстановке которых в систему мы получим mтождеств. Эти m тождеств можно записать в виде

.

Следовательно, система векторов-столбцов матрицы А линейно зависима. А это может быть тогда и только тогда, когда ранг системы векторов-столбцов меньше n, т.е. r(A)<n.

Следствие. Квадратная однородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы, составленной из коэффициентов при неизвестных, равен нулю.

Доказательство. Так как r(A)<n, то столбцы матрицы линейно зависимы и, следовательно, определитель матрицы равен нулю.

№17

Основные определения.

Пусть К – поле. Элементы поля К мы будем называть скалярами. Под полем К можно понимать или поле действительных чисел или поле комплексных чисел.

Определение. Матрицей размера 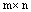над полем К называется таблица элементов поля К, имеющую 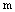строк и 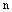столбцов.

Обозначение:

.

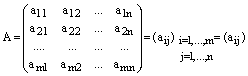Определение. Элементы 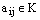называются элементами матрицы, где i – номер строки, в которой находится элемент 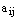, j – номер столбца.

Определение. Матрица размеров :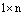

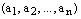называется строкой длины .

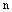Определение. Матрица размеров :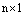

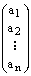называется столбцом высоты .

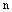Определение. Матрица размеров 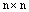называется квадратной матрицей 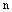– го порядка.

Определение. Матрица, все элементы которой равны нулю, называется нулевой.

В квадратной матрице выделяют две диагонали, как диагонали квадрата: главную диагональ и побочную диагональ.

Главную диагональ образуют элементы 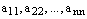, т.е. элементы с одинаковыми нижними индексами.

Побочную диагональ образуют элементы .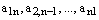

Определение. Квадратная матрица, в которой все элементы вне главной диагонали равны 0, называется диагональной:

.

Определение. Матрица В размера 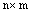называется транспонированной по отношению к матрице А размера 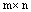, если к – й столбец матрицы В состоит из элементов к – й строки матрицы А, для всех .

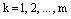Обозначение: .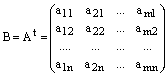

Определение. Процесс (процедура) получения транспонированной матрицы из данной называется транспонированием матрицы.

Пример:

, .

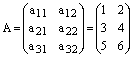Определение. Две матрицы 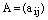и 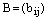называются равными, если они имеют одинаковые размеры и для всех значений индексов выполняется равенство .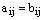