Түйіндес бейнелеудің қасиеттері.
Теорема 5. Егер 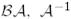 немесе
немесе 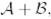 бейнелеуі анықталса, онда келесі теңдіктер орынды болады:
бейнелеуі анықталса, онда келесі теңдіктер орынды болады:
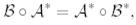 (26)
(26)
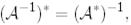 (27)
(27)
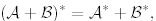 (28)
(28)
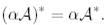 (29)
(29)
Евклид кеңістігіндегі түйіндес бейнелеу
Айталық 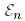 және
және 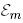 - евклид кеңістіктері болсын.
- евклид кеңістіктері болсын. 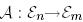 сызықтық бейнелеуін және
сызықтық бейнелеуін және 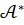 түйіндес бейнелеуін қарастырайық. Евклид кеңістігінің маңызды ерекше белгісі, бұл – оны оған түйіндес кеңістікпен теңестіруге болады. Мұндай теңестіру базистің таңдауына тәуелсіз
түйіндес бейнелеуін қарастырайық. Евклид кеңістігінің маңызды ерекше белгісі, бұл – оны оған түйіндес кеңістікпен теңестіруге болады. Мұндай теңестіру базистің таңдауына тәуелсіз 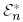 және
және 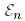 кеңістіктерінің изоморфизмі болатындығынан шығады.
кеңістіктерінің изоморфизмі болатындығынан шығады.
Теорема 6. Евклид кеңістігі өзінің түйіндес кеңістігіне эквивалентті. Яғни 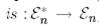 изоморфизмі бар болады, ол әрбір
изоморфизмі бар болады, ол әрбір 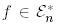 функциясына
функциясына 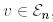 векторын сәйкес қояды, сонымен қатар
векторын сәйкес қояды, сонымен қатар
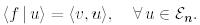 (30)
(30)
Дәлелдеу. Айталық 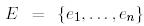 -
- 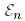 кеңістігінің берілген базисі болсын. Кез келген
кеңістігінің берілген базисі болсын. Кез келген 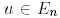 векторы үшін оның Е базисі бойынша жіктелуі :
векторы үшін оның Е базисі бойынша жіктелуі :
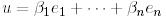 (31)
(31)
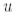 векторының Е базисіндегі координат бағанын анықтайды:
векторының Е базисіндегі координат бағанын анықтайды:
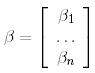 .
.
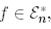 сызықтық функциясын қарастырайық және айталық
сызықтық функциясын қарастырайық және айталық 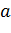 - Е базисіндегі осы функцияның вектор-жолы болсын, ол (4) формулаға сәйкес
- Е базисіндегі осы функцияның вектор-жолы болсын, ол (4) формулаға сәйкес 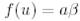 болады.
болады.
Е базисіндегі 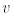 векторының координаттық бағанын
векторының координаттық бағанын
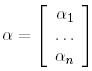
деп белгілейік.
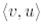 скаляр көбейтіндіні координаттық формада жазайық:
скаляр көбейтіндіні координаттық формада жазайық:
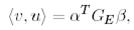 (32)
(32)
мұндағы 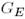 - Е базисіндегі Грам матрицасы.
- Е базисіндегі Грам матрицасы.
Ары қарай, (4) сәйкес 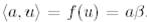 болады. (30)-ды координаттық формада жазайық:
болады. (30)-ды координаттық формада жазайық:
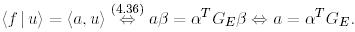
Е базисіндегі 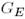 Грам матрицасы ерекше емес болғандықтан, онда соңғы теңдікті
Грам матрицасы ерекше емес болғандықтан, онда соңғы теңдікті 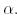 -ға қатысты шешуге болады.
-ға қатысты шешуге болады. 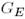 Грам матрицасының симметриялылығынан мынаны аламыз:
Грам матрицасының симметриялылығынан мынаны аламыз:
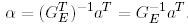 (33)
(33)
Мұнда 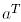 - Е базисіне ортогональ
- Е базисіне ортогональ 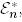 түйіндес кеңістіктің
түйіндес кеңістіктің 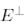 базисіндегі
базисіндегі 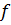 функциясының координаттық бағаны. Сонымен, (33)-тен
функциясының координаттық бағаны. Сонымен, (33)-тен 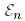 және
және 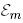 кеңістіктері изоморфты болатындығы шығады.
кеңістіктері изоморфты болатындығы шығады.
Осылайша, евклид кеңістігі өзінің түйіндес кеңістігіне изоморфты. Сондықтан да, 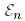 евклид кеңістігін оған түйіндес
евклид кеңістігін оған түйіндес 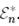 кеңістігіне теңестіруге болады.
кеңістігіне теңестіруге болады.
Анықтама 7.
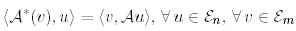 (34)
(34)
теңдігімен анықталатын 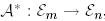 бейнелеуі
бейнелеуі 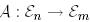 бейнелеуіне түйіндес деп аталады.
бейнелеуіне түйіндес деп аталады.
Теорема 7. Егер 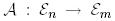 бейнелеуі ортонормаланған базисте А матрицасына ие болса, онда сол базистегі оның
бейнелеуі ортонормаланған базисте А матрицасына ие болса, онда сол базистегі оның 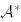 түйіндес бейнелеуі
түйіндес бейнелеуі 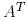 матрицасына ие болады.
матрицасына ие болады.
Мысал 7. (Евклид кеңістігінің түйіндес бейнелеуінің матрицасы). 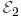 және
және 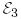 екі евклид кеңістіктерін және олардың
екі евклид кеңістіктерін және олардың 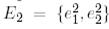 және
және 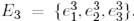 ,
, 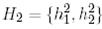 және
және 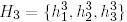 базистерін қарастырайық, сонымен қатар,
базистерін қарастырайық, сонымен қатар, 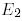 және
және 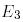 - ортонормаланған, ал
- ортонормаланған, ал 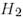 және
және 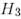 базистері
базистері 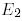 және
және 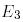 базистерімен төмендегі қатынастар арқылы байланысқан:
базистерімен төмендегі қатынастар арқылы байланысқан:
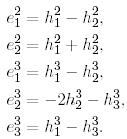
Бұдан 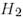 базисінен
базисінен 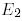 базисіне көшу
базисіне көшу 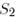 матрицасы мына түрге ие болады:
матрицасы мына түрге ие болады:
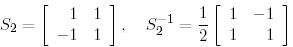
ал 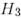 базисінен
базисінен 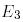 базисіне көшу
базисіне көшу 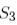 матрицасы былай болады:
матрицасы былай болады:
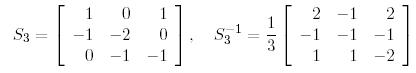
Айталық 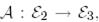 сызықтық бейнелеуі
сызықтық бейнелеуі 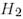 және
және 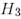 базистерінде
базистерінде
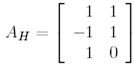
түріне ие болсын.
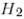 және
және 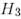 базистерінде
базистерінде 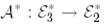 түйіндес бейнелеудің матрицасын табайық.
түйіндес бейнелеудің матрицасын табайық.
Алдымен 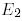 және
және 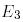 базистеріндегі
базистеріндегі  бейнелеуінің матрицасын табайық:
бейнелеуінің матрицасын табайық:
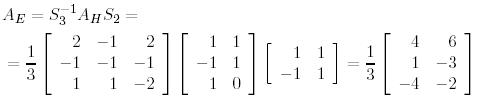 .
.
 және
және  базистері ортонормаланған болғандықтан, онда 7-теоремаға сәйкес осы базистегі түйіндес бейнелеудің
базистері ортонормаланған болғандықтан, онда 7-теоремаға сәйкес осы базистегі түйіндес бейнелеудің  матрицасы мына түрге ие болады:
матрицасы мына түрге ие болады:
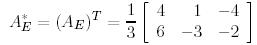 .
.
Онда 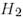 және
және 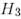 базистерінде түйіндес бейнелеудің
базистерінде түйіндес бейнелеудің 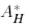 матрицасы келесі түрге ие болады:
матрицасы келесі түрге ие болады:
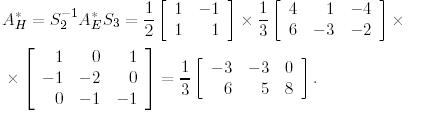
Дәріс 17,18
УНИТАР ЖӘНЕ ҚАЛЫПТЫ МАТРИЦАЛАР
