Неинерциальная система отсчёта
Нарисуем теперь неинерциальную систему координат связанную с наблюдателем, которая в каждый момент времени по часам наблюдателя совпадает с системой, относительно которой наблюдатель неподвижен. Т.е. от каждой мгновенной системы наблюдатель берёт лишь множество одновременных ему точек — ось 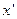 .
.
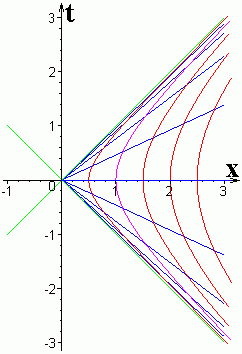 На рисунке изображены линии постоянных значений координаты
На рисунке изображены линии постоянных значений координаты 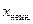 и времени
и времени 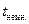 для этой системы. Линии
для этой системы. Линии 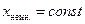 — дуги гипербол.
— дуги гипербол. 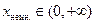 , гиперболы на рисунке соответствуют значениям +0,5, +1, +1,5, +2, +2,5. Линии
, гиперболы на рисунке соответствуют значениям +0,5, +1, +1,5, +2, +2,5. Линии 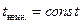 — лучи выходящие из начала координат и имеющие коэффициент наклона от –1 до +1. Какое именно время приписать каждому из этих лучей зависит от того, чему равна координата
— лучи выходящие из начала координат и имеющие коэффициент наклона от –1 до +1. Какое именно время приписать каждому из этих лучей зависит от того, чему равна координата 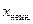 точки, в которой находятся часы. На рисунке предполагалось, что для часов
точки, в которой находятся часы. На рисунке предполагалось, что для часов 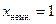 (соответствующая гипербола выделена цветом). Лучи на рисунке соответствуют значениям времени по этим часам равным –2, –1,5, –1, –0,5, 0, +0,5, +1, +1,5, +2.
(соответствующая гипербола выделена цветом). Лучи на рисунке соответствуют значениям времени по этим часам равным –2, –1,5, –1, –0,5, 0, +0,5, +1, +1,5, +2. 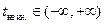 .
.
Почему мы ограничили диапазон изменения 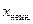 положительной полуосью? Для этого есть два объяснения: 1) неинерциальную систему нельзя продолжить за пределы той ¼ плоскости на которой мы её определили т.к. на границе этой области система становится особой (при приближении к лучам
положительной полуосью? Для этого есть два объяснения: 1) неинерциальную систему нельзя продолжить за пределы той ¼ плоскости на которой мы её определили т.к. на границе этой области система становится особой (при приближении к лучам 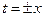 время наблюдателя
время наблюдателя 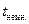 стремится к
стремится к 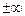 ), 2) область отрицательных
), 2) область отрицательных 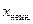 (1/4 плоскости симметричная к рассматриваемой) недоступна для наблюдения равноускоренного наблюдателя, а наблюдатель не в состоянии на неё повлиять, если влияние (сигнал) не может передаваться быстрее скорости света.
(1/4 плоскости симметричная к рассматриваемой) недоступна для наблюдения равноускоренного наблюдателя, а наблюдатель не в состоянии на неё повлиять, если влияние (сигнал) не может передаваться быстрее скорости света.
На этом стоит остановиться подробнее ещё и потому, что здесь снова прослеживается связь с ОТО. На этот раз мы сможем увидеть на том же рисунке некоторые свойства похожие на те, что наблюдаются вблизи «поверхности» (на самом деле это не поверхность, а «горизонт событий») чёрной дыры. Чёрная дыра — это такая область пространства-времени, что никакой сигнал (включая световой) не может выйти из неё наружу (к удалённому наблюдателю). Граница этой области — горизонт событий. С точки зрения удалённого наблюдателя (который на дыру не падает) для того, чтобы достичь горизонта событий любому предмету требуется бесконечное время, однако, наблюдатель, который сам падает в чётную дыру обнаружит, что по его часам горизонт был достигнут за конечное время. В нашем случае горизонт событий — лучи 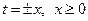 . На этих лучах
. На этих лучах 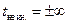 ,
, 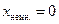 . По часам ускоренного наблюдателя если предмет, который он наблюдает пытается пересечь линию
. По часам ускоренного наблюдателя если предмет, который он наблюдает пытается пересечь линию 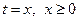 , т.е. летит к точке
, т.е. летит к точке 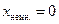 , то для достижения этой точки ему потребуется бесконечное время, в то время как часы самого предмета при
, то для достижения этой точки ему потребуется бесконечное время, в то время как часы самого предмета при 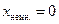 покажут конечное время (см. рассматривавшийся выше эффект замедления времени в гравитационном поле). Как и в случае горизонта чёрной дыры предмет пересекший линию
покажут конечное время (см. рассматривавшийся выше эффект замедления времени в гравитационном поле). Как и в случае горизонта чёрной дыры предмет пересекший линию 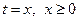 не сможет передать нашему наблюдателю никакой сигнал, т.к. для этого потребовалась бы скорость передачи сигнала превышающая скорость света.
не сможет передать нашему наблюдателю никакой сигнал, т.к. для этого потребовалась бы скорость передачи сигнала превышающая скорость света.
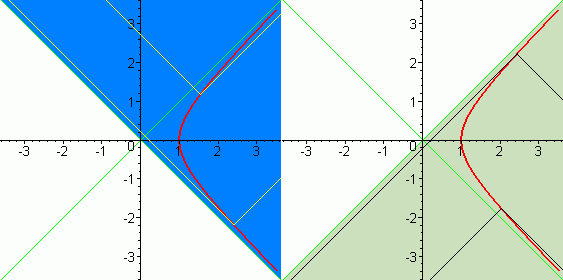
На левом рисунке изображена мировая линия равноускоренного наблюдателя и закрашены все те события, на которые он может влиять. Для прояснения картины для двух точек мировой линии изображены световые сигналы, посланные наблюдателем в разные стороны (это позволяет легче понять, как послать сигнал в любую точку закрашенной области).
На правом рисунке изображена мировая линия равноускоренного наблюдателя и закрашены все те события, которые могут влиять на наблюдателя. Для прояснения картины для двух точек мировой линии изображены световые сигналы, принятые наблюдателем с разных сторон (это позволяет легче понять, как принять сигнал из любой точки закрашенной области).
Из картинок видно, что на самом деле горизонтов не один, а два:
1) прямая 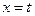 является горизонтом будущего, можно уйти от наблюдателя за эту линию, но обратно вернуться нельзя,
является горизонтом будущего, можно уйти от наблюдателя за эту линию, но обратно вернуться нельзя,
2) прямая 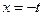 является горизонтом прошлого, можно прийти к наблюдателю из-за этой линии, но обратно вернуться нельзя.
является горизонтом прошлого, можно прийти к наблюдателю из-за этой линии, но обратно вернуться нельзя.
Такая же ситуация получается и при рассмотрении полного решения, описывающего чёрную дыру: там тоже два горизонта, один из которых — горизонт чёрной дыры за который можно упасть, но откуда нельзя выбраться, а другой — горизонт белой дыры, откуда можно вылететь, но куда нельзя вернуться (впрочем, белые дыры считаются неустойчивыми). Что будет если кто-то вылетев из белой дыры попробует вернуться обратно, через горизонт событий? Вместо того, чтобы вернуться в белую дыру он упадёт в чёрную. Аналогично на нашем рисунке вылетев из под линии 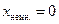 (пересекши линию
(пересекши линию 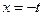 ) можно вернуться снова в точку, где
) можно вернуться снова в точку, где 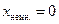 , но это будет уже линия
, но это будет уже линия 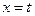 .
.
 |
Рисунок откуда-то из сети
