Составляем маршруты методом «совмещенной матрицы»
В соответствующие клетки матрицы груженых ездок из матрицы оптимального плана порожних ездок переносятся данные, характеризующие количество и направление возврата порожних автомобилей. Эти цифры, для их различия, запишем так: в левых верхних углах будем записывать холостые ездки, в правых нижних – груженые ездки. Таким образом будет построена таблица, которая называется «совмещенной матрицей».
| A | B | C | D | E | итого | |
| A | (50) | |||||
| B | ||||||
| C | (36) | (14) | (20) | (9) | (54) | |
| D | (21) | |||||
| E | ||||||
| итого |
В некоторых клетках таблицы появятся две записи: одна – характеризующая количество ездок в данном направлении, другая – возврат порожняка в обратном направлении. Меньшая цифра покажет мощность грузопотока по полученному маршруту.
| A | B | C | D | E | итого | |
| A | (50) | |||||
| B | ||||||
| C |   (36) (36) |   (14) (14) | (20) | (9) |  (54) (54)  33 33 | |
| D | (21) | |||||
| E | ||||||
| итого |
1 маршрут маятниковый С-А 36 ездок β=0,5
2 маршрут С-В маятниковый 14 ездок β=0,5
3 маршрут С-Е маятниковый 33 ездки β=0,5
После того, как будут выявлены все маятниковые маршруты, в клетках таблицы останется только по одной цифре, показывающей или количество груженых ездок, или количество холостых ездок, которое будет совершать подвижной состав в данном направлении.
Для каждой клетки таблицы, загруженной величиной объема перевозок груза, строится контур таким образом, чтобы все его четные углы лежали в клетках, загруженных количеством груженых ездок, а нечетные – в клетках, загруженных числом порожних ездок.
| A | B | C | D | E | итого | |
| A |  (50) (50) |  | ||||
| B | ||||||
| C |   |  (20) (20) | (9) | (21) | ||
| D | (21) | |||||
| E | ||||||
| итого |
4 маршрут С=В – B=A – А=С – С=C кольцевой 20 ездок β=0,74
| A | B | C | D | E | итого | |
| A |   (30) (30) |  | ||||
| B | ||||||
| C |   | (9) | (21) | |||
| D | (21) | |||||
| E | ||||||
| итого |
5 маршрут C=B –B=A – A=D – D=C кольцевой 9 ездок β=0,55
Полученные таким образом контуры покажут рациональные кольцевые маршруты движения подвижного состава. Мощность грузопотока на каждом из этих маршрутов будет определяться наименьшей величиной загрузки клеток, расположенных в углах контура. Затем по этим же правилам строятся контуры с учетом оставшихся величин загруженных клеток.
Построение контуров, а, следовательно, и выявление кольцевых и петлевых рациональных маршрутов продолжается до тех пор, пока не останется ни одной загруженной клетки.
| A | B | C | D | E | итого | |
| A |   (21) (21) |  | ||||
| B | ||||||
| C |   | (21) | ||||
| D |  (21) (21) |  | ||||
| E | ||||||
| итого |
6 маршрут С=B – B=A – A=D – D=E – E=C кольцевой маршрут 21 ездка
β=0,5
Для закрепления представленного материала, необходимо выполнить самостоятельную работу по заданию, указанному ниже.
Корреспонденция грузопотоков и объёмы перевозок
Таблица 1.1
| 1 цифра вари-анта задания | Грузопоток | 2 цифра вари-анта задания | Грузы | ||
| Из пункта | В пункт | Наименование | Днев. об., т | ||
| С А А D А С | А D Е В С В | Руда Уголь Щебень Известняк Порода Глина | |||
| D С А А С Е | В А D С В D | Мука Сахар Консервы Канцелярия Соки, воды Бакалея | |||
| С А D С С А | В С Е А А D | Грунт Глина Шлак Зола Керамзит Опилки | |||
| D А С Е С А | Е D А D В С | Лён-волокно Шерсть-тюки Шифер Бумага(рул) Доски Картофель | |||
| D А С С D А | В С В А С D | Сталь(рул) Двиг.электр. Зап.части авт. Тара мелкош. Покр. авт. Чугун | |||
| С А С А Е В | А С В D D Е | Битум Асфальт Щебень Грунт Бет. Блоки М-лом | |||
| А С D С А С | D А Е Е С В | Овощи Шифер Стен.панели Удобрения Животные Паллеты | |||
| А С А А С D | С В D D А В | Цемент Мел Битум Глина Скоб.изд Рубероид | |||
| С Е А С А В | А С D В С Е | Краска Фанера ДСП Опилки Шпон Лес кругляк | |||
| Продолжение табл.1.1 | |||||
| А А С А С В | D D А С В С | Кирпич Черепица Глина Пром.отходы Песок Пром.отходы |
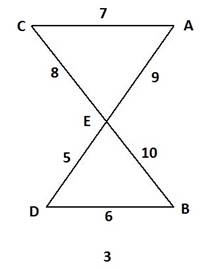
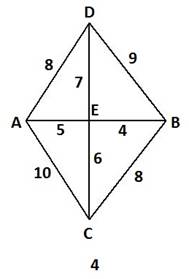
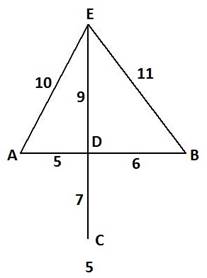
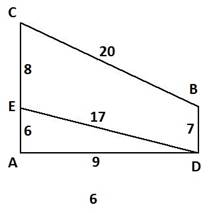
Схема дорожной сети (третья цифра варианта задания)
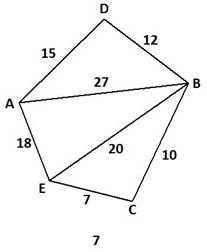
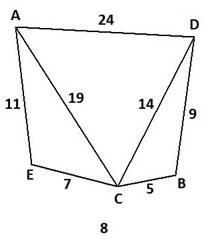
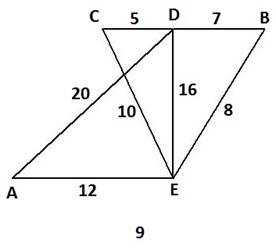
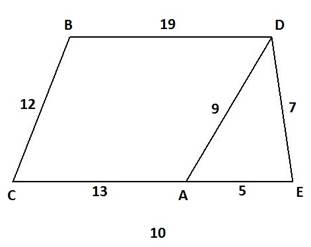
Библиографический список
3. Л.Г. Лавров. «Маршрутизация грузовых автомобильных перевозок», «НГТУ», НН. 2001.
