Контрольная работа № 5
| № варианта | Номера заданий |
| 25, 6, 18, 13 | |
| 1, 20, 14, 25 | |
| 24, 7, 17, 14 | |
| 2, 19, 13, 24 | |
| 23, 8, 18, 11 | |
| 3, 18, 12, 21 | |
| 22, 9, 17, 14 | |
| 4, 17, 15, 23 | |
| 21, 10, 1, 18 | |
| 5, 16, 11, 20 |
№ 1.Из колоды карт (36 листов) наугад достают одну карту. Пусть событие А состоит в том, что этой картой окажется какая-то из четырех дам. В – событие, состоящее в том, что извлеченная из колоды карта окажется черной масти. Найдите Р(А+В).
№ 2. Чему равна вероятность того, что число, взятое наугад из всех трехзначных чисел, делится хотя бы на одно из чисел 4 и 6.
№ 3. Вычислите вероятность того, что число, взятое наугад из всех трехзначных чисел, делится хотя бы на одно из чисел 4, 6 и 15.
№ 4. Вероятность того, что студент сдаст первый экзамен, равна – 0,9; второй – 0,9; третий – 0,8. Найти вероятность того, что студентом будут сданы: а) только второй экзамен; б) только один экзамен; в) три экзамена; г) по крайней мере два экзамена; д) хотя бы один экзамен.
№ 5. Причиной разрыва электрической цепи служит выход из строя элемента К1 или одновременный выход из строя двух элементов – К1, К3. Элементы могут выйти из строя независимо друг от друга с вероятностями, равными соответственно 0,1; 0,2; 0,3. Какова вероятность разрыва электрической цепи?
№ 6. Какова вероятность того, что при бросании десяти монет выпадет семь «гербов» и три «решки»?
№ 7.Бросают пять игральных костей. Чему равна вероятность того, что из пяти выпавших цифр одна – четная, а остальные – нечетные?
№ 8. Какова вероятность того, что при бросании семи игральных костей шестерка выпадет трижды?
№ 9.В лифт 9-этажного дома на 1-м этаже вошли 5 человек. Вычислите вероятность того, что на 6-м этаже не выйдет ни один из них.
№ 10.В лифт 9-этажного дома на 1-м этаже вошли 5 человек. Вычислите вероятность того, что на 6-м этаже выйдет один из них.
№ 11.В лифт 9-этажного дома на 1-м этаже вошли 5 человек. Вычислите вероятность того, что на 6-м этаже выйдут трое из них.
№ 12.В четырех опытах, проводимых по схеме Бернулли, вероятность хотя бы одного успеха равна 0,5904. Что более вероятно в этих четырех опытах: достижение ровно двух успехов или ровно трех успехов?
№ 13.Книга в 500 страниц содержит 400 опечаток. Предположим, что каждая из них независимо от остальных опечаток может с одинаковыми вероятностями оказаться на любой странице книги. Оценить вероятность того, что на 13-й странице будет не менее двух опечаток.
№ 14.Книга из 600 страниц содержит в среднем по одной опечатке на страницу. Оцените вероятность того, что на 13-й странице:
а) нет ни одной опечатки;
б) ровно две опечатки;
в) не более двух опечаток.
№ 15.Завод отправил на базу 10000 стандартных изделий. Среднее число изделий, поврежденных при транспортировке, составляет 0,02 %. Найти вероятность того, что из 10000 изделий: 1) будет повреждено: а) 3; б) по крайней мере 3; 2) не будет повреждено: а) 9997; б) хотя бы 9997.
№ 16.На сборку поступают детали из трех автоматов. Первый дает в среднем 0,2 % брака, второй – 0,1 % брака; продукция, поступающая с третьего автомата, не содержит бракованных изделий. На сборку поступило 2000 деталей с первого автомата, 3000 деталей со второго автомата и 5000 деталей с третьего автомата.
1) Найдите вероятность того, что деталь, выбранная наугад из всех деталей, будет бракованной.
2) Какова вероятность того, что деталь, выбранная наугад из данных деталей, поступила с первого автомата, если известно, что она является бракованной?
№ 17.В специализированную клинику поступают больные с одним из заболеваний А, В, С: в среднем 50 % больных с заболеванием А, 30 % с заболеванием В и 20 % с заболеванием С. Вероятности полного излечения этих болезней равны 0,95, 0,90 и 0,85 соответственно.
1) Какова вероятность того, что выбранный наугад пациент клиники будет вылечен полностью? 2) Больной, поступивший в клинику, был полностью вылечен. Какова вероятность того, что он страдал заболеванием В?
№ 18.Из первой урны, содержащей 8 белых и 4 черных шара, наугад переложили один шар во вторую урну, содержащую 2 белых и 3 черных шара. Затем из второй урны наугад извлекли один шар.
1) Какова вероятность того, что извлеченный из второй урны шар оказался белым? 2) Шар, извлеченный из второй урны, оказался белым. Вычислите вероятность того, что из первой урны во вторую был переложен белый шар.
№ 19.Из первой урны, содержащей 5 белых и 3 черных шара, наугад переложили два шара во вторую урну, содержащую 2 белых и 6 черных шаров. Затем из второй урны наугад извлекли один шар.
1) Какова вероятность того, что извлеченный из второй урны шар оказался белым? Шар, извлеченный из второй урны, оказался белым. Вычислите вероятность того, что из первой урны во вторую были переложены шары разного цвета.
№ 20.В рекламных целях торговая фирма вкладывает в каждую десятую единицу товара денежный приз размером 1 тыс. рублей. Составить закон распределения случайной величины – размера выигрыша при пяти сделанных покупках. Найти математическое ожидание и дисперсию этой случайной величины.
№ 21.Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок с вероятностью 0,1. Составить закон распределения числа возвращенных в срок кредитов из 5 выданных. Найти математическое ожидание и дисперсию этой случайной величины.
№ 22.Контрольная работа состоит из 3 вопросов. На каждый вопрос приведено 4 ответа, один из которых правильный. Составить закон распределения числа правильных ответов при простом угадывании. Найти математическое ожидание и дисперсию этой случайной величины.
№ 23. Функция распределения случайной величины Х имеет вид:
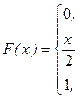
Найти плотность вероятности непрерывной случайной величины Х.
№ 24. Функция распределения случайной величины Х имеет вид:
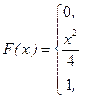
Найти плотность вероятности непрерывной случайной величины Х.
№ 25. Функция распределения случайной величины Х имеет вид:
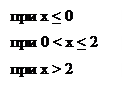
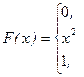
Найти плотность вероятности непрерывной случайной величины Х.
Приложение 6
Таблица
