Ортометрическая система высот

Эта система высот базируется на теории действительного потенциала силы тяжести.

B

h₃

h₂

h₁ В₀ геоид

РИС.10

Пусть для определения высоты точки В над точкой A выполнено нивелирование и определены превышения h₁,h₂,…, Разность потенциала между точками A и В равна

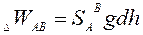(113)

Разность потенциалов между точками В и В₀ будет

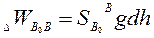(114)

Поскольку точки В₀ и A лежат на одной уровенной поверхности, то разность потенциалов между ними будет одинаковой, то есть

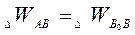(115)

Или

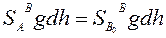(116)

Поскольку нас интересует значение высоты точки B относительно A по отвесной линии ВВ₀, то на основании теории о среднем, запишем

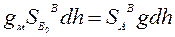(117)

Где g_м – среднее значение ускорения силы тяжести на отвесной линии ВВ₀ , или

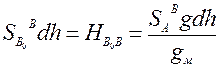(118)

Из этой формулы следует однозначное определение высоты точки В над точкой В₀ по отвесной линии. Проблема заключается в том, что практически неизвестным остаётся значение g_м. Для его определения следовало бы измерить значения g вдоль отвесной скважины ВВ₀ и найти из них среднее значение g_м, что практически невозможно.

Нормальная система высот.

Эта система строится на основе ортометрической. Только вместо неизвестного значения g_м в этой системе применяют γ_м , то есть, среднее значение нормальной силы тяжести на нормали ВВ₀ к эллипсоиду.

Здесь предлагается выполнение следующего равенства

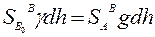(119)

Из которого следует

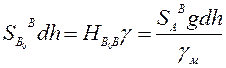(120)

Нормальная система высот неудобна в строительстве. Значение γ изменяется в зависимости от широты. Поэтому возможны, случаи, когда точки одной уровенной поверхности имеют различные нормальные высоты, что неудобно при строительстве. В таком случае используется динамическая система высот.

Динамическая система высот.

В этой системе высот вместо γ_м в формуле (120) используется некоторая постоянная величина. Например, значение ускорения силы тяжести на широте 45°, тогда динамическая высота точки В будет:

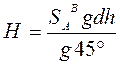(121)

Глава 5. Понятие о теории Молоденского определения

Фигуры Земли.

Согласно теории Стокса все измерения над уровенной поверхности геоида. Для определения высот геоида над эллипсоидом необходимо измеренное ускорение силы тяжести (силу тяжести) редуцировать на поверхность геоида. С теоритической точки зрения такое редуцирование возможно, но практически не осуществимо. Это вызвано тем, что для вычисления редукции за влияние масс Земли, возвышающихся над геоидом, необходимо знать их плотность, в каждой точке. К настоящему времени таких знаний даже в регулярной сети точек не накоплено. И плотность масс известно лишь приблизительно. Ясно, что для строгого определения высоты геоида над эллипсоидом такие приблизительные значения не подходят.

В связи с этим советский ученый Молоденский предложил определять их – высоту геоида над эллипсоидом. В этом случае в точке M земной поверхности измеряется сила тяжести g. Потенциал реальной силы тяжести в этой точке обозначается через W(B,L.H), где B,L.H геодезические широта, долгота и высота точки. Потенциал нормальной силы тяжести, создаваемой эллипсоидом в этой точке будет равен U(B,H). В нем отсутствует долгота, так как по формуле Сомильяни сила тяжести от долготы не зависит.

Запишем теперь формулу возмущенного потенциала:

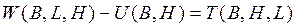(122)

Дифференцирование (122) по нормали к эллипсоиду приводит к выражению

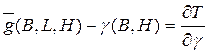(123)

M' x

h

H

M

M₀

РИС.11

В формуле (123) 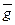является производной W по нормали к эллипсоиду. Поскольку измеряется производная по нормали к геоиду g, то зная уклонение отвесной линии U в точке H можно найти, что

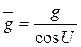(124)

Значение 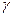в (123) найдем по формуле:

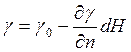(125)

где 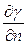производная силы тяжести по нормали в точке M₀.

С учетом (125) формулу (123), пологая, DH=H, можно переписать так:

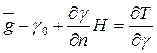(126)

В действительности H неизвестно. Вместо него по результатам нивелирования известна некоторая приближенная величина h.Так что можно записать:

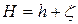(127)

При этом 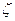не играет роль высота геоида над эллипсоидом. Это поправка L приближенной высоте h.

Для ее определения найдем сначала нормальный потенциал в точке M¢

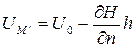(128)

где 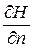берется в начальной точке M₀. Тогда значение U_м запишем так:

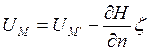(129)

где 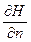берется в точке М¢.

Подставляя (129) в (122) запишем:

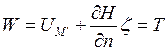(130)

И

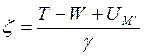(131)

где 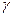- значение нормальной силы тяжести в точке М¢.

С учетом (128) выражение (131) можно записать еще и так:

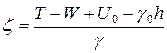(132)

В (132) реальный потенциал запишем так

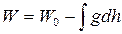(133)

В соответствии с теорией нормальных высот:

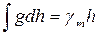(134)

где 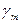-значение нормальной силы тяжести на глубине 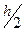от точки М.

Учитывая (134) и (133) выражение (132) перепишем в виде:

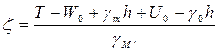(135)

или

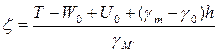(136)

В частном случае можно принять, что

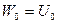(137)

и тогда

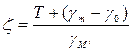(138)

Выражение (126) с учетом (130) примет вид:

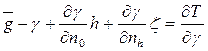(139)

Значение

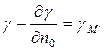(140)

является ускорением силы тяжести в точке М¢. С его учетом (139) перепишется так:

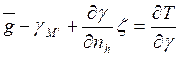(141)

Это дифференцированное уравнение является краевым условием Молоденского для определения возмущающего потенциала Т в точках земной поверхности. Принято считать его обобщением краевого условия Стокса.