Формулировка транспортной задачи

Экономическая и математическая формулировка транспортной задачи. Необходимое и достаточное условия ее разрешимости.

Формулировка транспортной задачи.

Однородный груз сосредоточен у m поставщиков в объемах 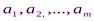. Данный груз необходимо доставить n потребителям в объемах 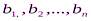. Известны 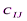, i=1,2,,…,m, j=1,2,…,n- стоимости перевозки единицы груза от каждого I-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок, при котором запасы всех потребителей полностью удовлетворены и суммарные затраты на перевозку всех грузов минимальны.

Исходные данные транспортной задачи обычно записываются в таблице (таб1.1).

			…
			…
			…
…	…	…	….	….
			…

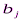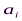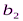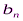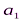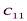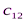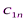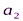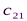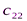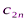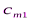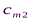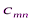Таблица1.1.

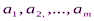Исходные данные задачи могут быть представлены также в виде вектора запасов поставщиков А=( ), вектора запросов потребителей

В =( 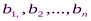) и матрицы стоимостей .

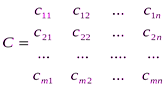В транспортных задачах под поставщиками и потребителями понимаются различные промышленные и сельскохозяйственные предприятия, заводы, фабрики, слады, магазины и т.д. Однородными считаются грузы, которые могут быть перевезены одним видом транспорта. Под стоимостью перевозок понимаются тарифы, расстояния, время, расход топлива и т.п.

^ 2. Математическая модель транспортной задачи.

Переменными (неизвестными) транспортной задачи являются 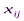i=1,2,,…,m, j=1,2,…,n – объемы перевозок от каждого i-го поставщика каждому j-му потребителю. Эти переменные можно записать в виде матрицы перевозок

.

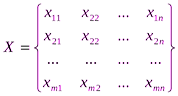Так как произведение 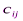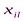определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны 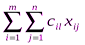. По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция имеет вид .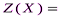

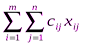
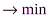Система ограничений задачи состоит из двух групп уравнений. Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью:

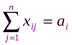, i=1,2,…,m.

Вторая группа из n уравнений выражает требование полностью удовлетворить запросы всех n потребителей:

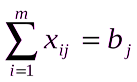, j=1, 2, … , n.

Учитывая условие неотрицательности объемов перевозок, математическую модель задачи можно записать так:

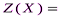
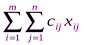
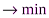, (1)

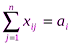, i=1,2,…,m , (2)

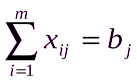, j=1, 2, … , n, (3)

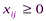, i=1,2,,…,m, j=1,2,…,n (4)

В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е. .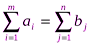

Такая задача называется задачей с правильным балансом,а ее модель – закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом,а ее модель – открытой.

Математическая формулировка транспортной задачи такова: найти переменные задачи 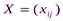, i=1,2,,…,m, j=1,2,…,n, удовлетворяющие системе ограничений (2), (3), условиям неотрицательности (4) и обеспечивающие минимум целевой функции (1).

Математическая модель транспортной задачи может быть записана в векторном виде.. Тогда математическая модель транспортной задачи запишется следующим образом:

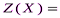
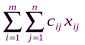
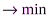, (7)

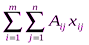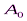= , (8)

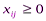, i=1,2,,…,m, j=1,2,…,n (9)