Схема повторных испытаний. Формула Бернулли и её асимптотика

Пусть в рамках некоторого опыта рассматривается событие А. Известна вероятность 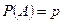появления А в данном опыте; вероятность противоположного события обычно обозначают 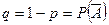. Пусть далее опыт повторяется n раз (или проводится n одинаковых опытов).

Основной задачей при этом является вычисление вероятности 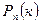- вероятности того, что в результате n опытов событие А появится ровно k раз. Эта вероятность вычисляется по знаменитой формуле Бернулли:

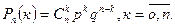(13)

Схема повторных испытаний и, следовательно, формула Бернулли имеют огромное применение в теории вероятностей.

Пример 24. Двое равносильных соперников соревнуются в игре, в которой ничьи не допускаются. Простейший пример – подбрасывание монеты. Выпал герб – выиграл 1-й игрок, выпала цифра – выиграл 2-й. Что вероятнее выиграть: две партии из четырёх или три партии из шести?

Решение. Поскольку соперники равносильны, то вероятности выигрыша у обоих равны р = ½. Следовательно, надо сравнить 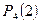и :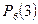

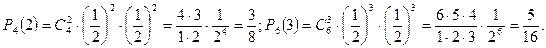
Итак,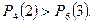

Заметим, что обычно на лекции преподаватель перед решением этой задачи спрашивает студентов, какой результат они ожидают (интуитивно), и в ответ, как правило, слышит все три возможных исхода. На самом деле объяснение полученного неравенства простое.

Таблица 1

k
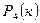	1/16	1/4	3/8	1/4	1/16	-	-
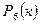	1/64	3/32	15/64	5/16	15/64	3/32	1/64

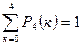
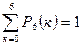
В таблице 1 приведены вычисления 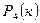и 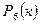для всех возможных k. Сумма вероятностей в каждой строке равна, естественно, единице. Но во второй строке единица распределена на пять частей, а в третьей – на семь, поэтому каждой части досталось меньше. В дальнейшем такое распределение вероятностей мы назовём биноминальным.

Пример 25. Сколько нужно взять случайных цифр, чтобы вероятность появления среди них цифры 5 была не меньше 0,9?

Решение. Можно задачу свести к схеме повторных испытаний. Поскольку цифр всего 10, то вероятность события А = (появление цифры 5) в одном опыте равна р=1/10. В серии из n опытов событие А может появиться 1,2,….n число раз и не появиться в одном случае, поэтому перейдём к противоположному утверждению, – вероятность не появления цифры 5 будет меньше 0,1, т.е. в формуле Бернулли 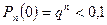. Поскольку

q =1-p=0,9, то решим неравенство 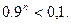Прологарифмируя, получим

n lg 0,9<lg0,1 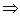n > 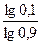(учли, что lg 0,9 < 0) 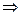n > 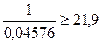. Итак, n .

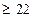Нетрудно видеть, что использование формулы Бернулли уже при n > 10 сопровождается громоздкими вычислениями. Поэтому возникает естественное желание иметь простые приближённые формулы для формулы Бернулли. Рассмотрим несколько таких формул.

Итак, событие А в одном опыте имеет вероятность 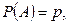1-р =q. Проводится n опытов и по формуле Бернулли вычисляется 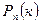- вероятность того, что в n опытах А появится ровно k раз.

Формула Пуассона. Если n-велико, а р-мало, но при этом 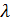= 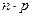также мал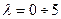о ( ), то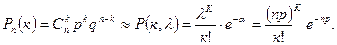

Эта формула называется формулой Пуассона.

Локальная формула Муавра-Лапласа.

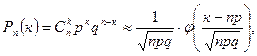
где 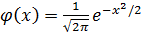- так называемая малая функция Лапласа; она чётная 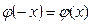, табулирована.

На примере 24 уже можно понять, что при больших n каждая из вероятностей 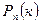весьма мала и их практическая ценность столь же мала, как и сама вероятность. Поэтому значение приобретают вероятности 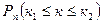- вероятность того, что число k появлений события А в n опытах окажется на отрезке 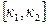. Приближённое вычисление таких вероятностей даёт интегральная формула Лапласа:

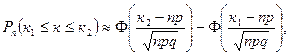где

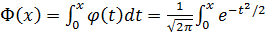- так называемая функция Лапласа, 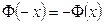, табулирована.

Отметим огромное значение приведенных формул. Пользоваться ими легко – для них составлены таблицы, которые имеются в каждом учебнике или задачнике по теории вероятностей.

О правомочности применения указанных формул скажем несколько позже, а пока рассмотрим примеры.

Пример 26. Проводится 10 одинаковых опытов. В каждом опыте вероятность события А равна 0,9. Вычислим 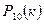, k = 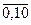по формуле Бернулли, по приближённым формулам Пуассона и локальной Муавра-Лапласа.

Предварительно учтём следующее замечание.

Формулу Пуассона ещё называют законом редких явлений – её применение тем точнее, чем меньше число 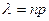или число .

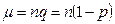В нашем примере 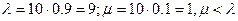, поэтому лучше использовать 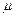. При этом руководствуемся следующими рассуждениями: вероятность 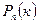того, что в результате n опытов событие А появится ровно k раз, равна вероятности того, что событие А не появится ровно (n-k) раз, т.е. событие 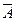появится ровно (n-k) раз.

Таким образом, вероятность 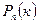можно с помощью формулы Пуассона вычислять двумя способами:

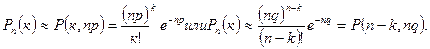
Предпочтение следует отдавать той формуле, в которой меньше параметр 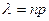или .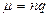

Например, по формуле Бернулли, 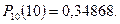По таблицам для формулы Пуассона 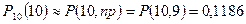; 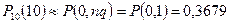. Как видим, вторая формула значительно точнее приближает истинное значение.

Применение локальной формулы Муавра-Лапласа вовсе не представляет труда – всё ограничивается арифметическими вычислениями и использованием таблиц. Например,

Теперь все вычисления 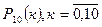сведём в таблицу 2.

Таблица 2.

k	Точное значение по формуле Бернулли	Приближение по формуле Пуассона	Приближение по формуле Муавра-Лапласа
		0,00001
	0,00001	0,00007
	0,00014	0,00051
	0,00149	0,00307	0,00006
	0,01116	0,01533	0,00286
	0,05740	0,06131	0,04540
	0,19371	0,18394	0,24231
	0,38742	0,36788	0,42052
	0,34868	0,36788	0,24231

Как видим, для данного примера формула Пуассона даёт лучшее приближение по сравнению с локальной формулой Муавра-Лапласа.Но так бывает не всегда.

Пример 27. Подбрасывается монета 10 раз. Вероятность выпадения герба в одном опыте p = 0,5, q = 0,5, np =nq = 5. Вычислим 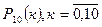по всем трём формулам и сравним (табл.3)

Таблица 3.

k	Точное значение по формуле Бернулли	Приближение по формуле Пуассона	Приближение по формуле Муавра-Лапласа
	0,00098	0,00674	0,00171
	0,00977	0,03369	0,01028
	0,04395	0,08422	0,04150
	0,11719	0,14037	0,11408
	0,20508	0,17547	0,20690
	0,24609	0,17547	0,25231
	0,20508	0,14622	0,20690
	0,11719	0,10444	0,11408
	0,04395	0,06528	0,04150
	0,00977	0,03627	0,01028
	0,00098	0,01813	0,00171

Как видим, в этом примере применение локальной формулы Муавра-Лапласа предпочтительнее.

Два последние примера показывают нам, что даже при n = 10, когда ещё и формулой Бернулли пользоваться не обременительно, приближённые формулы дают неплохие результаты. Если же n велико, то формулы дают ещё лучшие результаты. С другой стороны, как уже отмечалось, каждая из вероятностей 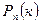мала. Лишь некоторые из них имеют практическое значение, они так и называются – наивероятнейшее число появлений события А в n опытах. (см.табл.2 и 3). Поэтому больший практический интерес представляет вычисление вероятности попадания числа появлений события А на некоторый отрезок.

Например, вычислим для примера 27 (табл.3) 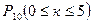и 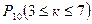. Во-первых, воспользуемся данными табл. 3 (складывая соответствующие вероятности).

1) По формуле Бернулли:

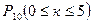= 0,00098+0,00977+0,04395+0,11719+0,20508+0,24609=0,62306.

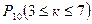= 0,11719+0,20508+0,24609+0,20508+0,11719=0,89063.

2) По формуле Пуассона:

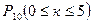=0,61596; 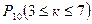=0,74197

3) По локальной формуле Муавра-Лапласа:

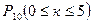=0,62678; 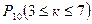= 0,89437.

Воспользуемся для вычисления указанных вероятностей интегральной (её ещё называют интервальной) формулой Лапласа:

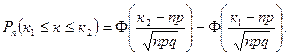
В нашем примере n =10, p =q = 0,5, следовательно, np = 5, npq = 2,5, 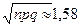.Таким образом, 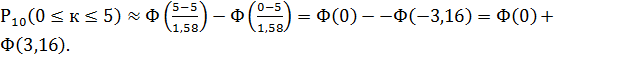По таблицам функции Лапласа находим: 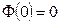, 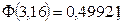следовательно,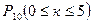 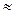0,499.

Аналогично,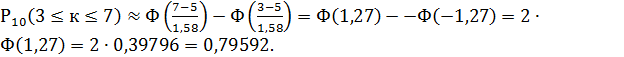

Конечно, интегральная формула Лапласа эффективна при больших n.

Пример 28. По каналу связи передано 100 сигналов. Вероятность искажения сигнала равна 0,1. Действие помех на каждый сигнал происходит независимо. Какова вероятность того, что при передаче будет не более 10 искажений?

Решение. Эта задача – на схему повторных испытаний, n = 100, p = 0,1, q = 0,9, np = 10, npq = 9, 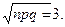. Легко понять, что использование всех формул весьма громоздко, за исключением интегральной формулы Лапласа: