Принципы решения хорошо структурированных проблем
Классификация проблем по степени их структуризации.
Саймон Ньюэлл предлож. Все П делить на 3 класса по степени их структуризации.
1. Хорошо структурированные - хорошо формализ., колич.опис.
2. Слабо структурированные – колич. И кач. опис.
3. Неструктурированные – неформализ., кач. опис.
В каждой проблеме можно выделить:
1. Цель
2. Альтернативы AL
3. Ресурсы R
4. Модели для оценки AL
5. Критерии выбора лучш. AL
Цель – желаемое состояние динамики процесса.
AL – способы достижения цели.
Критерий – признак или правило сравнения AL и выбор лучший.
1.2 – Классификация задач и мет. ИО
ИО: реш-ся проблемы с хорошо структурир. реш. след. задачи:
1. План снабжения предприятий
2. Планирование внедр. в пр-во
3. Продажа изонных товаров
4. Военные опер.
Операция – управляем. мероприят. По достиж. Опред. Цели.
Все эти зад. Им. Общее:
1. Все зад. Развернуты во времени
2. Все услов. реш. дел-ся на гр: зависящие от нас и независящие
3. Необх. Принять оптим. решение
Принципы формализации эвристической информации
Полученную от экспертов эвристическую информацию необходимо представить в качественной форме, которая удобна для обработки и анализа. При этом для формализации эвристической информации служат следующие типы шкал:
1. шкала классификаций, позволяющая изучать исследуемые объекты с помощью тех или иных чисел; 2. шкала порядка, позволяющая упорядочить исследуемые объекты по какому-либо признаку; 3. шкала интервалов, позволяющая приписать исследуемым объектам относительные числовые значения; 4. шкала отношений, позволяющая приписать исследуемым объектам абсолютные числовые значения;
Приведем пример шкал для формализации эвристической информации:
Лингвистические оценки Бальные оценки Шкала Харрингтона
Отлично 5 0,8-1
Хорошо 4 0,63-0,8
Удовлетворительно 3 0,37-0,63
Плохо 2 0,2-0,37
Очень плохо 1 0-0,2
Шкала Харрингтона имеет аналитической описание в виде функции полезности: y = exp[-exp(-x)], 0≤y≤1, где х — исследуемая величина в диапазоне [-6;6]. С помощью шкалы Харрингтона можно привести векторные оценки с различной размерностью к безразмерному виду.
Принципы решения хорошо структурированных проблем
Для решения проблем этого класса широко используются математические методы И.О. В операционном исследовании можно выделить основные этапы:
1. Определение конкурирующих стратегий достижения цели. 2. Построение математической модели операции. 3. Оценка эффективностей конкурирующих стратегий. 4. Выбор оптимальной стратегии достижения целей. Математическая модель операции представляет собой функционал E = f(x∈x^, {α}, {β})⇒ extz
Е - критерий эффективности операций; x - стратегия оперирующей стороны;
a - множество условий проведения операций; b - множество условий внешней среды. Модель позволяет оценить эффективность конкурирующих стратегий и выбрать из их числа оптимальную стратегию.
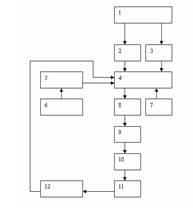
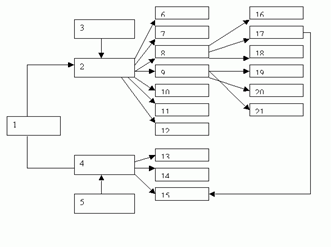
Рис. 22.1 — Выбор оптимальной Рис. 22.2 — Требования к критерию
стратегии достижения целей эффективности исследования операций
1. постоянство проблемы 2. Ограничения 3. критерий эффективности операций 4. математическая модель операции 5. параметры модели, но часть параметров, как правило, не известна, поэтому (6) 6. прогнозирование информации (т.е. нужно предугадать ряд параметров) 7. конкурирующие стратегии 8. анализ и стратегии 9. оптимальная стратегия 10. утвержденная стратегия (более простая, но которая удовлетворяет еще ряду критериев) 11. реализация решения 12. корректировка модели
Критерий эффективности операции должен удовлетворять ряду требований:
1. Представительность, т.е. критерий должен отражать основную, а не второстепенную цель операции.
2. Критичность — т.е. критерий должен изменяться при изменении параметров операций.
3. Единственность, так как только в этом случае возможно найти строгое математическое решение задачи оптимизации.
4. Учет стохастичности, которая связана обычно со случайным характером некоторых параметров операций.
5. Учет неопределенностей, которая связана с отсутствием какой-либо информации о некоторых параметров операций.
6. Учет противодействия, которое вызывает часто сознательный противник, управляющий полными параметрами операций.
7. Простая, т.к. простой критерий позволяет упростить математические выкладки при поиске opt. решения.
Приведем схему, которая иллюстрирует основные требования к критерию эффективности исследования операций.
1. постановка проблемы (вытекают 2 и 4 (ограничения));
2. критерий эффективности;
3. задачи верхнего уровня
4. ограничения (мы организуем вложенность моделей);
5. связь с моделями верхнего уровня;
6. представительность;
7. критичность;
8. единственность;
9. учет стохастичности;
10. учет неопределенности;
11. учет противодействия (теория игр);
12. простота;
13. обязательные ограничения;
14. дополнительные ограничения;
15. искусственные ограничения;
16. выбор главного критерия;
17. перевод ограничений;
18. построение обобщенного критерия;
19. оценка математического ожид-я;
20. построение доверительных интервалов:
21. анализ возможных вариантов (есть система; мы точно не знаем, какова интенсивность вх. потока; мы можем только с определенной вероятностью предположить ту или иную интенсивность; затем взвешиваем выходящие варианты ).
