Теоретические сведения. Критерий устойчивости Найквиста изначально сформулирован для АФХ WР(jw)

Критерий устойчивости Найквиста изначально сформулирован для АФХ WР(jw). На комплексной плоскости фиксируется так называемая критическая точка с координатами (-1, j0) – см. рис. 14.1.

При изменении частоты w от 0 до µ, прохождение годографа WР(jw) через отрицательную часть оси мнимых означает, что точке пересечения годографа с осью соответствует фазовый сдвиг –p. Частота на АФХ в точке пересечения обозначается “wp”.

Критерий Найквиста определяет устойчивость по соотношению положения точки пересечения WР(jwp) и критической точки (-1, j0).

Если точка АФХ WР(jwp) находится слева от точки (-1, j0), то говорят, что АФХ “охватила” критическую точку. При этом имеем модуль АФХ RР(wp) > 1.

Если точка АФХ WР(jwp) находтся справа от точки (-1, j0), то говорят, что АФХ “не охватила” критическую точку. При этом имеем модуль АФХ RР(wp) < 1.

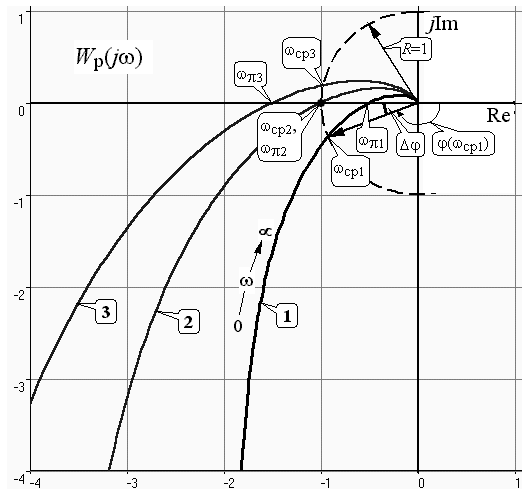
Рис. 14.1

Теперь можем сформулировать простые правила критерия Найквиста.

- Если при изменении частоты w от 0 до µ АФХ WР(jw) не охватывает критическую точку, то замкнутая система устойчива.

- Если при изменении частоты w от 0 до µ АФХ WР(jw) охватывает критическую точку, то замкнутая система неустойчива.

- Если при изменении частоты w от 0 до µ АФХ WР(jw) проходит через критическую точку, то замкнутая система находится на колебательной границе устойчивости.

На рис. 14.1. изображена комплексная плоскость, на которой построена полуокружность единичного радиуса и помечена точка (-1, j0).

Построены АФХ для той же СУ, устойчивость которой исследовалась алгебраическим критерием

Кривая “1” соответствует значению коэффициента усиления K = 1< Kкр. Действительно, в этом случае АФХ WР(jw) не охватила критическую точку, то есть замкнутая система устойчива

Кривая “2” построена при значении коэффициента усиления K = 2 = Kкр. В этом случае АФХ WР(jw) прошла через критическую точку и замкнутая система находится на колебательной границе устойчивости

Кривая “3” соответствует значению коэффициента усиления K = 3 > Kкр. В этом случае АФХ WР(jw) охватила критическую точку, то есть замкнутая система неустойчива

Точка пересечения АФХ WР(jw) с окружностью единичного радиуса (то есть единичного модуля ЧХ) соответствует частоте wср. Поэтому можно дать другую формулировку частотному критерию (см. рис. 14.1):

- при wср < wp система устойчива;

- при wср > wp система неустойчива;

- при wср = wp система находится на границе устойчивости.

Для устойчивых СУ с использованием критерия Найквиста вводятся количественные оценки “запасов” устойчивости. Наиболее распространенная оценка – запас по фазе Dj. Под ним понимают значение угла, на который следует “довернуть” вектор R(wср) до значения -p (см. рис. 14.1). Для “хороших” СУ с переходным процессом, имеющим перерегулирование s < 15%, должно выполняться Dj > (55¸60^о).

Применение критерия Найквиста для ЛЧХ

Построим ЛЧХ для рассмотренного выше примера СУ - рис. 14.2.

В данном случае удобнее пользоваться второй формулировкой критерия Найквиста.

Для кривой “1” имеет место wср < wp и система устойчива. При этом на рисунке показан запас по фазе Dj.

Также видно, что кривой “3” соответствует wср > wp и система неустойчива.

При при wср = wp имеем кривую “2” и систему на границе устойчивости.

Можно дать формулировку критерия для ЛЧХ:

- если LР(wp) < 0, то система устойчива;

- если LР(wp) > 0, то система неустойчива;

- если LР(wp) = 0, то система на границе устойчивости.

Критерий устойчивости Найквиста при использовании ЛЧХ позволяет легко определить критический коэффициент усиления для СУ высокого порядка. Действительно, при вариациях усиления в контуре, ФЧХ остается неизменной, а ЛАХ смещается параллельно самой себе вверх (при увеличении усиления) или вниз (при уменьшении усиления). Необходимо расположить ЛАХ таким образом, чтобы выполнилось wср = wp или, что то же самое, LР(wp) = 0. После фиксации ЛАХ по ее низкочастотному участку определяется коэффициент усиления в контуре.

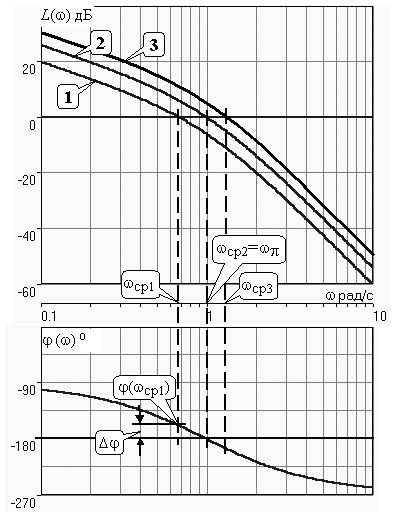
Рисунок 14.2

Оценка запасов устойчивости по ЛЧХ (рисунок 14.3).

Запас устойчивости по амплитуде A_m равен отклонению ЛАЧХ от нуля в сторону отрицательных значений на ближайших к часто­те среза w_ср частотах пересечения ЛФЧХ с линией минус 180°.

Запас устойчивости по фазе j_m равен отклонению ЛФЧХ на частоте среза w_ср от линии минус 180° в сторону положительных значений.

Как обычно, прежде всего сле­дует оценить, устойчива ли вообще данная система, только затем перехо­дить к определению запасов устойчи­вости. Из графика видно, что у систем со сложной формой ЛАЧХ (АФЧХ) могут существовать два запаса устой­чивости по амплитуде – запас на уве­личение коэффициента усиления A_m> и запас на уменьшение коэффициента усиления A_m<.

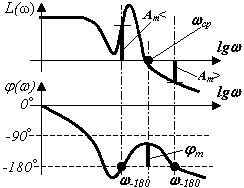
Рисунок 14.3

Напомним, что при увеличении коэффициента усиления ЛАЧХ смещается параллельно самой себе вверх, а при уменьшении – вниз.

Нормы запасов устойчивости, рекомендуемые при проектирова­нии: A_m = |DL(w)| = 20|lgA(ω_-π)| ³ 6…12 дБ; j_m ³ 30…60°.

В том случае, когда годограф W(jω) не имеет точек пересечения с вещественной осью слева от точки с коор­динатами (-1, j0), для устойчивости замкнутой сис­темы необходимо и достаточно, чтобы выполнялось условие

ω_с < ω_кр (14.1)

По L(ω) и φ(ω) разомкнутой системы можно определить за­пасы устойчивости: запас по фазе Δφ отсчитывают по фазо-частотной характеристике на частоте среза ω_с, а запас устойчивости по усилению ΔL равен зна­чению ЛАХ на критической частоте ω_кр, взятому с обратным знаком, т.е. ΔL = |L(ω_кр)| (см. рис. 14.4).

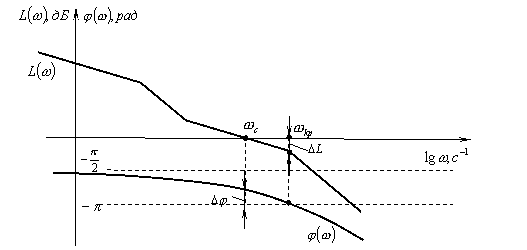
Рисунок 14.4 ЛАХ и ФЧХ устойчивой разомкнутой системы

Если при некотором значении коэффициента усиления (k) замкнутая система устойчива с запасом устойчивости по усилению равным ΔL, то величина критического коэффициента усиления k_кр может быть вычислена по формуле:

20lg k_кр = 20lg k + ΔL.

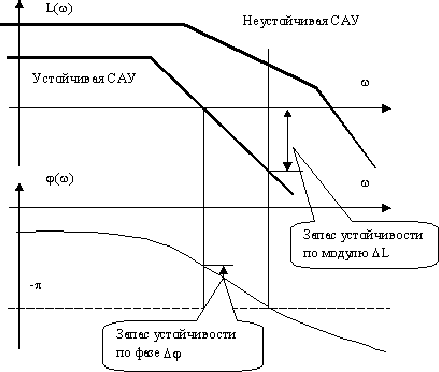
Рисунок. 14.5. ЛФЧХ устойчивой и неустойчивой САУ

Критическим значением коэффициента преобразования называется такое его значение, при котором АФЧХ проходит через точку (-1, j0) и система находится на границе устойчивости.

Запасом по модулю называется величина в децибеллах, на которую нужно изменить коэффициент преобразования САУ, чтобы привести ее к границе устойчивости.

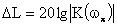, (14.2)

где 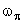— частота, при которой фазовая характеристика равна .

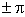Запасом устойчивости по фазе (рисунок 14.5) называется угол, на который нужно повернуть амплитудно-фазовую характеристику разомкнутой системы, чтобы замкнутая САУ оказалась на границе устойчивости.

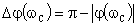, (14.3)

где 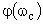– значение ФЧХ на частоте среза системы, для которой выполняется условие .

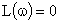Логарифмические частотные характеристики имеют большое практическое значение. Поэтому рассмотрим их построение. Часто результирующую передаточную функцию смешанного соединения звеньев можно свести к виду

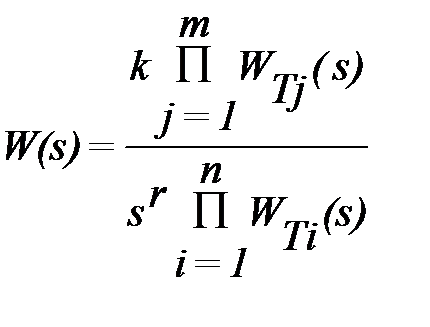, (14.4)

где W_T(s) - передаточная функция типового звена.

В этом случае построение ЛАХ производится по выражению

L(w) = 20lgA(w) = 20lg|W(jw)|=

= 20lgk - r´20lgw + - .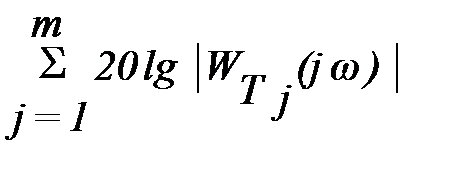

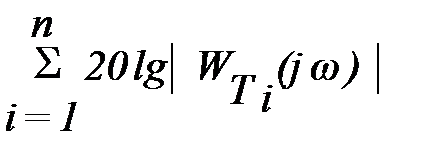Построение ЛФХ производится по выражению

y(w) = argW(jw) = -r´90⁰ + - .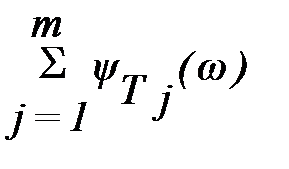

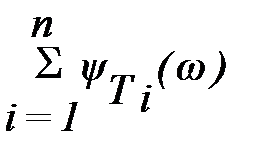Таким образом, результирующая ЛАХ определяется суммированием ЛАХ составляющих типовых звеньев, а результирующая ЛФХ - соответственно суммированием ЛФХ составляющих типовых звеньев. Таблицы характеристик типовых звеньев имеются в литературе.

Асимптотические ЛАХ можно построить непосредственно по виду передаточной функции по следующему правилу, состоящему из четырех пунктов.

1. Частотная область разбивается на диапазоны, границы которых определяются сопрягающими частотами, соответствующими постоянным времени передаточной функции:

.

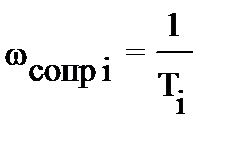Число сопрягающих частот равняется числу постоянных времени в передаточной функции, а число частотных диапазонов на единицу больше.

2. Первая низкочастотная асимптота ЛАХ, которая проводится в крайнем левом низкочастотном диапазоне, имеет наклон -(20´r)дб/дек и проходит через точку с координатами: w=1 с^{-1, L(1)=20lg k дб, где r - показатель степени оператора Лапласа s, записанного в знаменателе передаточной функции.}

3. На сопрягающих частотах ЛАХ претерпевает изломы.

3.1. Если сопрягающая частота соответствует постоянной времени Т_i, находящейся в знаменателе передаточной функции, то ЛАХ делает излом вниз на -(20´v)дб/дек, где v - порядок типового динамического звена, в которое входит эта постоянная времени Т_i.

3.2. Если сопрягающая частота соответствует постоянной времени Т_i, находящейся в числителе передаточной функции, то ЛАХ делает излом вверх на +(20´v) дб/дек, где v - порядок типового динамического звена, в которое входит эта постоянная времени Т_i.

4. Вторая асимптота проводится до следующей сопрягающей частоты и так далее.

Пример1. Построить логарифмические амплитудную и фазовую частотные характеристики разомкнутой линейной системы с передаточной функцией

при K = 500; Т1= 0,05с; Т2= 0,017с; Т3= 0,0025с; Т4= 0,001с.

Решение

Предварительно заполните таблицу, подобрав к каждому алгоритму конкретное соответствие из данного задания.

№ п/п	Алгоритм	Конкретное соответствие данной ситуации предложенному алгоритму
	Представить передаточную функцию САУ в частотном виде.	Частотная передаточная функция САУ имеет вид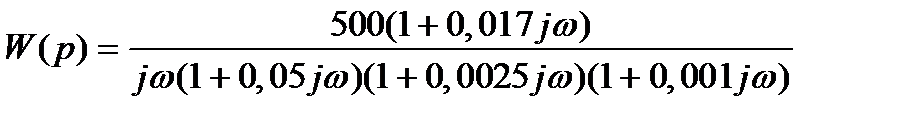
	Определить ординату ЛАЧХ на частоте w = 1 и значения асимптотических частот.	При w = 1ордината результирующей ЛАЧХ равна 20 lg K = 54. Значения асимптотических частот равны: w1 =1/T1 = 20(1/c), w2 = 1/T2 = 59(1/c), w3 = 1/T3 = 400(1/c), w4 = 1/T4 = 1000(1/c).
	Построить асимптотическую ЛАЧХ в соответствии с правилами.	Передаточная функция содержит одно интегрирующее звено, поэтому первую асимптоту проводим с наклоном –20 дБ/дек через точку с координатами (w = 1, L = 54) до ординаты на частоте w1 = 20(1/c). Здесь асимптотическая ЛАЧХ меняет наклон еще на –20 дБ/дек и с наклоном –40 дБ/дек идет до ординаты на частоте w2 = 59(1/c). Здесь асимптотическая ЛАЧХ меняет наклон на +20 дБ/дек и с наклоном –20 дБ/дек идет до ординаты на частоте w3 = 400 (1/c). Здесь асимптотическая ЛАЧХ меняет наклон на –20 дБ/дек и с наклоном –40 дБ/дек идет до ординаты на частоте w4 = 1000 (1/c), после которой она с наклоном –60 дБ/дек идет до –¥.

№ п/п	Алгоритм	Конкретное соответствие данной ситуации предложенному алгоритму
	Уточнить ЛАЧХ с учетом поправок.	К асимптотической ЛАЧХ прибавляем поправки для каждого элементарного звена (значения поправок приводятся в справочниках и определяются по специальным номограммам или таблицам*). Эти поправки для апериодических звеньев и дифференцирующего звена первого порядка одинаковы, но только разных знаков, и на асимптотической частоте имеют значение по модулю равное 3 дБ/дек.
	Пос­троить ЛФЧХ	Фазовая частотная характеристика системы определяется выражением 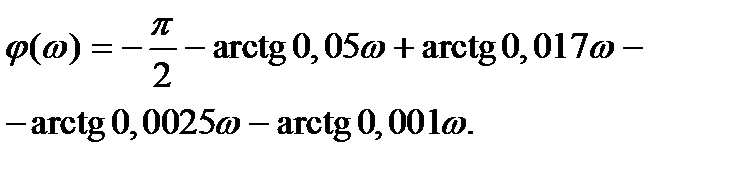ЛФЧХ определяем как сумму ординат фазовой частотной характеристики интегрирующего звена, трех апериодических звеньев и дифференцирующего звена первого порядка (фазовые характеристики элементарных звеньев имеют стандартный вид и имеются в справочниках в виде номограмм или таблиц).

Пример 2 .Рассмотрим вопрос определения запаса устойчивости по амплитуде и фазе дистанционной следящей системы, передаточная функция, которой в разомкнутом состоянии имеет вид:

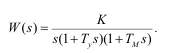
Для решения этой задачи необходимо построить на одном графике асимптотическую логарифмическую амплитудно-частотную характеристику и фазово-частотную характеристику следящей системы. Для построения этих характеристик необходимо вначале определить амплитудно-частотную характеристику системы. Для этого определим вначале частотную передаточную функцию, путем формальной замены 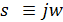. Выражение частотной передаточной функции получено в виде

(14.5)

На основе выделения вещественной и мнимой частей можно получить выражение для амплитудной частотной характеристики A(w), которое имеет вид (14.6).

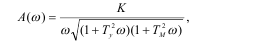(14.6)

Зная A(w) можно получить логарифмическую амплитудную частотную характеристику(ЛАЧХ) 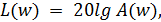то есть

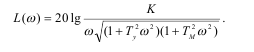
Отсюда,

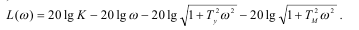(14.7)

Выражение для логарифмической фазовой частотной характеристики (ЛФЧХ) φ(w) имеет вид (14.8).

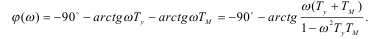(14.8)

На основании (14.7) и (14.8) построим на одном графике асимптотическую ЛАЧХ и ЛФЧХ (рисунок 14.6).

Для построения асимптотической ЛАЧХ необходимо нанести по оси частот ω логарифмический отсчет частот, по декадам. Одна декада пропорциональна десятикратному изменению частоты то есть 10ⁿ , где n - номер декады. Частоте 10⁰ =1 соответствует первая декада, на этой частоте откладываем по оси L(w) значение 20lg K . В результате получим точку а, от этой точки проводим прямую с наклоном – 20 дб/ дек , до первой сопрягающей частоты, которая определяется, например выражением 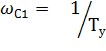. В результате получим точку б, от которой увеличиваем излом прямой и проводим её с наклоном - 40дб/ дек .

Вычисляем значение второй сопрягающей частоты 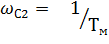, в результате получим точку в. От этой точки увеличиваем излом до -60 дб/дек. Таким образом, построим асимптотическую ЛАЧХ рассматриваемой системы (рисунок 14.6).

Далее построим ЛФЧХ, как видно их (14.8) эта характеристика начинается с -90^o на оси φ(ω) . Далее ЛФЧХ продолжается до величины угла - 270^o .

Для определения запаса по амплитуде, необходимо определить линию пересечения ЛФЧХ φ(ω) с частотой -180^o, точка ж. От этой точки проводим вверх прямую до пересечения с осью частот ω ЛАЧХ L(w) . Расстояние от точки д до оси частот ω определяет величину запаса по амплитуде, которая измеряется в децибелах.

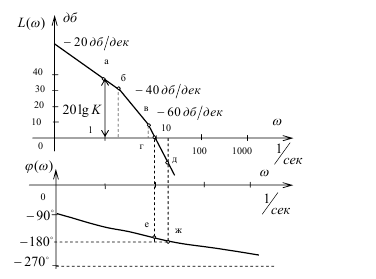
Рисунок 14.6 – Асимптотическая ЛАЧХ и ЛФЧХ дистанционной следящей системы

Для определения запаса по фазе, необходимо определить линию пересечения ЛАЧХ L(w) с осью частот ω, точка г. Далее от этой точки проводим прямую линию вниз до пересечения её с ЛФЧХ φ(ω) , точка е.

Расстояние от этой точки е до прямой отложенной на расстоянии -180^o соответствует величине запаса по фазе. Запас по фазе измеряется в градусах.

Задания:

Задача

- построение ЛАЧХ системы ;

- построение ЛФЧХ системы;

- определение устойчивости линейной системы по логарифмическим частотным характеристикам;

-по логарифмическим частотным характеристикам разомкнутой системы определелить запасы устойчивости системы по амплитуде и фазе.

Структурные схемы системы и параметры для различных вариантов приведены на рис. 14.7 – 14.21.

Схема № 1.

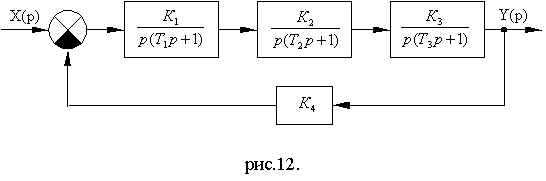
Рис. 14.7

Вариант № 0	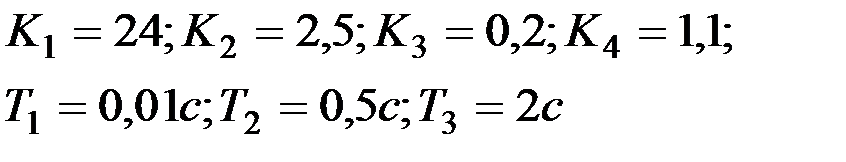Вариант № 1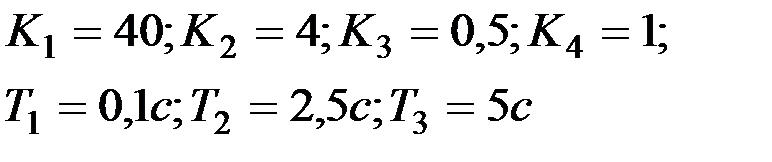
Вариант № 10	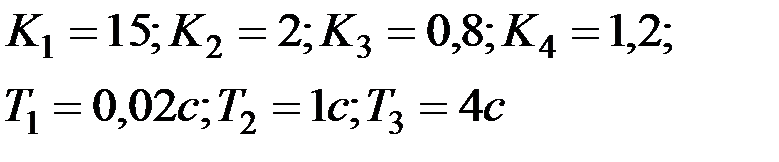Вариант № 11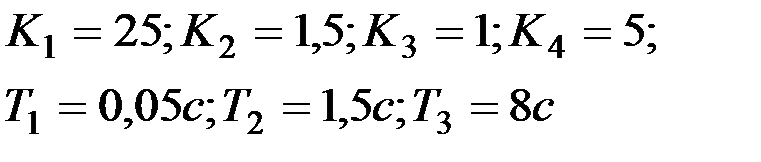
Вариант № 12	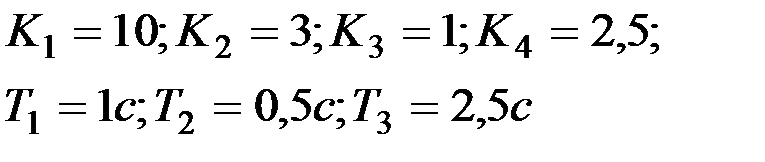Вариант № 13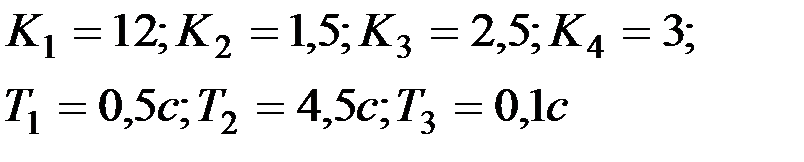
Вариант № 14	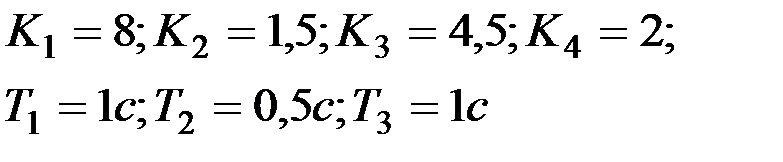Вариант № 15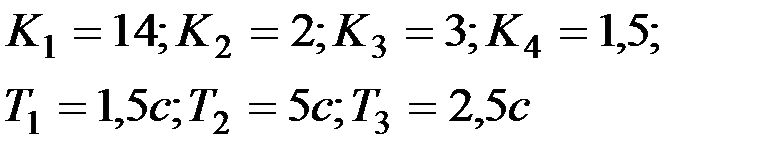

Схема № 2.

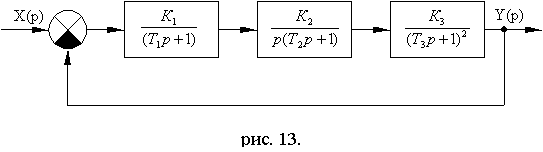
Рис. 14.8

Вариант № 2	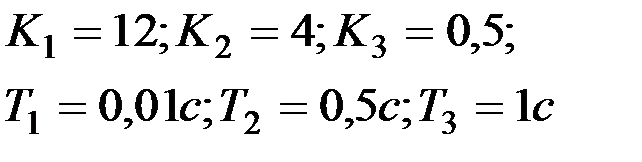Вариант № 3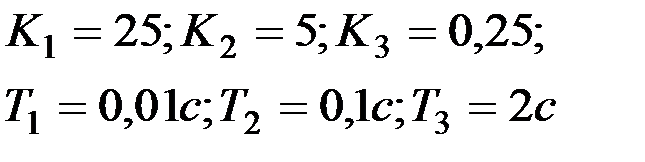
Вариант № 16	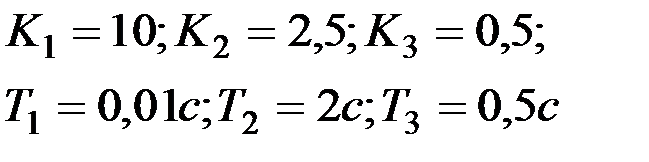Вариант № 17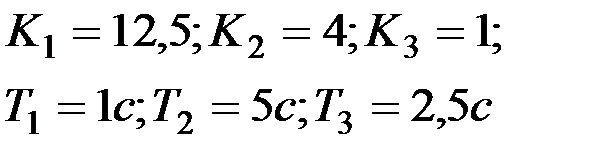
Вариант № 18	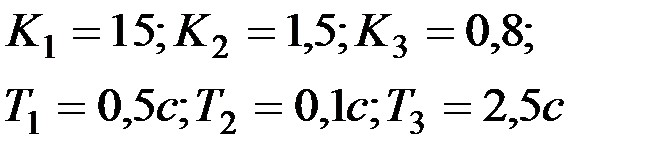Вариант № 19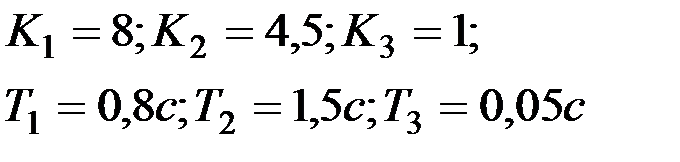
Вариант № 20	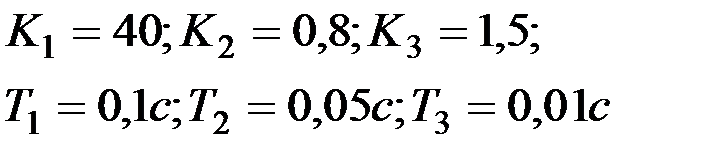Вариант № 21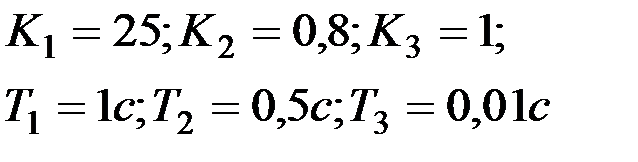

Схема № 3

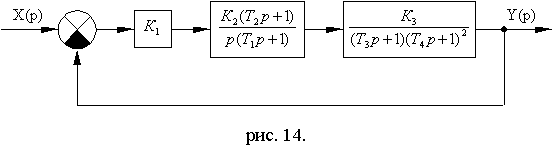
Рис. 14.9

Вариант № 4	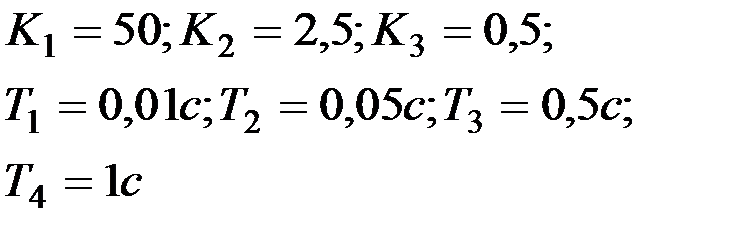Вариант № 5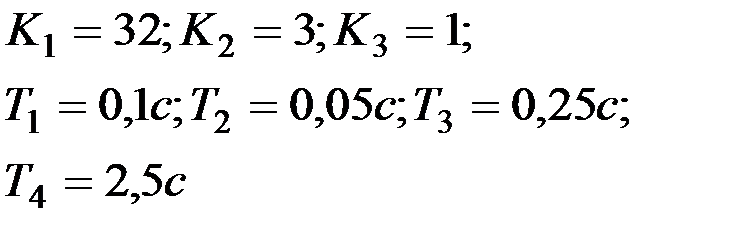
Вариант № 22	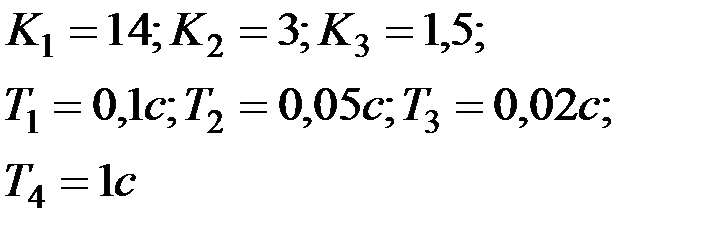Вариант № 23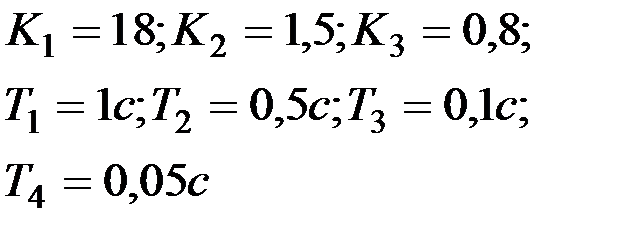
Вариант № 24	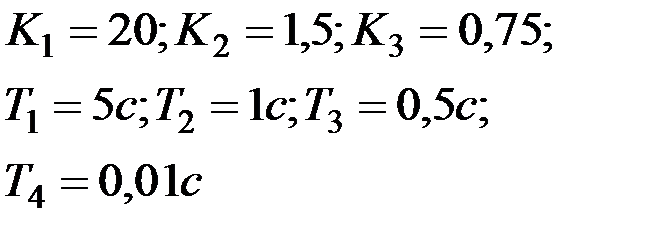Вариант № 25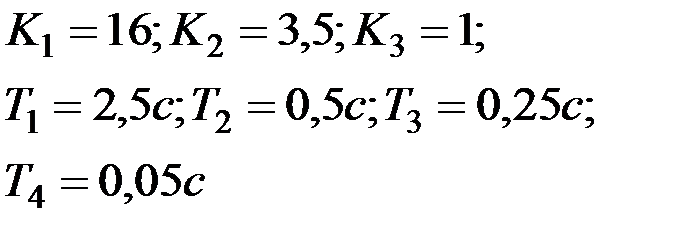

Схема№ 4

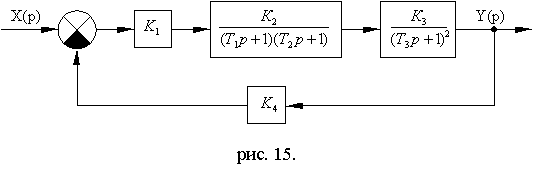
Рис. 14.10

Вариант № 6	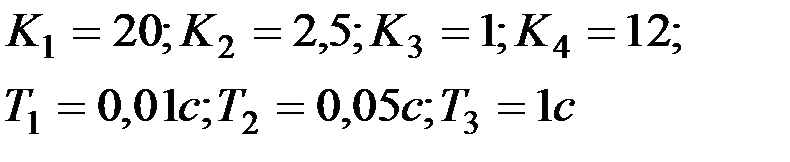Вариант № 7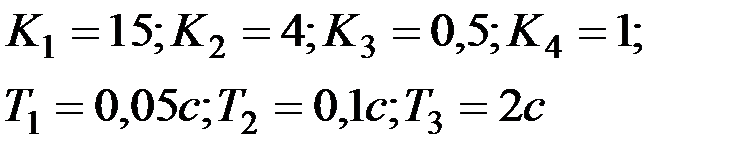
Вариант № 26	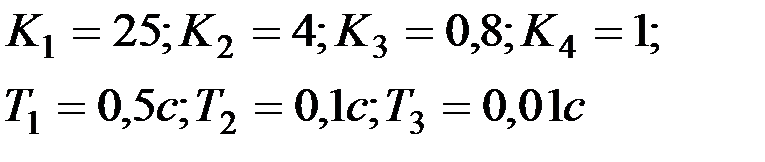Вариант № 27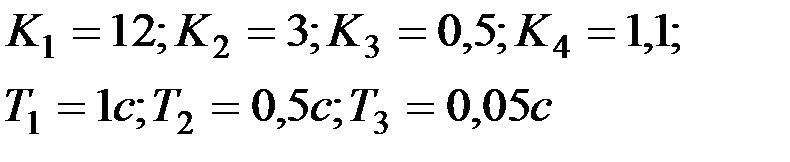

Схема № 5

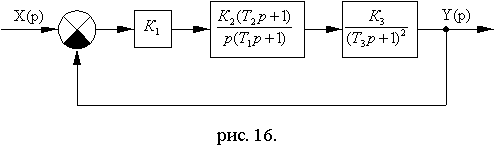
Рис. 14.11

Вариант № 8	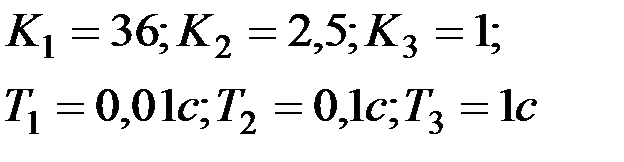Вариант № 9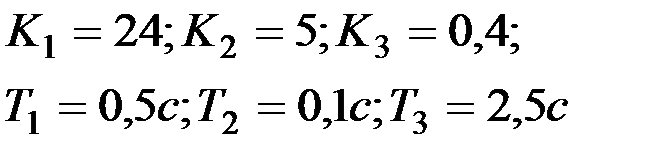
Вариант № 28	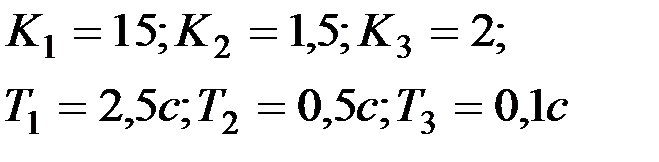Вариант № 29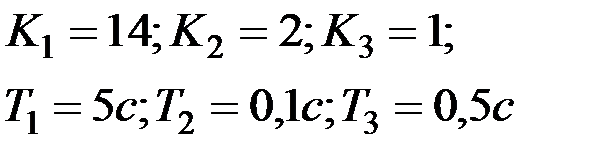

Литература: 1осн. [161-165], 7осн. [103-107].

Контрольные вопросы.

1) Как строится график асимптотической ЛАЧХ?

2) Как строится график ЛФЧХ?

3) Как определяется устойчивость системы по логарифмическим

характеристикам?

4) Как определяются запасы устойчивости по графику ЛАЧХ и ЛФЧХ?

Практическая работа № 15

Определение прямых и косвенных оценок качества регулирования
линейной системой.