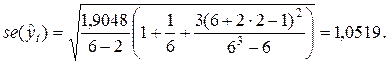Указания к выполнению контрольных заданий 2 страница
Парный коэффициент корреляции - это линейный коэффициент корреляции, характеризующий степень тесноты линейной связи между результативным и факторным признаками. Методика его расчета и интерпретация была изложена в пункте 3 задачи 1. При выполнении задания необходимо выписать матрицу парных коэффициентов корреляции и сделать выводы о наличии (отсутствии) в построенной модели мультиколлинеарности факторов.
Значения линейных коэффициентов парной корреляции представлены в матрице парных коэффициентов (таблица 3). Они определяют тесноту парных зависимостей между анализируемыми переменными.
Таблица 3.Парные коэффициенты линейной корреляции Пирсона
 |  |  | |
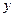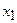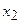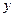| | 1,0000 (0,0) | 0,9393 (0,0001) | 0,4167 (0,2310) |
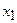| | 0,9393 (0,0001) | 1,0000 (0,0) | 0,4174 (0,2301) |
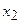| | 0,4167 (0,2310) | 0,4174 (0,2301) | 1,0000 (0,0) |
В скобках: P (  |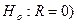
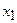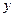Коэффициент корреляции между и свидетельствует о значительной и статистически существенной линейной связи между объемом продаж моющего средства и расходами на радио и теле рекламу. Увеличение расходов на рекламу поднимает объем продаж. Связь между 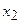и 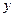не является статистически значимой. Кроме того, степень тесноты связи между 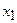и 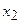выше, чем между 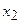и 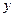. Таким образом, можно сделать предварительное заключение, что расходы на демонстрацию моющего средства в магазинах, существенно не влияют на рост объема продаж нового моющего средства.
Частные коэффициенты корреляции характеризуют тесноту связи между результативным и факторным признаками при фиксированном воздействии других факторов, включенных в уравнение регрессии. Их можно определить, используя парные коэффициенты корреляции по следующим рабочим формулам:
,
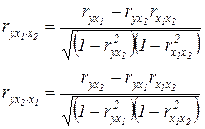где
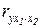- частный коэффициент корреляции между результативным и первым факторным признаками при фиксированном воздействии второго факторного признака,
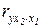- частный коэффициент корреляции между результативным и вторым факторным признаками при фиксированном воздействии первого факторного признака,
, 
, 
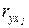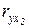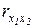- парные коэффициенты корреляции.
Интерпретируйте полученные значения частных коэффициентов корреляции и поясните причины различий между значениями частных и парных коэффициентов корреляции.
Приведенные в таблице 4 линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии.
Таблица 4. Коэффициенты частной корреляции
| | | | |
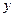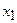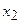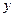| | 1,0000 (0,0) | 0,9265 (0,0003) | 0,0790 (0,8399) |
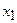| | 0,9265 (0,0003) | 1,0000 (0,0) | 0,0834 (0,8311) |
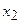| | 0,0790 (0,8399) | 0,0834 (0,8311) | 1,0000 (0,0) |
| В скобках: P ( |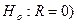
Коэффициенты частной корреляции дают более точную характеристику тесноты зависимости двух признаков, чем коэффициенты парной корреляции, так как «очищают» парную зависимость от взаимодействия данной пары переменных с другими переменными, представленными в модели. Наиболее тесно связаны 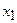и ,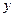 
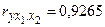. Другие взаимосвязи существенно слабее. При сравнении коэффициентов парной и частной корреляции видно, что из-за влияния межфакторной зависимости между 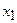и 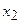происходит некоторое завышение оценки тесноты связи между переменными.
По этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи.
Пункт 2. Расчет параметров линейного уравнения множественной регрессии осуществляется обычным МНК путем решения системы нормальных уравнений. Для уравнения с двумя объясняющими переменными система примет вид:
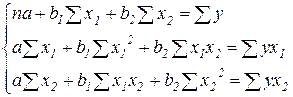
Поясните экономический смысл коэффициентов регресси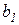и 
и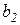 
: это показатели, характеризующие абсолютное (в натуральных единицах измерения) изменение результативного признака при изменении факторного признака на единицу своего измерения при фиксированном влиянии второго фактора.
Результаты построения уравнения множественной регрессии представлены в таблице 5.
Таблица 5. Результаты построения модели множественной регрессии
| Независимые переменные | Коэффициенты | Стандартные ошибки коэффициентов | t - статистики | Вероятность случайного значения | ||
| Константа | 44,61 | 4,58 | 9,73 | 0,0001 | ||
| x1 | 2,35 | 0,36 | 6,51 | 0,0003 | ||
| x2 | 0,16 | 0,78 | 0,21 | 0,8399 | ||
| R2 = 0,88 | ||||||
| R2adj=0,85 | ||||||
| F = 26,402 | Prob > F = 0,0005 | |||||
Уравнение имеет вид:
y = 44,61 + 2,35x1 + 0,16x2
Значения стандартной ошибки параметров представлены в графе 3 таблицы 5: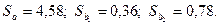 
Они показывают, какое значение данной характеристики сформировалось под влиянием случайных факторов. Их значения используются для расчета t-критерия Стьюдента (графа 4)
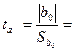9,73;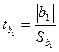 
=6,51; 
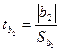=0,21.
В нашем примере параметр 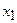является статистически значимым, а 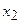- нет.[2] На это же указывает значение вероятности случайных значений параметров регрессии (графа 5), если вероятность меньше принятого за стандарт уровня a = 0,05, то делается вывод о неслучайной природе данного значения параметра, то есть о том, что он статистически значим и надежен. В противном случае принимается нулевая гипотеза (H0) о случайной природе значения коэффициентов уравнения. В нашем примере для переменной х2 a > 0,05 (aх2=0,84), что свидетельствует о малой информативности (значимости) этой переменной.
Интерпретация коэффициентов регрессии следующая:
а - оценивает агрегированное влияние прочих (кроме учтенных в модели х1 и х2) факторов на результат y;
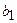и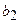 
указывают, что с увеличением х1 и х2 на единицу их значений объем продаж нового моющего средства увеличивается, соответственно, на 2,35 и 0,16 условных денежных единиц.
Пункт 3 связан с расчетом и анализом относительных показателей силы связи в уравнении множественной регрессии - частных коэффициентов эластичности. Частные коэффициенты эластичности рассчитывают, как правило, для средних значений факторного и результативного признака:
, 
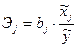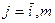
где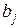 
- коэффициент условно-чистой регрессии при j-м факторе,
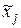- среднее значение j-го факторного признака;
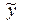- среднее значение результативного признака,
m - число факторных признаков в уравнении множественной регрессии.
Зачастую интерпретация результатов регрессии более наглядна, если произведен расчет частных коэффициентов эластичности. Частные коэффициенты эластичности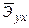 
показывают, на сколько процентов от значения своей средней 
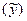изменяется результат при изменении фактора xj на 1% от своей средней 
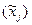и при фиксированном воздействии на y прочих факторов, включенных в уравнение регрессии. Здесь
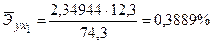
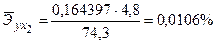
По значениям частных коэффициентов эластичности можно сделать вывод о более сильном влиянии на результат у (объем продаж моющего средства) рекламной компании по радио и телевидению, нежели демонстрации товара в магазинах.
Пункт 4 предполагает оценку совокупного влияния факторных переменных на результативный признак.
Оцените долю вариации результативного признака, объясненную совокупным влиянием факторных признаков, рассчитав совокупный (нескорректированный) множественный коэффициент детерминации:
,
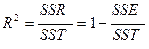где SSR=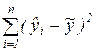 
- факторная, или объясненная моделью регрессии, сумма квадратов,
SST =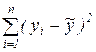 
- общая сумма квадратов,
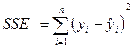- остаточная, или не объясненная моделью регрессии сумма квадратов.
В нашем примере эта доля составляет 88,29% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов. Иными словами, на весьма тесную связь факторов с результатом.
Скорректированный множественный коэффициент детерминации
(где n – число наблюдений, m – число объясняющих переменных) определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую детерминированность результата y в модели факторами x1 и x2.
Пункт 5 Охарактеризуйте степень тесноты связи между результативным признаком и всеми факторными, включенными в уравнение регрессии, определив множественный коэффициент корреляции:
.
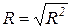Задача 3 посвящена теме «Временные ряды в эконометрических исследованиях».
Рассмотрим методику решения задачи на практическом примере:
Имеются следующие данные о расходах семьи на товар "А" в 1994-1999 гг.:
| Годы | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| Расходы на товар "А", руб. | 30 | 35 | 39 | 44 | 50 | 53 |
Приступая к выполнению пункта 1, изучите вопрос об измерении автокорреляции уровней временного ряда.
Коэффициент автокорреляции первого порядка есть линейный коэффициент корреляции между уровнями исходного временного ряда и уровнями того же ряда сдвинутыми на один момент времени.
Его расчет производится по стандартным формулам для расчета линейного коэффициента корреляции:
,
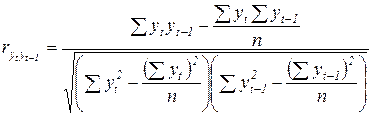где yt - 1 - уровни, сдвинутые по отношению к уровням исходного ряда на 1 год.
Заметим, что расчет должен быть осуществлен для пар наблюдений (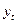 
, 
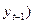, причем общее число пар наблюдений, по которым производится расчет, равно (n - 1). Близкое по абсолютной величине к единице значение коэффициента автокорреляции первого порядка свидетельствует о высокой тесноте связи между текущими и непосредственно предшествующими уровнями временного ряда или, иными словами, о наличии во временном ряде тенденции.
В соответствии с условиями нашей задачи проведем расчеты
| yt | yt+1 | ytyt+1 | yt2 | yt+12 | |
| 1994 | 30 | 35 | 1050 | 900 | 1225 |
| 1995 | 35 | 39 | 1365 | 1225 | 1521 |
| 1996 | 39 | 44 | 1716 | 1521 | 1936 |
| 1997 | 44 | 50 | 2200 | 1936 | 2500 |
| 1998 | 50 | 53 | 2650 | 2500 | 2809 |
| Суммы | 198 | 221 | 8981 | 8082 | 9991 |
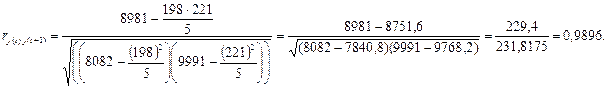
Коэффициент автокорреляции первого порядка равен 0,9896, что свидетельствует о тесной прямой связи между текущими и непосредственно предшествующими уровнями временного ряда.
В пункте 2 требуется определить функциональную форму и найти параметры уравнения, наилучшим образом описывающего тенденцию (тренд). Для определения вида тренда рассчитайте следующие показатели динамики:
а)цепные абсолютные приросты: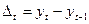 
;
б)абсолютные ускорения уровней ряда, или вторые разности: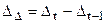 
;
в)цепные коэффициенты роста: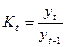 
.
Проанализируйте полученные результаты.
Если приблизительно одинаковы цепные абсолютные приросты, то для описания тенденции временного ряда следует выбрать линейный тренд: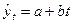 
.
Если примерно постоянны абсолютные ускорения уровней ряда, следует выбрать параболу второго порядка: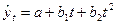 
.
Если примерно одинаковы цепные коэффициенты роста, моделирование тенденции следует проводить с использованием экспоненциальной кривой: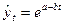 
.
Для расчета параметров уравнения тренда примените обычный МНК. В случае нелинейных зависимостей проведите линеаризацию исходной функции.
Дайте интерпретацию параметров тренда.
Коэффициент регрессии b в линейном тренде есть средний за период цепной абсолютный прирост уровней ряда.
В экспоненциальной функции величина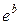 
представляет собой средний за период цепной темп роста уровней ряда.
Начальный уровень ряда в момент (период времени) t = 0 в линейном тренде выражается параметром а, в экспоненциальном тренде - величиной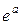 
.
Для нашей задачи проведем следующие расчеты:.
| yt |  | |  | |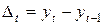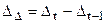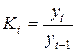
| 1994 | 30 | |||
| 1995 | 35 | 5 | 1,1667 | |
| 1996 | 39 | 4 | -1 | 1,1143 |
| 1997 | 44 | 5 | 1 | 1,1282 |
| 1998 | 50 | 6 | 1 | 1,1364 |
| 1999 | 53 | 3 | -3 | 1,0600 |
Очевидно, в данном случае для описания тренда можно выбрать линейную модель: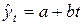 
.
Для расчета параметров уравнения тренда применим обычный МНК.
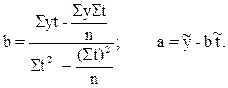
Если периоды или моменты времени пронумеровать так, чтобы получилось St =0, то вышеприведенные алгоритмы существенно упростятся и превратятся в
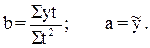
Расчеты проведем в следующей рабочей таблице.
| t | yt | t2 | ytt | |
| 1994 | -2,5 | 30 | 6,25 | -75 |
| 1995 | -1,5 | 35 | 2,25 | -52,5 |
| 1996 | -0,5 | 39 | 0,25 | -19,5 |
| 1997 | 0,5 | 44 | 0,25 | 22 |
| 1998 | 1,5 | 50 | 2,25 | 75 |
| 1999 | 2,5 | 53 | 6,25 | 132,5 |
| Суммы | 0,00 | 251 | 17,5 | 82,5 |
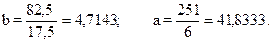
Таким образом, трендовое линейное уравнение регрессии имеет вид:
.
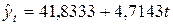Дадим интерпретацию параметров тренда.
Коэффициент регрессии (b) в линейном тренде показывает средний за период цепной абсолютный прирост уровней ряда. В нашем примере b = 4,7143, следовательно расходы на товар "А" в среднем за год увеличиваются на 4,7143 руб. Свободный член (а) в линейном тренде выражает начальный уровень ряда в момент (период времени) t = 0. В нашей нумерации t = 0 приходится на период времени между 1996 и 1997 гг., что несколько затрудняет его интерпретацию. В нашем случае а = 41,8333 руб. – это расходы семьи на товар "А" за вторую половину 1996 и первую половину 1997 гг.
В случае нелинейных зависимостей необходимо провести линеаризацию исходной функции.
Пункт 3. Точечный прогноз по уравнению тренда - это расчетное значение переменной 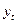, полученное путем подстановки в уравнение тренда соответствующих значений t. Интервальный прогноз рассчитывается в соответствии с методикой, изложенной для уравнения парной линейной регрессии (см. указания к пункту 5 задачи 1).
Дадим прогноз расходов на товар "А" на 2000 год.
В нашей нумерации 2000 год соответствует моменту времени t = 3,5. Отсюда,
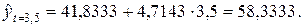
Следовательно, точечная оценка расходов семьи на товар "А" на 2000 год составляет 58,3333 руб.
Определим границы доверительного интервала, в котором с заданной надежностью γ будут находится расходы семьи на товар "А" в 2000 году. Общепринятый в экономике уровень надежности γ = 1 - α = 1 - 0,05 = 0,95.
,
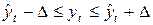где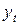 
-прогноз значения переменной y на момент (период) времени t;
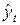- точечная оценка значения переменной y на момент (период) времени t;
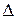- предельная ошибка прогноза.
Для того, чтобы получить интервальную оценку, определим величину предельной ошибки прогноза.
Она рассчитывается по формуле:
,
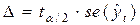где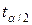 
- табличное значение t - критерия Стьюдента для уровня значимости α и числа степеней свободы (k = n - 2);
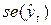- стандартная ошибка точечного прогноза, которая, в свою очередь, рассчитывается по формуле:
,
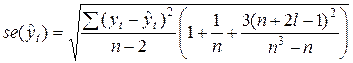где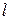 
- длина периода упреждения (срок прогноза).
Расчеты проведем в рабочей таблице.
| t | | |  |  | |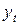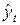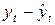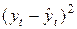
| 1994 | -2,5 | 30 | 30,0476 | -0,0476 | 0,0023 |
| 1995 | -1,5 | 35 | 34,7619 | 0,2381 | 0,0567 |
| 1996 | -0,5 | 39 | 39,4762 | -0,4762 | 0,2268 |
| 1997 | 0,5 | 44 | 44,1905 | -0,1905 | 0,0363 |
| 1998 | 1,5 | 50 | 48,9048 | 1,0952 | 1,1995 |
| 1999 | 2,5 | 53 | 53,6190 | -0,6190 | 0,3832 |
| Суммы | 0,00 | 251 | 197,3810 | 0,0000 | 1,9048 |
