Пересечение прямой с поверхностью
Пересечение прямой с поверхностью также является фундаментальной позиционной задачей. Кроме того, она входит как составной элемент в решение более сложных позиционных задач, таких, как пересечение плоскости с поверхностью, пересечение поверхностей и построение теней.
Принцип, лежащий в основе решения задачи на определение точки пересечения прямой с плоскостью, сохраняется и в случае определения общих точек прямой и поверхности (рис. 229, 230, 231). Через прямую l проводится вспомогательная плоскость l, которая пересекает поверхность по вспомогательному сечению l*. Это сечение, пересекаясь с заданной прямой l, выделяет на ней искомые точки M и N.
Поскольку через прямую l можно провести бесконечно много плоскостей, выберем такие, с которыми удобно работать. Критерием такого удобства является:
1. Графически простое сечение поверхности вспомогательной плоскостью.
2. Проецирующее положение вспомогательной плоскости.
Решение задачи рекомендуется проводить по следующему алгоритму:
1) определить, какие сечения поверхности представляют собой графически простые линии;
2) через заданную прямую и один из центров проецирования провести секущую плоскость l так, так чтобы она пересекала поверхность по графически простой линии l* (если это возможно);
3) осуществить построение точек пересечения прямой l с полученным сечением l*.
На рис. 229 приведен пример построения точек пересечения прямой l с пирамидой TABC. Прямая l занимает общее положение. Вспомогательная секущая плоскость l содержит прямую l и проходит через центр проецирования S1. Сечение l* представляет собой многоугольник. Если вспомогательная секущая плоскость пройдет через центр S2 , то решение задачи принципиально не изменится. Изменится только форма многоугольника, полученного от сечения плоскостью l.
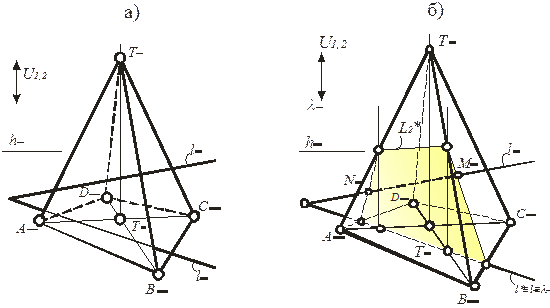
Рис. 229. Определение точки пересечения прямой с поверхностью на плоской модели (перспектива)
Проецирующее положение прямой l дано в примере на рис. 230, где l содержит центр S1 и пересекает конус. Из бесконечного множества плоскостей выберем ту, которая даст самое простое коническое сечение – прямую AT. Это плоскость l, проходящая через вершину Т, которая пересечет еще и основание конуса по прямой AB. Эти две прямые входят в часть сечения l*, позволяющего выявить точки , общие как для конуса так и для прямой l.
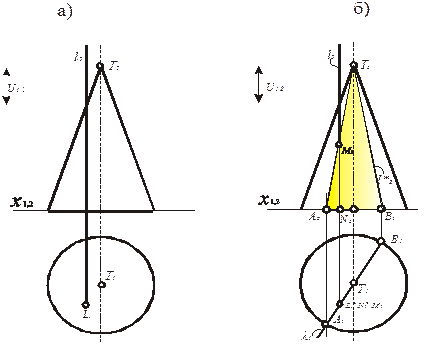
Рис. 230. Определение точки пересечения проецирующей прямой с поверхностью на плоской модели (эпюр Монжа,)
Если поверхность занимает проецирующее положение, плоскость l можно не проводить. Общие точки видны сразу на той картине, на которой поверхность вырождается в линию. В примере на рис. 231 проецирующее положение занимает цилиндр. Его вершина тождественно совпадает с центром проецирования S1, и первая проекция вырождается в линию. Её достаточно пересечь с l1, чтобы получить точки M и N, в которых прямая l пересекает цилиндр. Хотя в этом случае секущая плоскость l все-таки существует. Она проходит через центр S1 и прямую l.
Сравнивая алгоритмы решения задачи на пересечение прямой с плоскостью и с поверхностью, мы видим, что они не имеют принципиального различия. Оно возникает только тогда, когда речь заходит о вспомогательном сечении. На поверхности это сложная линия, а на плоскости – прямая.
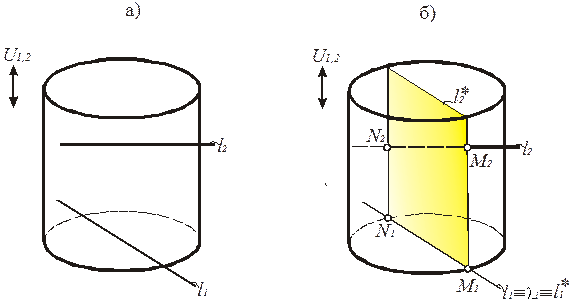
Рис. 231. Определение точки пересечения прямой общего положения с проецирующей поверхностью на плоской модели (аксонометрия)
Пересечение плоскостей
Другой часто встречающейся позиционной задачей является построение линии пресечения плоскостей. На рис. 232 приведены примеры решения этой задачи в перспективе, аксонометрии и на эпюре Монжа. Даны две плоскости a = A È В È С и b = m Ç n. В случае на рис. 232,а обе плоскости занимают общее положение. В этом случае линия пересечения l определяется по двум точкам M и N, в которых прямые m и n, принадлежащие плоскости b, пересекают плоскость a. Очевидно, что для определения этих точек необходимо два раза решить задачу на пересечение прямой с плоскостью.
Если одна из плоскостей занимает проецирующее положение, то решение задачи несколько упрощается, так как одна из проекций l тождественно совпадает с вырожденной проекцией плоскости. В примере на рис. 232,б проецирующее положение занимает плоскость b. Она содержит центр проецирования S1 и ее вторая проекция представляет собой прямую линию, с которой тождественно совпадает вторая проекция линии пересечения.
В случае когда обе плоскости содержат один и тот же центр проецирования, то через тот же центр пройдет и линия пересечения. На рис. 232,в плоскости a и b обе содержат центр S.1 , через него пройдет и линия пересечения плоскостей.
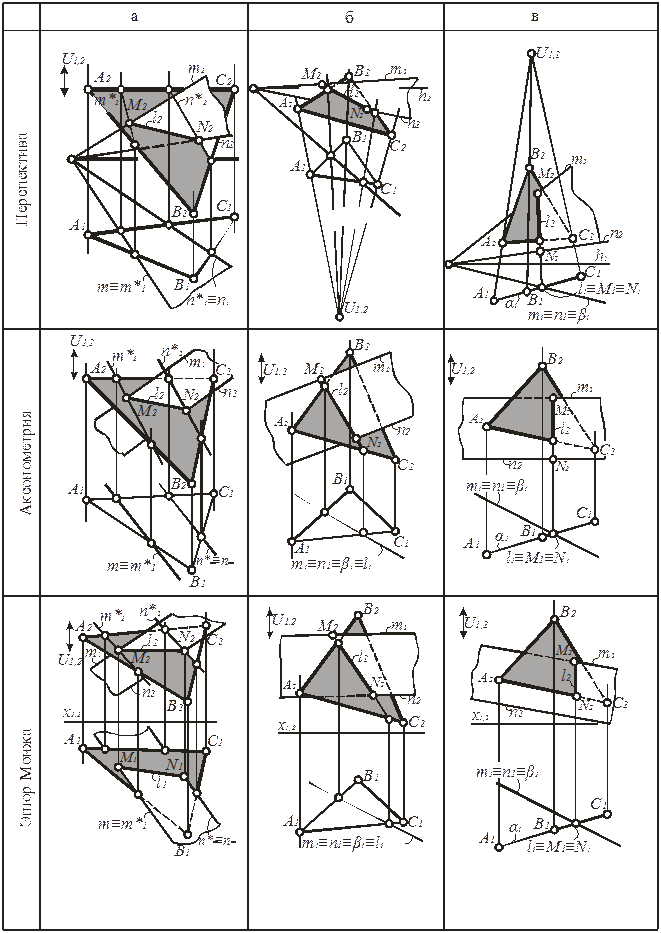Рис.232. Пересечение плоскостей