Функция нескольких переменных.

Тема : Функция нескольких переменных.

Факт исходный для мат.анализа – всякий реальный процесс описывают несколько переменных величин и они взаимозависимы. Простейший случай: зависимость двух величин – аргумента и функции. Более сложный случай – зависимость одной величины сразу от нескольких аргументов, что приводит к понятию функции нескольких переменных (ФНП) y = f(x₁, x₂, . . . , x_n).

Набор из n величин (x₁, x₂, . . . , x_n)можно отождествить с точкой n – мерного линейного пространства Rⁿ. R² –точки плоскости,R³ -точки трехмерного пространства

Опр.Функцией n – переменных y = f(x₁, x₂, . . . , x_n),определенных на множестве D Ì Rⁿи принимающей значения на множестве Y Ì R,наз. правило соответствия между элементами множеств DиY, при котором для любой точки(x₁, x₂, . . . , x_n)Î Dсуществует единственный элемент yÎ Y.

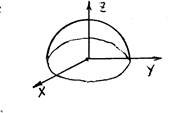Множество D наз. областью определения (ООФ), Y –областью значений функции. Так, функция двух переменных z = f(x,y) : (x.y)Î D Ì R², z Î Z Ì R.Переменные x, y, zможно понимать как координаты трехмерного пространства, тогда графиком функции z = f(x,y)является однослойная поверхность в пространстве.

Пр.1 ,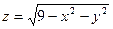

D: 9 – x² – y² > 0 , x² + y² < 3² -круг радиуса 3

Z:верхняя полусфера R = 3

Для изучения характера изменения такой функции удобно рассматривать линии уровня заданные уравнением f(x,y) = с. При движении вдоль такой линии значение функции сохраняется. Пр.1 уравнение x² + y² = сопределяет семейство окружностей.

Для функции трех переменных u = f(x,y,z)ООФ есть множество точек пространства или некоторое тело в нем. Наглядно изобразить функцию уже не удается, но в ООФ можно выделить поверхности уровня, которым соответствует постоянное значение функции f(x,y,z) = с.

Пр.2 u = 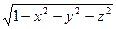, D: x² + y² + z² < 1- шар R = 1 с центром в О(0,0,0)

Функции двух переменных.

Изучать ФНП удобно на примере двух переменных, в силу их геометрической наглядности, и полученные результаты обобщить на произвольное n .

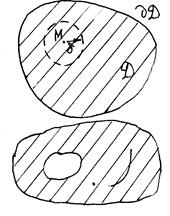ООФ z = f(x,y)задается на плоскости D Ì R²и может быть ограничена некоторой кривой L , которая наз. границей области Dи обозначается ¶D. Если область Dограничена замкнутой и не самопересекающейся линией, то она наз. односвязной. Если Dограничивают несколько замкнутых линий, то наз. многосвязной. В качестве дополнительного контура может быть точка или линия. Точки (x,y) ,принадлежащие D ,но не ¶Dназ. внутренними, а точки принадлежащие границе граничными. Область Dназ. открытой, если содержит только внутренние точки, и наз. замкнутой (D) , если включает и внутренние и внешние точки. Круг радиуса d вокруг точки М наз. d-окрестностью этой точки.

Предел и непрерывность ФНП.

Опр.Пределом функции z = f(x,y)при стремлении т. М(х,у) к т. М₀(х₀,у₀) наз. число Атакое, что разность между ним и значением функции f(x,y)делается б.м.в. при М®М₀

lim [f(x.y) – A] = 0или lim f(x,y) = Aпри М ® М₀ ( 1 )

Достаточное условие существования функции в точке(по Коши).

Пусть точкам M(x,y)из некоторой d-окрестности точки М₀соответствуют значения z из e-окрестности точки А. В том случае, если между границами этих окрестностей существует четкая связь d = d(e) , то сжатие круга вокруг точки М₀автоматически приводит к сжатию интервала вокруг точки Аи предельный процесс М ® М₀влечет за собой предельный процесс z ® A. Таким образом, для установления факта существования предела функции z ® Aдостаточно убедится в существовании зависимости между e > 0 и d>0 , при которой выполняются неравенства:

если |M₀M| < d , то |f(x,y) – A| < e.( 2 )

Теоремы о пределах функции одной переменной справедливы и для ФНП. Предел от константы равен константе. Предел от суммы, произведения, частного двух функций равен сумме, произведению, отношению пределов и т.д.

Опр.Функция z = f(x,y)наз. непрерывной в точке М₀(х₀,у₀), если она определена и в ее окрестности и предел функции при М ® М₀равен значению функции в точке М₀ :

lim f(x,y) = f(x₀,y₀)при М ® М₀ ( 3 )

Опр. Функция z = f(x,y)наз. непрерывной на некотором множестве E Ì D,если она непрерывна в каждой точке этого множества.

Опр.Точка М₀(х₀,у₀)наз. точкой разрыва, если в ней нарушается хотя бы одно из условий непрерывности. Точки разрыва могут быть изолированными или образовывать линии.

Пр. z = xy / (x – y) . y = x -линия разрыва.

Частные приращения и частные производные.

Опр.Частным приращением функции z = f(x,y)по хназ. разность

D_хz = f(x+Dx,y) – f(x,y),частным приращением по y - D_yz = f(x,y+Dy) – f(x,y) .

Опр.Частной производной по х от функции z = f(x,y)наз. предел отношения частного приращения D_хzк приращению Dхпри стремлении его к нулю :

z`_x = ¶z / ¶x = lim D_хz / Dxпри Dx ® 0( 4 )

Аналогично для переменной y : z`_y = ¶z / ¶y = lim D_yz / Dпри Dy ® 0

Произведения z`<sub>x</sub>dxиz`_ydyназ. частными дифференциалами. Частные приращения и частные производные для функций с произвольным числом аргументов определяются аналогичным образом.

Правила вычисления частных производных : частная производная от z = f(x,y)по х есть обычная производная по х условии y = const.При вычислении частной производной по y , наоборот, x = const.

Геометрический смысл частных производных. Условие y = constпри вычислении z`_x

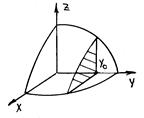означает, что производится сечение поверхности z = f(x,y)плоскостью y = y₀^ оси Оу, которое дает плоскую кривую z = f(x,y₀) . Таким образом, производная z`<sub>x</sub>определяет скорость изменения функции вдоль этой кривой или тангенс угла наклона касательной к ней. Производная z`_yсвязана с сечением поверхности ^ оси Ох (x = x₀).

Полное приращение и полный дифференциал

Опр.Полным приращением функции z = f(x,y)наз. результат одновременного изменения всех аргументов, т.е. разность z = f(x+ x, y+ y) – f(x,y).

Полное приращение не является простой суммой частных приращений и может содержать xи yкак в первой, так и в более высоких степенях.

Пр. z = xy. _х z = y x , _y z = x y , z = _х z + _y z + x y

По определению, дифференциалом функции одной переменной y = f(x)является главная часть приращения функции, линейная по x : y = А x + 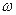( x).Причем,

dy = А x = f (x) dx ,а 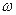( x)– более высокого порядка малости по x.