ТЕМА № 2. СИСТЕМЫ СЧИСЛЕНИЯ
Понятие о системе счисления. Запись чисел в позиционных системах. Операции над целыми неотрицательными числами в позиционной системе счисления.
Литература: [1] с. 271-288, [2] с. 143-145, [3] с. 129-149, [4] с. 66-69, [5] с. 136-142, [6] с.122-126, [7] с. 136-156.
СИСТЕМЫ СЧИСЛЕНИЯ
(задания I уровня)
1А. Среди следующих сумм найдите краткую запись числа 700258:
а) 7・104 + 2・10 + 5;
б) 7・103 + 2・102 + 5・10;
в) 7・84 + 2・8 + 5;
г) 7・82 + 2・8 + 5.
1Б. Замените суммы краткой записью числа:
а) 6・102 + 5・10 + 1; б) 3・43 + 2・4; в) 1・26 + 1・24 + 1.
2А. Среди следующих сумм найдите краткую запись числа 1001112:
а) 1・103 + 1・102 + 1・10;
б) 1・25 + 1・104 + 1・103 + 1;
в) 1・25 + 1・23 + 1・22 + 1・2;
г) 1・25 + 1・22 + 1・2 + 1.
2Б. Замените суммы краткой записью числа:
а) 3・52 + 1・5 + 2; б) 7・84 + 6・83 + 4; в) 2・34 + 1・32 + 2.
3А. Среди следующих сумм найдите краткую запись числа 1210223:
а) 1・106 + 2・105 + 1・104 + 2・103 + 2・10;
б) 1・36 + 2・35 + 1・34 + 2・32 + 2・3;
в) 1・35 + 2・34 + 1・33 + 2・3 + 2;
г) 1・105 + 2・104 + 1・103 + 2・10 + 2.
3Б. Замените суммы краткой записью числа:
а) 3・82 + 7・8 + 4; б) 1・25 + 1・23 + 1 ・2 + 1; в) 3・54 + 2・53 + 4.
4А. Среди следующих сумм найдите краткую запись числа 2103314:
а) 2・105 + 1・104 + 3・103 + 3・102 + 1・10;
б) 2・45 + 2・44 + 3・43 + 3・42 + 1・4;
в) 2・45 + 2・44 + 3・42 + 3・4 + 1;
г) 2・105 + 2・104 + 3・102 + 3・10 + 1.
4Б. Замените суммы краткой записью числа:
а) 3・72 + 5・7 + 2; б) 2・45 + 1・44 + 3・43 + 3・42 + 1; в) 4・65.
5А. Среди следующих сумм найдите краткую запись числа 423105:
а) 4・104 + 2・103 + 3・102 + 1・101;
б) 4・54 + 2・43 + 3・42 + 1・10;
в) 4・53 + 2・102 + 3・5 + 1;
г) 4・54 + 2・53 + 3・52 + 1・5.
5Б. Замените суммы краткой записью числа:
а) 2・35 + 1・33 + 2・3 + 1; б) 4・56 + 2・53 + 5; в) 7・96.
0А. Среди следующих сумм найдите краткую запись числа 165037:
а) 1・74 + 6・73 + 5・72 + 3;
б) 1・74 + 6・73 + 5・72 + 3・7;
в) 1・104 + 6・103 + 5・102 + 3;
г) 1・103 + 6・102 + 5・10 + 3.
Решение:
165037 = 1 · 74 + 6 · 73 + 5 · 72 + 0 · 7 + 3 = 1 · 74 + 6 · 73 + 5 · 72 + 3, поэтому а) – верно; б) – не верно; в) и г) также не верно, т.к. число записано в системе счисления с основанием р = 7.
0Б. Замените суммы краткой записью числа:
а) 5・102 + 2 ; б) 3・94 + 6・92 + 1・9 + 7; в) 1・26 + 1・24 + 1・2.
Решение:
а) 5・102 + 2 = 502
б) 3・94 + 6・92 + 1・9 + 7 = 306179
в) 1・26 + 1・24 + 1・2 = 10100102
СИСТЕМЫ СЧИСЛЕНИЯ
(задания II уровня)
1А. Верно ли, что в числе 25760 всего:
а) 25 тысяч; б) 7 сотен; в) 257 сотен; г) 2576 десятков; д) 6 десятков?
1Б. Запишите число, в котором: а) 56 миллионов и 23 десятка; б) 32 тысячи и 364 единицы; в) 605 десятков тысяч, 32 сотни и 24 единицы.
2А. Верно ли, что в числе 362100 всего:
а) 36 тысяч; б) 362 тысячи; в) 36 десятков тысяч; г) 100 единиц; д) 3621 сотня?
2Б. Запишите число, в котором: а) 179 сотен тысяч и 22 десятка; б) 41 десяток тысяч и 88 десятков; в) 55 тысяч и 714 единиц.
3А. Верно ли, что в числе 197324 всего:
а) 197 тысяч; б) 1973 сотни; в) 324 единицы; г) 19732 десятка; д) 19 десятков тысяч?
3Б. Запишите число, в котором: а) 21 сотня тысяч и 996 десятков; б) 42 миллиона, 302 десятка тысяч и 17 единиц; в) 825 сотен тысяч.
4А. Верно ли, что в числе 76809 всего:
а) 768 десятков; б) 7680 десятков; в) 76 тысяч; г) 768 сотен; д) 76809 единиц?
4Б. Запишите число, в котором: а) 506 сотен тысяч; б) 23 десятка миллионов, 825 сотен и 31 единицы; в) 101 тысяча и 332 сотни.
5А. Верно ли, что в числе 2170302 всего:
а) 21 сотня тысяч; б) 217 десятков тысяч; в) 170 тысяч; г) 21703 сотни; д) 2170 тысяч?
5Б. Запишите число, в котором: а) 178 десятков миллионов; б) 34 десятка тысяч, 42 десятка и 815 единиц; в) 75 сотен и 382 десятка.
0А. Верно ли, что в числе 3006158 всего:
а) 3 миллиона; б) 6 тысяч; в) 3006 тысяч; г) 30061 сотня; д) 615 десятков?
Решение:
а) верно;
б) нет, не верно, т.к. чтобы узнать, сколько в числе тысяч, нужно закрыть последние три цифры, полученное число и есть число тысяч в данном числе;
в) верно;
г) верно;
д) нет (объяснение аналогично пункту б).
0Б. Запишите число, в котором: а) 24 миллиона и 605 сотен; б) 87 десятков тысяч, 90 сотен и 814 единиц; в) 506 десятков миллионов.
Решение:
а) 24060500;
б) 879814;
в) 5060000000.
СИСТЕМЫ СЧИСЛЕНИЯ
(задания III уровня)
1А. Переведите числа: а) 75428, 1110112 в десятичную систему счисления; б) 12937 в систему счисления с основанием р=7; р=3.
1Б. Найдите сумму и разность чисел, а затем выполните проверку с использованием десятичной системы счисления: 15436 и 2456.
2А. Переведите числа: а) 2320104, 6543217 в десятичную систему счисления; б) 43728 в систему счисления с основанием р=6; р=4.
2Б. Найдите сумму и разность чисел, а затем выполните проверку с использованием десятичной системы счисления: 4268 и 3528.
3А. Переведите числа: а) 4320015, 2100223 в десятичную систему счисления; б) 17931 в систему счисления с основанием р=7; р=5.
3Б. Найдите сумму и разность чисел, а затем выполните проверку с использованием десятичной системы счисления: 10207 и 5347.
4А. Переведите числа: а) 101011002, 251189 в десятичную систему счисления; б) 6122 в систему счисления с основанием р=2; р=4.
4Б. Найдите сумму и разность чисел, а затем выполните проверку с использованием десятичной системы счисления: 10102 и 1112.
5А. Переведите числа: а) 7100628, 131224 в десятичную систему счисления; б) 7432 в систему счисления с основанием р=3; р=7.
5Б. Найдите сумму и разность чисел, а затем выполните проверку с использованием десятичной системы счисления: 4235 и 3445.
0А. Переведите числа: а) 261337, 120113 в десятичную систему счисления; б) 26104 в систему счисления с основанием р=2; р=8.
Решение:
а) 261337 = 2・74 + 6・73 + 1・72 + 3・7 + 3 = 4802 + 2058 + 49 +
+ 21 + 3 = 6933
120113 = 1・34 + 2・33 + 0・32 + 1・3 + 1 = 81 + 54 + 3 + 1 = 139
Ответ: 261337 = 6933; 120113 = 139
б)
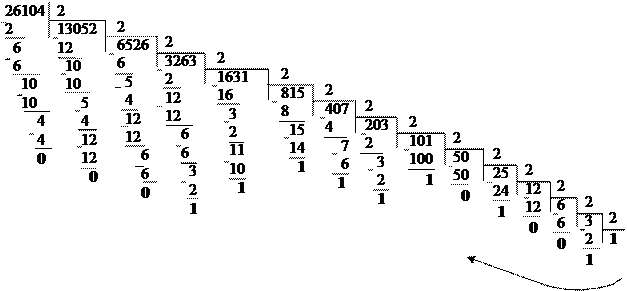
26104=1100101111110002
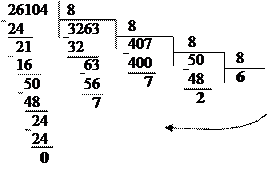 |
26104=627708
Ответ: 26104=1100101111110002
26104=627708
0Б. Найдите сумму и разность чисел, а затем выполните проверку с использованием десятичной системы счисления: 7368 и 2528.
Решение:
| + | 7368 | – | 7368 | |
| 2528 | 2528 | |||
| 12108 | 4648 |
Для проверки переведем числа из восьмеричной системы счисления в десятичную. Для этого запишем числа 7368 и 2528 в виде суммы разрядных слагаемых и выполним арифметические действия в десятичной системе счисления.
7368 = 7・82 + 3・81 + 6・80 = 448 + 24 = 478
2528 = 2・82 + 5・81 + 2・80 = 128 + 40 + 2 = 170
| + | – | |||
Переведем числа 648 и 308 из десятичной системы счисления в восьмеричную.
 | 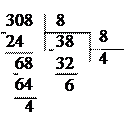 | ||
648 = 12108 308 = 4648
Ответ: 12108; 4648.
СИСТЕМЫ СЧИСЛЕНИЯ
(задания IV уровня)
1А. Найдите значение выражения: 232135 : 325 – 1135.
1Б. Решите уравнение: 122х + 201х = 36.
2А. Найдите значение выражения: 1326・476 + 24516.
2Б. Решите уравнение: 322х + 231х = 103.
3А. Найдите значение выражения: (14727 –5137)・4137.
3Б. Решите уравнение: 212х – 101х = 13.
4А. Найдите значение выражения: (1324 + 2124) ・134.
4Б. Решите уравнение: 45х ・23х = 561.
5А. Найдите значение выражения: 7318 : 138 + 6118.
5Б. Решите уравнение: 43х : 13х = 3.
СИСТЕМЫ СЧИСЛЕНИЯ
(задания V уровня)
1А. Найдите значение выражения: 112・112+125・135.
1Б. Сумма цифр двузначного числа равна 7. Если к каждой цифре прибавить 2, то получится число, которое на 3 меньше удвоенного первоначального числа. Найдите это число.
2А. Найдите значение выражения: 7318 : 138+1135・35.
2Б. Двузначное число, деленное на сумму его цифр, дает в частном 4 и в остатке 3. Если переставить цифры в этом числе, то получим число, на 5 больше, чем увеличенная в 6 раз сумма его цифр. Найдите это число.
3А. Найдите значение выражения: 21345 : 125+578・378.
3Б. Произведение цифр двузначного числа в три раза меньше самого числа. Если к искомому числу прибавить 18, то получится число, записанное теми же цифрами, но в обратном порядке. Найдите это число.
4А. Найдите значение выражения: 1213・223 – 256・136.
4Б. Найдите двузначное число по следующим условиям: частное от деления искомого числа на сумму его цифр равно 8; частное от деления на ту же сумму произведения его цифр равно 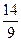 .
.
5А. Найдите значение выражения: 768・648 – 232136 : 3266.
5Б. Сумма квадратов цифр двузначного числа равна 10, а произведение искомого числа на число, записанное теми же цифрами, но в обратном порядке, равно 403. Найдите число.
