Что принципиально важно в оформлении решения?

Во-первых, указываем неопределенность, если она есть.

Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.

В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:

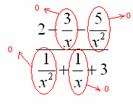
Для пометок лучше использовать простой карандаш.

Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметить недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?

Пример 2

Найти предел .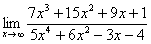

Снова в числителе и знаменателе находим 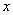в старшей степени:

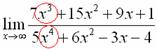
Максимальная степень в числителе: 3

Максимальная степень в знаменателе: 4

Выбираем наибольшее значение, в данном случае четверку.

Согласно нашему алгоритму, для раскрытия неопределенности 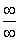делим числитель и знаменатель на .

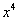Полное оформление задания может выглядеть так:

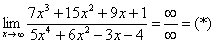
Разделим числитель и знаменатель на :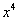

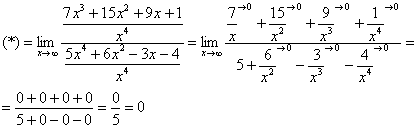
Пример 3

Найти предел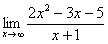

Максимальная степень «икса» в числителе: 2

Максимальная степень «икса» в знаменателе: 1 ( 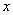можно записать как )

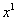Для раскрытия неопределенности 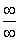необходимо разделить числитель и знаменатель на 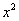. Чистовой вариант решения может выглядеть так:

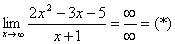
Разделим числитель и знаменатель на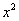

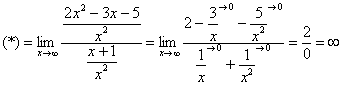
Под записью 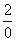подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.

Таким образом, при раскрытии неопределенности вида 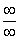у нас может получиться конечное число, ноль или бесконечность.

6.1.2. Пределы с неопределенностью вида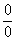 и метод их решения

Группа следующих пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.

Пример 4

Решить предел

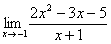
Сначала попробуем подставить -1 в дробь:

.

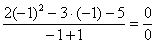В данном случае получена так называемая неопределенность .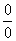

Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 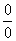, то для ее раскрытия нужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицыи ознакомьтесь с методическим материалом Горячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.

Итак, решаем наш предел

.

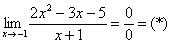Разложим числитель и знаменатель на множители

Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:

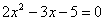
Сначала находим дискриминант:

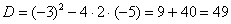
И квадратный корень из него: .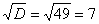

В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе. Далее находим корни:

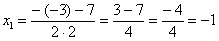
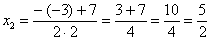
Таким образом:

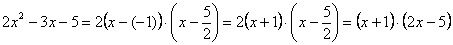
Всё. Числитель на множители разложен.

Знаменатель. Знаменатель 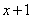уже является простейшим множителем, и упростить его никак нельзя.

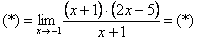
Очевидно, что можно сократить на :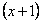

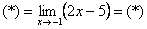
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

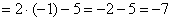
Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:

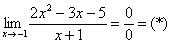
Разложим числитель на множители.

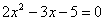
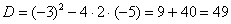
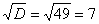
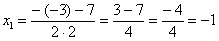
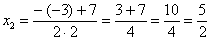
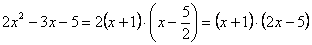
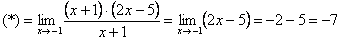
Пример 5

Вычислить предел

.

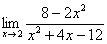Сначала «чистовой» вариант решения

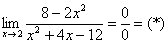
Разложим числитель и знаменатель на множители.

Числитель: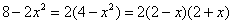
Знаменатель:



,

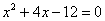
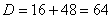
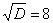
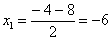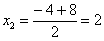
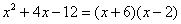
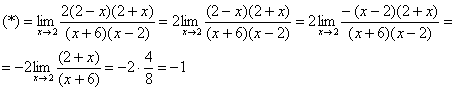
Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.

Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела.Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.

Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.

! Важно
В ходе решения фрагмент типа 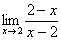встречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки).
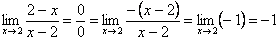, то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.

Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.