Некоторые законы распределений и их числовые характеристики
Биномиальное распределение представляет собой распределение вероятностей появления события А при n независимых испытаний, в каждом из которых событие А может осуществиться с одной и той же вероятностью P(A) = p. Кроме события A, может произойти также противоположное событие 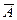 , вероятность которого P(
, вероятность которого P( 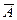 ) = 1 – p = q.
) = 1 – p = q.
Случайная величина Х распределена по биномиальному закону, если ее возможные значения есть 0, 1, 2, …, n и вероятности этих значений определяются по формуле Бернулли:
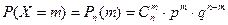 .
.
Вероятности любого числа событий соответствуют членам разложения бинома Ньютона в степени, равной числу испытаний.
Числовые характеристики биномиального распределения:
M(m) = np – математическое ожидание частоты появлений события A при n независимых испытаниях;
D(m) = npq – дисперсия частоты появления события A;
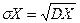 – среднее квадратическое отклонение частоты.
– среднее квадратическое отклонение частоты.
Когда число испытаний n велико, то для вычисления вероятности комбинаций используется локальная теорема Лапласа:
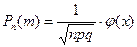 .
.
Равномерное распределение
Непрерывная случайная величина распределена равномерно на интервале (а, в), если на этом интервале ее функция плотности имеет вид
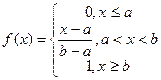 ;
; 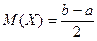 ;
; 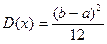 .
.
Нормальное распределение
Главная особенность нормального распределения состоит в том, что оно является предельным, к которому приближаются другие распределения.
Нормальным называется распределение, функция плотности вероятности которого имеет вид
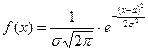 ,
,
где а – математическое ожидание,
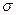 – среднее квадратическое отклонение,
– среднее квадратическое отклонение, 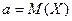 ,
, 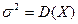 ,
, 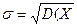 .
.
Вопросы для контроля
1. Множество событий. Классическое определение вероятности события.
2. Основные теоремы теории вероятностей. Формула Бейеса.
3. Случайные величины. Непрерывные и дискретные случайные величины.
4. Законы распределения случайных величин.
5. Двумерная случайная величина. Доверительный интервал, проверка гипотезы. Критерий Пирсона.
6. Основные понятия комбинаторики: размещения, перестановки, сочетания. Бином Ньютона.
7. Определение случайного события. Операции над случайными событиями. Несовместные события. Полная группа событий.
8. Определения вероятности (классическое, статистическое, геометрическое). Свойства вероятности.
9. Условная вероятность. Независимые и зависимые события. Формулы умножения вероятностей. Вероятность наступления хотя бы одного события.
10. Формула полной вероятности. Вероятность гипотез (формула Бейеса).
11. Схема независимых испытаний: постановка задачи, формула Бернулли, формула Пуассона.
12. Схема независимых испытаний: локальная и интегральная формулы Муавра – Лапласа. Функция Лапласа, ее свойства. Следствие из интегральной формулы Муавра – Лапласа (отклонение относительной частоты появления события от его вероятности).
13. Определение случайной величины, классификация случайных величин. Понятие закона распределения вероятностей дискретных случайных величин. Независимые случайные величины. Функции одного и двух случайных аргументов.
14. Математическое ожидание дискретной случайной величины, его свойства.
15. Дисперсия, среднее квадратическое отклонение, мода дискретной случайной величины, их свойства. Начальные и центральные моменты, асимметрия и эксцесс.
16. Функция распределения случайной величины, ее свойства. Построение графика функции распределения дискретной случайной величины.
17. Задание системы двух дискретных случайных величин, построение законов распределения ее составляющих. Числовые характеристики системы двух дискретных случайных величин: ковариационный момент, коэффициент корреляции.
18. Определение непрерывной случайной величины. Функция и плотность распределения, их свойства. Вероятность попадания непрерывной случайной величины в интервал. Числовые характеристики непрерывных случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение, медиана.
19. Равномерный и показательный законы распределения, их числовые характеристики.
20. Нормальный закон распределения, его числовые характеристики. Вероятность попадания нормально распределенной случайной величины в заданный интервал.
21. Случайные величины общего вида, их числовые характеристики.
22. Цепи Маркова, способы их представления. Вычисление вероятностей переходов за два и более шага, а также предельного распределения вероятностей.
23. Простейший (пуассоновский) поток событий, его свойства, закон распределения случайного времени между наступлениями двух событий потока.
24. Марковские случайные процессы: определение, правила составления систем дифференциальных и алгебраических уравнений относительно вероятностей состояний.
25. Системы массового обслуживания с отказами, их основные характеристики.
26. Системы массового обслуживания с ожиданием, их основные характеристики.
27. Выборочная совокупность и вариационный ряд. Вычисление объема выборки и относительных частот. Графическое представление рядов распределения: полигон или гистограмма, график эмпирической функции распределения.
28. Статистические оценки параметров распределения: понятия состоятельной и несмещенной оценки, выборочные среднее, средний квадрат, исправленные выборочные дисперсия и среднеквадратическое отклонение, интервальные оценки для математического ожидания и среднеквадратического отклонения нормального закона. Привести демонстрационные примеры расчета точечных оценок.
29. Статистическая гипотеза. Виды гипотез. Ошибки первого и второго рода. Понятия уровня значимости, критерия, критической области, виды критических областей.
30. Правила проверки гипотез о равенствах генеральной дисперсии и генерального среднего (математического ожидания) нормального закона заданным значениям.
31. Правило проверки гипотезы о подчинении эмпирической выборки равномерному закону распределения с помощью критерия Пирсона.
32. Корреляционная зависимость между переменными. Выборочный коэффициент корреляции и линейное уравнение регрессии. Проверка гипотезы о значимости выборочного коэффициента корреляции.
33. Выборочный коэффициент ранговой корреляции Спирмена, его свойства, проверка гипотезы о его значимости.
34. Выборочный коэффициент ранговой корреляции Кендалла, его свойства, проверка гипотезы о его значимости.
35. Однофакторный дисперсионный анализ. Факторная таблица. Общее и групповые средние. Проверка гипотезы о равенстве групповых средних по критерию Фишера.
36. Понятие псевдослучайной последовательности. Генерация псевдослучайных последовательностей в различных прикладных программах.
37. Генерация дискретного закона распределения, заданного в виде таблицы, с помощью псевдослучайных чисел.
38. Генерация равномерного, показательного и нормального законов распределения с помощью псевдослучайных чисел.
39. Метод Монте-Карло, его применение к вычислению определенных интегралов. Оценка наименьшего числа испытаний.
Глоссарий
Определение: Последовательностью называется функция натурального аргумента 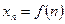 ,
, 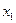 ,
, 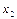 ,…,
,…, 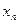 ,…,
,…, 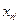 ,… .
,… .
Определение: Число 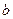 называется пределом функции
называется пределом функции 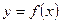 в точке
в точке  , если для любого
, если для любого 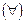 сколь угодно малого положительного числа
сколь угодно малого положительного числа 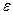 найдется
найдется 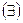 положительное число
положительное число 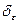 (дельта), что для всех
(дельта), что для всех 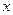 , удовлетворяющих неравенству
, удовлетворяющих неравенству 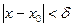 , выполнится неравенство
, выполнится неравенство 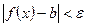 . Пишут
. Пишут 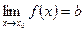 .
.
Определение: Функция 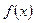 называется бесконечно малой в точке
называется бесконечно малой в точке  , если
, если 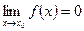 .
.
Определение: Функция 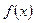 называется бесконечно большой в точке
называется бесконечно большой в точке  , если
, если 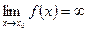 .
.
Теорема: Если 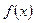 – бесконечно большая функция, то
– бесконечно большая функция, то 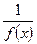 – бесконечно малая функция. Если
– бесконечно малая функция. Если 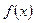 – бесконечно малая и
– бесконечно малая и 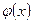 – бесконечно малая функция в точке
– бесконечно малая функция в точке  и
и 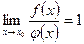 , то
, то 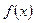 и
и 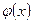 эквивалентны. Пишут
эквивалентны. Пишут 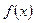 ~
~ 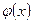 .
.
Определение: Функция 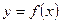 называется непрерывной в точке
называется непрерывной в точке  , если существует предел функции в точке
, если существует предел функции в точке  , равный значению функции в точке
, равный значению функции в точке  , т. е.
, т. е. 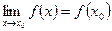 .
.
Определение: Точка  называется точкой разрыва функции
называется точкой разрыва функции 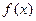 первого рода, если существуют конечные, но неравные односторонние пределы функции в точке
первого рода, если существуют конечные, но неравные односторонние пределы функции в точке  . Разность между правым и левым пределами называется скачком.
. Разность между правым и левым пределами называется скачком.
Определение: Точка  называется точкой разрыва второго рода, если хотя бы один из односторонних пределов равен
называется точкой разрыва второго рода, если хотя бы один из односторонних пределов равен 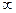 или не существует.
или не существует.
Определение: Точка  называется точкой устранимого разрыва, если существует предел функции в этой точке, не равный значению функции в точке
называется точкой устранимого разрыва, если существует предел функции в этой точке, не равный значению функции в точке  .
.
Определение: Пусть функция 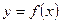 задана на некотором множестве
задана на некотором множестве 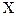 .
. 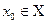 и
и 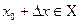 . Тогда соответствующее приращение
. Тогда соответствующее приращение 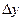 функции равно разности нового и старого значений:
функции равно разности нового и старого значений: 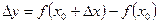 . Если существует конечный предел отношения приращения функции к приращению аргумента при
. Если существует конечный предел отношения приращения функции к приращению аргумента при 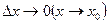 , то он называется производной функции в точке
, то он называется производной функции в точке  . Пишут
. Пишут 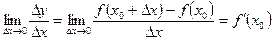 , или
, или 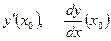 .
.
Определение: Производной второго порядка функции 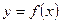 в точке называется производная от первой производной, т. е.
в точке называется производная от первой производной, т. е. 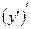 , если она существует. Обозначают
, если она существует. Обозначают 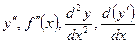 .
.
Определение: Производной n-го порядка функции 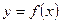 называют производную от производной (n – 1)-го порядка данной функции. Обозначают
называют производную от производной (n – 1)-го порядка данной функции. Обозначают 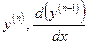 .
.
Определение: Дифференциалом функции 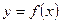 в точке
в точке  называется главная линейная часть приращения этой функции, зависящая линейно от приращения
называется главная линейная часть приращения этой функции, зависящая линейно от приращения 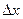 :
: 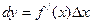 (
( 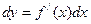 ).
).
Определение: Точки, в которых производная первого порядка обращается в нуль или терпит разрыв, называются критическими.
Определение: Прямая называется асимптотой данной кривой 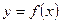 , если расстояние от точки М кривой до прямой, при удалении точки М в бесконечность, стремится к нулю.
, если расстояние от точки М кривой до прямой, при удалении точки М в бесконечность, стремится к нулю.
Если 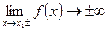 , то
, то 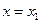 – вертикальная асимптота.
– вертикальная асимптота.
Если существуют пределы: 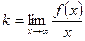 и
и 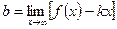 , то прямая
, то прямая 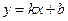 – наклонная асимптота графика функции. Если
– наклонная асимптота графика функции. Если 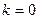 ,
, 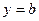 – горизонтальная асимптота.
– горизонтальная асимптота.
Определение: Число B называют пределом функции 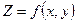 в точке
в точке 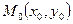 , если для любого
, если для любого 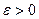 существует
существует 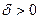 , такое, что при всех x и y, удовлетворяющих условиям
, такое, что при всех x и y, удовлетворяющих условиям 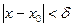 и
и 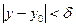 , справедливо неравенство
, справедливо неравенство  . Пишут
. Пишут 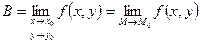 .
.
Определение:Частной производной функции 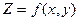 по переменной x называют предел отношения
по переменной x называют предел отношения 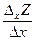 , а по переменной y –
, а по переменной y – 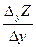 , если они существуют, тогда
, если они существуют, тогда 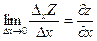 , а
, а 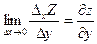 , где
, где 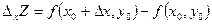 ,
, 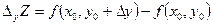 . Обозначают
. Обозначают 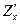 ,
, 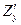 ,
, 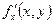 ,
, 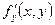 .
.
Определение: Полем называется область некоторого пространства, в каждой точке которой определено значение некоторой величины.
Определение:Если в каждой точке М этой области V соответствует определенное число j = j(М), то говорят, что в области V задано скалярное поле.
Определение:Если каждой точке М из области V соответствует некоторый вектор 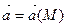 , то говорят, что задано векторное поле.
, то говорят, что задано векторное поле.
Определение:Множество точек поля, в которых скаляр j имеет одно и то же значение, называется поверхностью уровня поля.
Определение:Градиентом функции j (х, y, z) обозначают gradj , называют вектор, координатами которого являются значения частных производных функции j (х, y, z) в точке М (х, y, z): gradj = 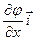 +
+ 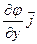 +
+ 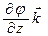 , где
, где 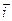 ,
, 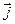 ,
, 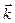 – единичные векторы, или gradj=(
– единичные векторы, или gradj=( 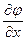 ;
; 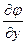 ;
; 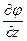 ).
).
Определение: Векторной линией поля 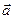 называется линия, касательная к которой в каждой ее точке М имеет направление соответствующего ей вектора поля. Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называется векторной трубкой.
называется линия, касательная к которой в каждой ее точке М имеет направление соответствующего ей вектора поля. Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называется векторной трубкой.
Определение: Предел суммы элементарных потоков через частичные области, на которые разбивается область S, когда число частичных областей неограниченно растет при условии, что наибольший из диаметров площади неограниченно убывает, называется потоком векторного поля 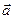 через поверхность S.
через поверхность S.
Определение:Потоком вектора 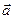 через поверхность S называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности
через поверхность S называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности
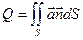 или
или 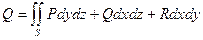 .
.
Определение:Дивергенцией векторного поля 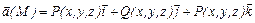 в точке М называется скаляр вектора вида
в точке М называется скаляр вектора вида 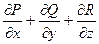 и обозначают div
и обозначают div 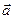
div 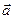 (M) =
(M) = 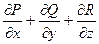 .
.
Определение:Дивергенцией векторного поля в точке М называется предел отношения потока поля через поверхность S, окружающую точку М, к объему тела, ограниченного этой поверхностью, при условии, что поверхность стягивается в точку М.
Определение:Циркуляцией вектора 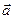 вдоль кривой L называется криволинейный интеграл по замкнутому контуру L от скалярного произведения вектора
вдоль кривой L называется криволинейный интеграл по замкнутому контуру L от скалярного произведения вектора 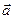 на
на 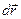 (касательный к L)
(касательный к L)
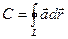 ,
,
или, учитывая, что 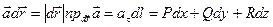 , получим
, получим 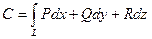 , где
, где 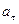 – проекция вектора
– проекция вектора 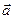 на касательную
на касательную 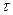 , проведенную в направлении обхода.
, проведенную в направлении обхода.
Определение:Вихревым вектором или вектором поля 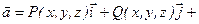 +
+ 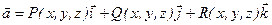 называется вектор, определенный равенством
называется вектор, определенный равенством
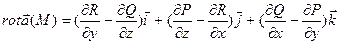
или
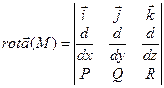 .
.
Определение:Векторными операциями первого порядка называется взятие градиента, дивергенции и ротора.
Оператор Гамильтона (символический вектор) имеет вид:
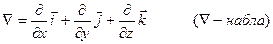 .
.
Определение: Отображение, которое каждому числу 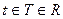 ставит в соответствие, по некоторому правилу, единственный вектор
ставит в соответствие, по некоторому правилу, единственный вектор 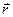 , называется векторной функцией скалярного аргумента t.
, называется векторной функцией скалярного аргумента t. 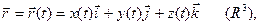 где
где 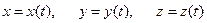 , t – параметр.
, t – параметр.
Определение: Если вектор 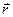 откладывать из одной точки М при различных значениях t, то конец вектора опишет в пространстве кривую, называемую годографом векторной функции
откладывать из одной точки М при различных значениях t, то конец вектора опишет в пространстве кривую, называемую годографом векторной функции 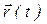 . Сама точка М называется полюсом годографа.
. Сама точка М называется полюсом годографа.
Определение: Если 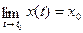
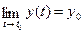
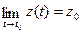 ,то
,то 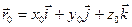 называется пределом вектор-функции
называется пределом вектор-функции 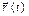 в точке t = t0, пишут
в точке t = t0, пишут 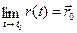 .
.
Определение: Если существует предел 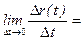
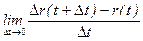 , то он называется производной вектор-функции
, то он называется производной вектор-функции 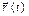 в точке t и обозначается
в точке t и обозначается 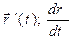 .
.
Определение: Вектор 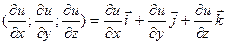 называется градиентом дифференцируемой функции u = f (x, y, z) в точке М и обозначается grad u .
называется градиентом дифференцируемой функции u = f (x, y, z) в точке М и обозначается grad u .
Определение: Дивергенцией векторного поля 
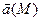 в точке М обозначается div
в точке М обозначается div 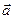 (M), называется величина, равная сумме частных производных, вычисленных в точке М.
(M), называется величина, равная сумме частных производных, вычисленных в точке М.
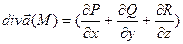 .
.
Определение:Ротором или вихрем векторного поля 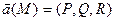 называется вектор
называется вектор 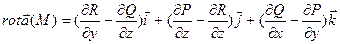 .
.
Определение: Циркуляция векторного поля 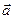 (М) вдоль замкнутого контура Г равна потоку ротора этого поля через любую гладкую поверхность S, ограниченную контуром Г. Обозначается:
(М) вдоль замкнутого контура Г равна потоку ротора этого поля через любую гладкую поверхность S, ограниченную контуром Г. Обозначается: 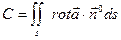 – формула Стокса.
– формула Стокса.
Определение: Плотностью циркуляции векторного поля 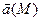 в точке М называется число, равное
в точке М называется число, равное 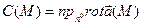 .
.
Определение: Функция 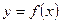 называется непрерывной в точке
называется непрерывной в точке  , если существует предел функции в точке
, если существует предел функции в точке  , равный значению функции в точке
, равный значению функции в точке  , т. е.
, т. е. 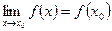 .
.
Определение: Точка  называется точкой разрыва первого рода, если существуют конечные, но неравные односторонние пределы функции в точке
называется точкой разрыва первого рода, если существуют конечные, но неравные односторонние пределы функции в точке  . Разность между правым и левым пределами называется скачком.
. Разность между правым и левым пределами называется скачком.
Определение: Точка  называется точкой разрыва второго рода, если хотя бы один из односторонних пределов равен
называется точкой разрыва второго рода, если хотя бы один из односторонних пределов равен 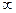 или не существует.
или не существует.
Определение: Точка  называется точкой разрыва устранимого, если существует предел функции в этой точке, не равный значению функции в точке
называется точкой разрыва устранимого, если существует предел функции в этой точке, не равный значению функции в точке  .
.
Определение: Пусть функция 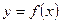 задана на некотором множестве
задана на некотором множестве 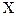 . Зафиксируем значение аргумента
. Зафиксируем значение аргумента 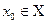 и придадим ему приращение
и придадим ему приращение 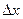 , не выводящее значение аргумента за пределы множества
, не выводящее значение аргумента за пределы множества 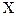 , т. е.
, т. е. 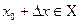 . Тогда соответствующее приращение
. Тогда соответствующее приращение 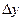 получит и сама функция, которое равно разности нового и старого значений функции.
получит и сама функция, которое равно разности нового и старого значений функции.
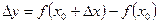 . Если существует предел отношения приращения функции к приращению аргумента, при
. Если существует предел отношения приращения функции к приращению аргумента, при 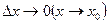 , то он называется производной функции в точке
, то он называется производной функции в точке  . Пишут
. Пишут 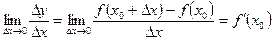 , или
, или 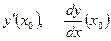 .
.
Определение: Производной второго порядка функции 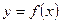 называется производная от первой производной, т. е.
называется производная от первой производной, т. е. 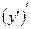 . Обозначают
. Обозначают 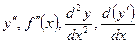 .
.
Определение: Производной n-го порядка функции 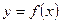 называют производную от производной (n – 1)-го порядка данной функции. Обозначают
называют производную от производной (n – 1)-го порядка данной функции. Обозначают 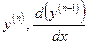 .
.
Приложение 1
Контрольная работа № 1 по теме:
«Элементы векторной алгебры и аналитической геометрии»
Задание № 1.1.Найти: а)  ,
, 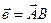 ;
;
б) модуль вектора 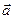 ;
;
в) скалярное произведение ( 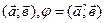 ;
;
г) векторное произведение векторов;
д) смешанное произведение векторов 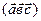 ;
; 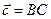 .
.
А В С
1.10 (3,1–2) (–1,6,1) (–1,1,6)
1.11 (3,1,4) (–1,0,1) (1,7,3)
1.12 (3,5,4) (5,8,3) (1,2,–2)
1.13 (2,4,3) (1,1,5) (4,9,3)
1.14 (9,5,5) (–3,7,1) (5,7,8)
1.15 (0,7,1) (2, –1,5) (1,6,3)
1.16 (1,1,2) (1, –1, –1) (3,5,1)
1.17 (6,6,1) (4,6,6) (4,2,0)
1.18 (7,5,3) (9,4,4) (4,5,7)
1.19 (6,8,2) (5,4,7) (2,4,7)
Задание № 1.2.Доказать, что векторы 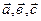 образуют базис, и найти координаты вектора
образуют базис, и найти координаты вектора 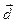 в этом базисе.
в этом базисе.
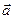 | 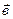 | 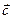 | 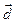 | |
| 1.20 | (2,2,3) | (1,3,2) | (3,1,1) | (7,1,6) |
| 1.21 | (3,1,5) | (–1,2,1) | (1,4,2) | (12,6,3) |
| 1.22 | (2,1,4) | (–1,1,1) | (2,2,4) | (3,–4,–3) |
| 1.23 | (2,1,1) | (–1,3,2) | (3,–1,2) | (–4,11,7) |
| 1.24 | (3,3,2) | (–2,4, –1) | (4,–2,–1) | (12,6,–9) |
| 1.25 | (8,1,4) | (3,1,1) | (–6,–1,–3) | (–4,2,–5) |
| 1.26 | (4,1,8) | (1,1,3) | (–3,–1,–6) | (9,–2,12) |
| 1.27 | (2,7,4) | (3,–5,0) | (4,0,11) | (33,24,39) |
| 1.28 | (2,7,4) | (3,–5,0) | (4,1,1) | (12,–33,–7) |
| 1.29 | (1,0,3) | (4,5,–2) | (–1,4,5) | (6,–20,–22) |
Задание № 1.3.Сила 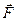 приложена к точке А. Вычислить:
приложена к точке А. Вычислить:
а) работу силы 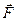 , если точка ее приложения, двигаясь прямолинейно, переместилась в точку В;
, если точка ее приложения, двигаясь прямолинейно, переместилась в точку В;
б) модуль вращающего момента силы 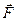 , точки В.
, точки В.
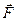 | 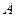 | 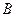 | |
| 1.30 | (1,3,4) | (2,0,–1) | (–3,–1,–2) |
| 1.31 | (1,0,3) | (–2,0,3) | (–2,–1,0) |
| 1.32 | (3,2,1) | (2,3,5) | (–1,0,–3) |
| 1.33 | (2,1,1) | (–1,3,2) | (3,–1,2) |
| 1.34 | (–1,3,5) | (–2,–5,9) | (–1,–6,5) |
| 1.35 | (–1,2,1) | (2,–1,4) | (4,–2,0) |
| 1.36 | (1,–5,0) | (–3,0,7) | (–4,3,4) |
| 1.37 | (2,3,1) | (4,0,2) | (5,–4,1) |
| 1.38 | (0,–1,3) | (2,4,6) | (5,5,0) |
| 1.39 | (3,1,–2) | (0,1,4) | (–3,2,5) |
Задание № 1.4.Заданы три точки пространства А, В и С (координаты точек взять из задания 1.1). Найти:
а) уравнение стороны АВ треугольника АВС;
б) периметр треугольника (до 0,01);
в) уравнение плоскости (АВС);
г) площадь треугольника (до 0,01).
Задание № 1.5.Проверить совместность системы линейных алгебраических уравнений и решить ее:
а) методом Крамера;
б) методом Гаусса;
в) матричным методом.
1.50 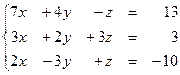 1.51
1.51 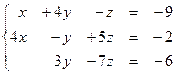
1.52 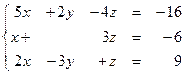 1.53
1.53 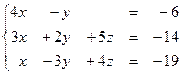
1.54 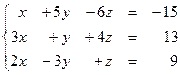 1.55
1.55 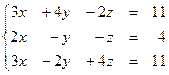
1.56 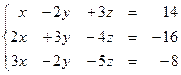 1.57
1.57 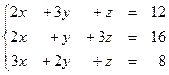
1.58 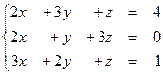 1.59
1.59 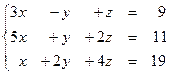
Приложение 2
