Аналитические выражения для характеристик гранулометрического состава горной массы

Эмпирические исследования крупности дробленого материала дали к настоящему времени целую систему весьма похожих анали­тических выражений, описывающих гранулометрический состав дроб­леных или измельченных горных пород, полученных на различных стадиях процесса обогащения. Необходимо отметить, что этот опыт заимствован в основном из работ обогатителей, которые первыми заинтересовались этой проблемой.

Все приведенные ниже аналитические зависимости представля­ют собой аппроксимации данных по реальным совокупностям частиц или кусков дробленых пород, полученных методами ситового (в основном) анализа.

Более чем столетняя история применения этого метода выработала приемы, позволяющие уверенно судить о достоверности и точности данных гранулометрического анализа.

Среди этих попыток аппроксимации можно указать, например, формулу Роллера

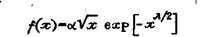(9)

для описания распределения размеров дробленых материалов.

К этому же типу зависимостей относится формула Нукиямы -Тонасавн

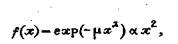(10)

описывающая крупность пыльных частиц, полученных при дроблении в широком диапазоне размеров.

Для описания распределения частиц горной массы в дробилках и мельницах можно использовать формулу Годена - Андреева

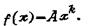(11)

Наиболее распространено эмпирическое соотношение Розина -Раммлера

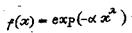. - (12)

Если формулы (9) и (10) получили в свое время распространение при описании крупности мелких пылевидных частиц, то формула (12) универсальна и описывает крупность кусков горной массы при взрыве дроблении в дробилках, измельчении в мельницах, а также годится для описания дисперсного состава пылевых частиц.

В формулах (9)-(12) f(x)- доля частиц размером х в общем количестве частиц; А , μ, λ, α, κ- постоянные параметры, зависящие от характеристик и крупности дробленого материала. Эти параметры определяют экспериментально по данным замеров кусковатости для каждого конкретного случая.

Особое внимание привлекают к себе те аппроксимационные соотношения, которые образуются из известных статистических распределений. К ним относятся прежде всего логарифмически-нормальное и нормальное распределения, гамма-распределение и как вариант Г -распределения - распределение Вейбулла, а также другие виды усложненных распределений или их комбинации. Первые попытки использовать стандартные типы распределе­ний к описанию распределения крупности дробленого материала привели к выводу о практической неприменимости нормального закона ввиду существенной асимметрии таких распределений.

Хорошие результаты аппроксимации в широком диапазоне размеров кусков были получены с использованием логарифмически нормального закона распределения

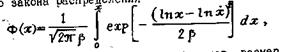(13)

где Ф(x)- суммарный выход снизу - доля кусков, размер которых меньше х ; β - логарифмическая дисперсия,

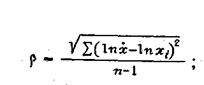(14)

х - средний геометрический размер куска

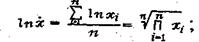(15)

п - число кусков; xi - размеры кусков.

Основные параметры этого распределения: средний геометрический размер и логарифмическая дисперсия, - разброс логарифма размеров - имеют четкий физический смысл статистических параметров, точность определения которых и надежность оценки проверяются отработанными и хороша известными статистическими методами. Среднее геометрическое - центр распределения - характеризует медианный размер, разделяющий все распределение на две равные части - больше его и меньше. Логарифмическая дисперсия - мера разброса значений размеров относительно среднего.

Путем несложных преобразований координат; выполненных на основе табулиро­ванных функций распределения вероятностей (интеграл Гаусса)

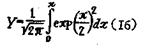
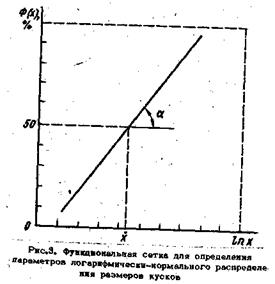
и логарифмического преобразования, графическое выражение логарифмически-нормального закона сводится к прямой линии, проходящей через точку с параметрами (lnx; 50) под углом, котангенс которого равен β- логарифмической дисперсии (рис.3).

Суммарные проценты по данным гранулометрического анализа можно наносить на график (рис.3) и в том случае, если данные аппроксимируются по логарифмически-нормальному закону распределения. Тогда экспериментальные точки выравниваются прямой линией в координатах (lnx; Ф(х))Такой способ представления данных позволяет графически надежно и с большой точностью определить параметры аналитической зависимости.

Еще один пример аналитического описания распределения размеров кусков связан с использованием известного статистического распределения Вейбулла____

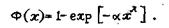
Сопоставляя формулы (12) и (17) легко видеть, что закон Розина - Раммлера легко сводится к распределению Вейбулла, в связи с чем можно пользоваться общими приемами при построении этих распределений.

Характеристики закона распределения Вейбулла следующие: интегральная (по минимуму) функция распределения

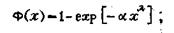(17)

плотность распределения

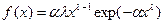(18)

математическое ожидание (средний кусок)

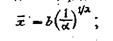(19)

дисперсия

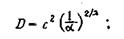(20)

среднеквадратическое отклонение

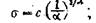(21)

коэффициент вариации

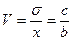(22)

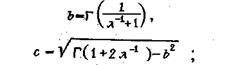где α и λ - определяющие параметры формы и масштаба соответственно; b и с - вспомогательные величины,

(23) (24)

Г - гамма-функция.

Определяющие параметры этого распределения связаны, как следует из формулы (19), соотношением

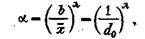(25)

где b - размер отверстия сита, через которое прошло 63,2 % разрушенного материала; d₀- средний размер, Тогда функция распределения

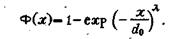(26)

Значения определяющих параметров α и λ в формуле (17) можно находить по следующей схеме:

1) по экспериментальным данным определяют средний кусок, дисперсию и коэффициент вариации;

2) по величине коэффициента вариации находят с помощью вспомогательной таблицы (табл.2) значения параметра λ л и вспомогательных величин bи с;

3) исходя из экспериментальной оценки среднеквадратического отклонения и найденных значений b и с, определяют параметр масштаба α;

4) для конкретных размеров проводят расчет функции распределения по формулам (17)-(26).

Таблица 2

Вспомогательная таблица для расчета параметров распределения Вейбулла

Коэффициент вариации	Параметр формы	Вспомогательные величины
νвар	λ	1/λ	1/λ2	b	С
3,140	0,400	2,500	6.250	" 3,320	10,400
2,930	0,417	2,400	5,760	2,980	8,740
2,750	0,435	2,300	5,290	2,680	7,880
2,570	0,455	2,200	4,840	2,420	6,220
2,400	0,476	2,100	4,410	2,200	5,270
2,240	0,500	2,000	4,000	2,000	4,470
2,080	0,526	1,900	3,610	1,830 ;	8,810
1,940	0,556	1,800	3,240	1,680	8,260
1,800	0,588	1,700	2,890	1,540	2,780
1,670	0,625	1,600	2,560	1,430	2,390
1,550	0,667	1,500	2,250	1,330	2,060
1,430	0,714	1,400	1,960	" 1,240	1,780
1,320	0,769	1,300	1,690	1,170	1.540
1,210	0,833.	1,200	1,450	1,100	1.330
1,100	0,909	1,100	1,210	1,050	1,150
1,000	1,000	1,000	1,100	1,000 .	1,000
0,910	1,100	0,909

Подобный расчет аналитической функции распределения громоздок и неудобен. Проще и эффективнее использовать графический способ расчета параметров распределения Вейбулла. Из экспериментально полученного графика можно определить непосредственно параметры α и λследующим образом.

Координатная сетка в координатах 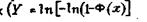и 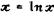) строится на, основе .линейного уравнения

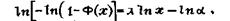(27)

преобразованного из уравнения (17) двойным логарифмированием.

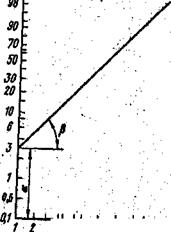
Суммарная характеристика кусковатости дробленого материала должна выравниваться в этих координатах в прямую линию с угловым параметром λ=ctgβи начальным - масштабным параметром α. Начало координат в логарифмической шкале по осиабсцисс начинается от единицы (рис.4). Выравнивание экспериментальных данных на координатной сетке можно проводить методом наименьших квадратов, определяя при этом сразу параметры α и λ:

Рио.4. Схема определения параметров распределения Вейбулла

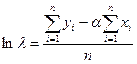(28)

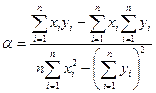(29)

где n - количество экспериментальных точек; x_i-и у_i- - координаты экспериментальных точек в принятой системе координат^-.

В работах В.Н.Кузнецова предполагается использовать для аппроксимации распределения размеров кусков гамма-распределение. Объемы кусков горной массы с точностью 5% распределены по размерам в соответствии с неполной гамма-функцией типа

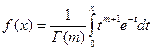(30)

Где 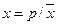; 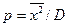D - дисперсия распределения; х - математическое ожидание размеров куска (средний размер куска); Г - гамма-функция; т - параметр формы; т=р+3; t - переменная интегрирования.

Соотношение между средним размером и дисперсией большинства природных материалов x²/D~3. Тогда в формуле (30) один параметр исключается и функция f(x) получает вид

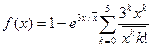(31)

Наряду с известными законами распределения для описания кусковатости дробленого материала применялись различные их модификации которые помогали с большей точностью описать особенности реальных распределений размеров кусков. Так, например, В.А.Безматерных указывал, что разрушенные взрывом цилиндрические образцы пород имеют двухмодальное распределение (распределение с двумя максимумами). В этом случае любые из перечисленных выше аппроксимаций будут малоэффективными.

Логарифмически-нормальная аппроксимация кусковатости горной массы корректна только в ограниченном диапазоне размеров. Асимптотической части теоретического распределения размеров, больше или меньше некоторых предельных (обычно под этим понимаются размеры кусков, близких к негабаритным), существенно отклонялись от опытных данных, в связи„с чем были введены до­полнительные параметры, учитывающие конечный характер распределения размеров кусков по крайней мере по максимальному размеру. Тогда реальный гранулометрический состав горной массы аппроксимировался усеченным по максимальному размеру логарифмически-нормальным законом распределения, функция распределения которого имеет вид

Ф(х)=Ф(ξ)[1-Ф(х_max)] (32)

где Ф(х) - искомое усеченное логарифмически-нормальное распределение; Ф(ξ)- экспоненциальная аппроксимация (гипотетический полный логарифмически-нормальный закон распределения, экстраполируемый в область крупных размеров кусков); х_тах-максимальный размер куска, замеренный при анализе гранулометрического состава (рис.5).

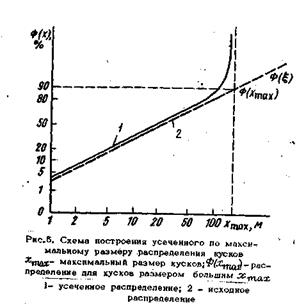Точка Ф (х_тах) определяется пересечением графика Фр с абсциссой. Дальнейший расчет истинного усеченного по максимальному размеру распределения производится по формуле (32).

Такой способ представления данных гранулометрического анализа достаточно эффективен при условии точного определения максимального размера куска в совокупности и малых долей усечения.

При больших долях усечения удобно пользоваться преобразованием случайной величины размера кусков

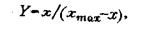(33)

где У - преобразованная случайная величина,

В таком случае величина Y будет распределена логарифмически-нормально в диапазоне значений от 0 до¥. В этом же методическом плане можно исследовать любые части общего распределения кусковатости, например, распределение разменов негабаритных кусков. Тогда преобразованная случайная величина будет характеризоваться не только максимальным, но и минимальным размером:

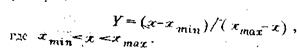(34)

Распределение этой случайной величины будет линейным в логарифмически-вероятностной сетке во всем диапазоне размеров.

Для того, чтобы скорректировать отклонения реальных дан­ных от теоретических зависимостей, записанных в форме логарифмически-нормального распределения Розина - Раммлера, применяют не только дополнительные параметры, связанные с ограниче­нием в области крупных и мелких размеров, но, как показал опыт, вынуждены вводить параметры, учитывающие функциональное изменение дисперсии от размера частиц. Значения логарифмической дисперсии при описании кусковатости материала после дро­билок менялись в зависимости от крупности фракций. Таким образом, число независимых параметров, характеризующих кусковатость горной массы в аналитической форме, доходило до четырех, что существенно ограничивало область применения таких аппроксимаций, для технических целей.

Многообразие форм аналитической записи характеристик кусковатости горной массы свидетельствует прежде всего о сложно­сти процессов, формирующих совокупность кусков, о невозможности систематизировать имеющийся материален исследовательский опыт.

Сложность аналитической записи кусковатости во всем диапазоне размеров может свидетельствовать также о том, что формирование различных фракций обуславливается различными причи­нами. Чем вире диапазон размеров, который следует описать аналитическим выражением, тем сложнее зависимость и больше количество независимых параметров. Это видно уже на примере зависимости Нукиямы - Тонасавы, где гранулометрический состав промышленных пылей, имеющих диапазоны размеров от долей микронов до нескольких миллиметров, описывается зависимостью с четырьмя независимыми параметрами. Примерно такие же условия возникают при описании кусковатости горной массы, когда требуется одной зависимостью описать как негабаритную часть совокупности кусков, так и долю мелочи, в результате чего появляются разного рода дополнения к закону распределения в виде усечения или многомодельности.

Простота аналитических зависимостей, имеющих два параметра, обуславливает широкую применимость основных законов распределения (зависимость Розина - Раммлера, Вейбулла, логарифмически-нормальный), несмотря на ограничения этих аппроксима­ций малым диапазоном размеров. Следует указать, что диапазон размеров кусков, непосредственно и существенно влияющий на технологические параметры экскавации и транспорта горной массы, оценивается примерно одним порядком.

Детальное исследование адекватности того или иного закона распределения для аппроксимации реального гранулометрического состава проводится обычными статистическими методами. Так, например, применимость логарифмически-анормального распределения или закона Розина - Раммлера для описания кусковатоcти оценивалась с помощью критерия g² , причем части совокупности кусков, исследованные одним и тем же способом на близких по физико-механическим свойствам массивах пород, аппроксимировались различными типами распределений с приемлемыми значениями критерия согласия g². Это обстоятельство говорит, во-первых, о малой разнице в ограниченных диапазонах крупности кусков между указанными законами распределения и, во-вторых, о недостаточной точности замеров, позволяющих интерпретировать данные различными способами.

Не вдаваясь в подробности проверки статистических гипотез по материалам экспериментальных данных с неустановленными методическими принципами, обратим внимание на тот факт, что адекватность того или иного аналитического закона распределения необходимо проверять не только статистическими методами, но и соответствием физической гипотезе формирования совокупности кусков горной массы, приводящей к данному типу распределений.

Таким образом, приступая к рассмотрений теоретических моделей процесса разрушения горных пород взрывом, необходимо учитывать многозначность имеющегося экспериментального материала, который может с равным успехом подтверждать правомерность использования различных моделей разрушающего действия взрыва.