Особенность аксиоматического метода
Ни одно математическое высказывание (или свойство), взятое в отдельности, не является аксиомой, так как его всегда можно доказать на основании других высказываний (свойств). Например, в геометрии обычно принимается за аксиому следующее свойство параллельных прямых линий: «Через одну и ту же точку нельзя провести две различные прямые, параллельные одной и той же прямой» (аксиома параллельности). На основании этой аксиомы (и ряда других) доказывается такое свойство треугольника, как: «Сумма углов треугольника равна 180о». Между тем, можно было бы это свойство принять за аксиому вместо аксиомы параллельности (оставив остальные аксиомы прежними). Тогда свойство параллельности прямых линий можно доказать, и оно станет теоремой.
Таким образом, систему аксиом можно выбирать различными способами. Нужно только, чтобы взятых аксиом было достаточно для вывода всех прочих высказываний.
Отметим, что при построении доказательств число аксиом стремятся, по возможности, уменьшить.
Основные методы доказательств.
Метод цепочек импликаций состоит в том, что из посылки А выстраивается цепочка из n импликаций, последним высказыванием в которой является заключение теоремы В, т.е.
.
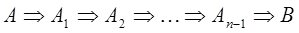В основе этого метода лежит закон цепного высказывания, или закон силлогизма:
.
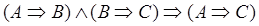Символ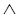 
означает логический союз «и», а выражение 
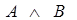читается, как «А и В».
Метод от противного.
Этот метод основан на законе контрапозиций, который имеет вид:
.
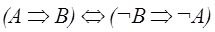Символ (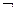 
) соответствует логическому союзу «не»,
выражение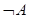 
читается, как: «не А», или «не верно, что А».
Символ (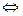 
) соответствует любому из трёх логических высказываний:
1) «необходимо и достаточно»,
2) «тогда и только тогда»
3) «эквивалентно»
Метод необходимого и достаточного.
Например, теорема формулируется так: «Чтобы имело место А, необходимо и достаточно выполнение В».
Доказательство такого вида теоремы распадается на две части: сначала доказывается, что если имеет место А, то справедливо В (В необходимо для А), затем доказывается, что если имеет место В, то имеет место и А (В достаточно для А).
Доказательство таким методом базируется на законе тавтологии:
.
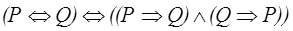Упражнения для самостоятельного анализа к Разделу 1:
Упражнение 1.
Установите правильное соответствие между математическим утверждением и его формулировкой.
| 1. «В любой треугольник можно вписать окружность». | А. Определение B. Аксиома C. Теорема |
| 2. «Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник». | |
| 3. «Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна». |
Упражнение 2.
Выберите правильный ответ. К неопределяемым понятиям аксиоматического построения геометрии на плоскости относятся …
| 1) фигура, плоскость, луч | 2) луч, треугольник, плоскость |
| 3) точка, прямая, плоскость | 4) точка, отрезок, плоскость |
Упражнение 3.
Среди предложенных математических утверждений евклидовой геометрии аксиомой является…
1) Если две параллельные прямые пересечены секущей, то соответственные углы равны.
2) Две прямые, параллельные третьей прямой, параллельны.
3) Две прямые на плоскости называются параллельными, если они не пересекаются.
4) Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Упражнение 4.
Установите правильное соответствие между математическим утверждением и его формулировкой.
| 1. «Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны». | А. Определение B. Аксиома C. Теорема |
| 2. «На каждой прямой и в каждой плоскости имеются, по крайней мере, две точки». | |
| 3. «Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны». |
Упражнение 5.
Среди предложенных математических утверждений аксиомой является…
1) Через любые две точки плоскости можно провести прямую, и притом только одну.
2) В равнобедренном треугольнике углы при основании равны.
3) Диагонали параллелограмма точкой пересечения делятся пополам.
4) Вертикальные углы равны.