Уравнение Бернулли и следствия из него. Истечение жидкости из отверстия

Уравнение Бернулли

Для идеальной жидкости (сила трения полностью отсутствует) справедливо уравнение, которое было получено швейцарским математиком и физиком Даниилом Бернулли (1700-1782). Рассмотрим тонкую трубку тока и выделим в ней два произвольных сечения (рис. 7.2).

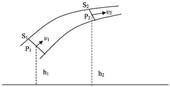Рис. 7.2. Параметры сечений в трубке тока

В общем случае эти сечения находятся на различных высотах (h1 и h2), а их площади различны (S1 и S2). Вследствие уравнения неразрывности различны будут и скорости течения жидкости в этих сечениях (v1 и v2). Обозначим давления жидкости в этих сечениях Р1 и Р2 соответственно.

Используя закон сохранения механической энергии, можно доказать, что для этих сечений выполняется следующее соотношение:

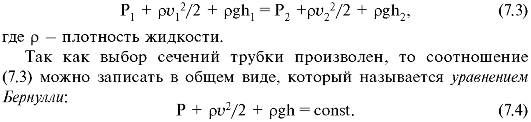Давление Р называют статическим. Это давление, которое оказывают друг на друга соседние слои жидкости. Его можно измерить манометром, который движется вместе с жидкостью. Величину ρv2/2 называют динамическим давлением. Оно обусловлено движением жидкости.Гидростатическое давление ρgh - это давление, создаваемое весом вертикального столба жидкости высотой h.

Уравнение Бернулли формулируется следующим образом:

При стационарном течении идеальной жидкости полное давление, равное сумме статического, динамического и гидростатического давлений, одинаково во всех поперечных сечениях трубки тока.

7.3. Следствия уравнения Бернулли

Горизонтальная трубка тока переменного сечения

При этом h1 = h2 и уравнение (7.3.) принимает вид

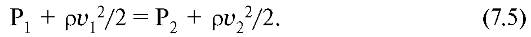Отсюда следует, что статическое давление идеальной жидкости при течении по горизонтальной трубке возрастает там, где скорость ее уменьшается, и наоборот. Это можно продемонстрировать с помощью манометрических трубок, уровень поднятия жидкости в которых пропорционален статическому давлению (рис. 7.3). Видно, что в широком сечении (а), где скорость течения меньше, статическое давление больше, чем в узком сечении (б).

Истечение жидкости из отверстия

Фо́рмула Торриче́лли – связывает скорость истечения жидкости из малого отверстия в открытом сосуде с высотой жидкости над отверстием[1].

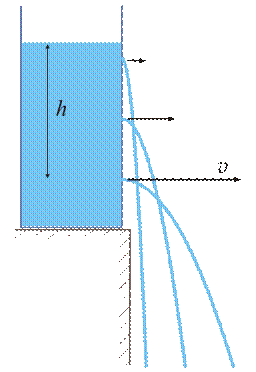
Формула Торричелли утверждает, что скорость 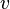истечения жидкости через отверстие в тонкой стенке, находящееся в ёмкости на глубине 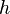от поверхности, такая же, как и у тела, свободно падающего с высоты 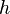, то есть

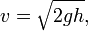
где 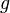– ускорение свободного падения.

Последнее выражение получено в результате приравнивания приобретённой кинетической энергии 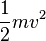и потерянной потенциальной энергии .

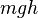Эта формула была получена (хотя и не в приведённой выше форме[2]) итальянским учёным Эванджелиста Торричелли, в 1643 году. Позже было показано, что эта формула является следствием закона Бернулли.