При подготовки к экзамену по разделу «Молекулярная (статистическая) физика и термодинамика»

Молекулярная (статистическая) физика и термодинамика

Программа

Молекулярно-кинетическая теория идеальных газов

Распределение молекул газа по скоростям (Максвелла). Характерные скорости распределения Максвелла: наивероятнейшая, средняя и среднеквадратичная скорости молекул газа. Распределение молекул по компонентам скоростей. Число молекул в различных участках распределения. Частота ударов молекул о стенку. Средняя кинетическая энергия молекул

Столкновения молекул в газе. Длина свободного пробега. Частота соударений.

Молекулярная теория давления идеального газа. Основное уравнение кинетической теории идеальных газов. Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева). Закон Дальтона. Закон Авогадро.

Распределение Больцмана. Барометрическая формула.

Теорема о равномерном распределении кинетической энергии по степеням свободы. Число степеней свободы молекул идеального газа.

Процессы переноса в газах: диффузия, внутреннее трение, теплопроводность.

Диффузия: закон Фика. Внутреннее трение (перенос импульса): закон Ньютона - Стокса. Теплопроводность: закон Фурье. Уравнение переноса.

Связь коэффициентов переноса с молекулярно-кинетическими характеристиками газа. Зависимость коэффициентов переноса от температуры и плотности.

Термодинамика

Квазистатические процессы. Обратимые и необратимые процессы. Понятие функции состояния. Внутренняя энергия. Теплота и работа. Первое начало термодинамики.Теплоемкость идеального газа. Связь теплоемкости газа с числом степеней свободы молекул. Уравнение Майера. Процессы в идеальных газах: изотермический, изохорический, изобарический, адиабатический, политропный процесс. Работа в этих процессах.

Энтропия идеального газа. Расчет изменения энтропии в процессах идеального газа. Зависимость энтропии от давления и объема в изотермических процессах

Циклические процессы.Работа цикла.Коэффициент полезного действия. Цикл Карно.

Термодинамические потенциалы и их характеристические

Переменные

Свободная энергия. Потенциал Гиббса. Энтальпия.

Реальные газы, жидкости и твердые тела

Изотермы, уравнение Ван-дер-Ваальса. Внутренняя энергия реального газа. Адиабатическое расширение реального газа в пустоту. Свободная поверхностная энергия. Поверхностное натяжение. Краевой угол смачивания. Давление под искривленной поверхностью жидкости. Капиллярные явления. Теплоемкость твердого тела.

Фазовые переходы первого и второго рода. Уравнение Клапейрона-Клаузиуса. Скрытая теплота перехода. Диаграммы состояний.

Вопросы и задания для самостоятельной работы студентов

при подготовки к экзамену по разделу «Молекулярная (статистическая) физика и термодинамика»

1. Каков физический смысл функции распределения молекул по скоростям?

2. Как изменяется распределение Максвелла с ростом температуры?

3. Чем обуславливается существование максимума на кривой, характеризующей распределение Максвелла?

4. Запишите функции распределения Максвелла 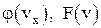, что они характеризуют?

5. Как определяются значения наиболее вероятной, среднеарифметической и среднеквадратичной скоростей.

6. Изобразите вид кривой распределения 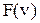и отметьте примерные положения наиболее вероятной, среднеарифметической и среднеквадратичной скоростей.

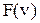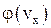7. Изобразите примерные графики функции и для двух разных значений температур.

8. Изобразите примерные графики функции 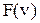для двух газов с различными значениями молярной массы.

9. По графику определите долю молекул газа при температуре Т, обладающих скоростями, лежащими в интервале от v до v + dv?

10. По графику определите долю молекул газа при температуре 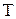, скорости которых больше некоторого заданного значения ?

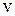11. Запишите формулу для среднего числа столкновений молекул в газе.

12. Что такое средняя длина свободного пробега молекул газа? Вcпомните формулу для средней длины свободного пробега молекул.

13. Получите численное значение средней длины свободного пробега для молекул газа, находящегося при нормальных условиях.

14. Что называется числом степеней свободы?

15. Каким числом переменных можно описать состояние двухатомной молекулы? Что характеризуют эти переменные?

16. Какая энергия приходится на поступательную степень свободы? Вращательную? Колебательную?

17. Полагая, что число атомов в молекуле равно N, определите среднюю энергию одной молекулы (линейной, нелинейной).

18. Запишите основное уравнение молекулярно-кинетической теории.

19. Что Вы понимаете под уравнением состояния системы? Запишите уравнение состояния для идеального газа.

20. Что характеризует число Авогадро?

21. В чем сущность закона Дальтона?

22. В чем сущность закона Авогадро?

23. Какой смысл получает параметр температуры при молекулярно-кинетическом исследовании тепловых свойств вещества?

24. Запишите закон распределения Больцмана. Объясните его сущность.

25. Как определить концентрацию молекул равновесного газа, находящегося при температуре Т во внешнем потенциальном поле?

26. Запишите барометрическую формулу и рассмотрите изменение давления с высотой для различных газов.

27. Объясните процесс диффузии (вязкости, теплопроводности). В чем состоит сущность этих процессов с точки зрения молекулярно-кинетической теории?

28. Приведите экспериментальные законы, описывающие явления переноса.

29. Вспомните формулы для коэффициентов переноса.

30. Как зависят коэффициенты переноса от температуры и давления?

31. Что такое внутренняя энергия идеального газа. Какими параметрами она определяется?

32. В результате каких процессов может измениться внутренняя энергия системы?

33. Дайте понятие количества теплоты, работы. Как определяются эти величины? Как работа определяется графически на диаграмме p, V?

34. В чем состоит содержание первого начала термодинамики? Как математически записывается этот закон?

35. Запишите выражение для внутренней энергии одного моля идеального газа.

36. Что называется теплоемкостью, удельной и молярной теплоемкостями?

37. Как математически связаны теплоемкост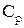и и 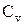(уравнение Майера)?

38. Какие термодинамические процессы Вам известны, и какими уравнениями они описываются? Изобразите графики этих процессов. Получите выражения для работы, совершаемой системой при этих процессах.

39. В каких случаях приращение внутренней энергии системы равно подведенному к системе количеству тепла?

40. В каких случаях внутренняя энергия системы постоянна?

41. В каких случаях изменение внутренней энергии системы равно внешней работе, совершенной системой?

42. Запишите уравнение адиабатического процесса и найдите работу, выполненную системой при этом процессе.

43. Как изменяется температура газа при адиабатическом сжатии? Расширении?

44. Запишите уравнение политропического процесса.

45. Опишите цикл Карно с идеальным газом. Приведите формулу для КПД цикла Карно.

46. Сформулируйте теоремы Карно.

47. Дайте понятие энтропии.

48. Получите математическое выражение энтропии для различных процессов.

49. Как зависит энтропия от давления и объема в изотермических процессах?

50. Изобразите в системе координат T, S изотермический и адиабатический процессы.

51. Запишите основное уравнение термодинамики, связывающее первое начало со вторым.

52. Изобразите цикл Карно на диаграмме S, T (S – энтропия, T – температура) и найдите выражение для КПД цикла.

53. Получите формулу для приращения энтропии идеального газа, если его параметры изменяются в пределах от Р₁ до Р₂ и от V₁ до V₂.

54. Запишите уравнение состояния реального газа для одного моля и произвольного количества вещества.

55. От каких параметров зависит внутренняя энергия газа Ван-дер-Ваальса?

56. При адиабатическом расширении газа в пустоту его внутренняя энергия не меняется. Как изменяется температура, если газ идеальный? реальный?

57. Изобразите экспериментальные изотермы реального газа. Опишите зависимость давления насыщенных паров от температуры.

58. Что такое критическое состояние вещества? Критическая температура?

59. Можно ли газ перевести в жидкое состояние, используя высокое давление, или для сжижения газа необходимо создавать специальные условия?

60. Объясните механизм возникновения сил поверхностного натяжения. Покажите, что коэффициент поверхностного натяжения определяется работой, которую нужно затратить, чтобы увеличить поверхность пленки на единицу площади.

61. Запишите формулу поверхностного молекулярного давления на каплю жидкости радиуса R. Какой вид примет эта формула в случае пузырька того же радиуса?

62. Запишите формулу Лапласа в общем виде.

63. Получите формулу для высоты поднятия (опускания) уровня жидкости в открытой капиллярной трубке.

64. Дайте понятие краевого угла. При каких условиях жидкость смачивает твердое тело? Не смачивает?

65. Как определяется теплоемкость твердых тел по классической теории теплоемкости (закон Дюлонга и Пти)?

66. Определение теплоемкости по квантовой теории? Укажите граничные условия определения теплоемкости по классической и квантовой теории.

67. Считая, что на каждый колеблющийся ион кристаллической решетки приходится один свободный электрон и что, свободные электроны можно рассматривать как идеальный газ, определите атомную теплоемкость кристалла. Сравните полученное значение с выражением закона Дюлонга - Пти. Объясните полученный результат.

68. Чем отличается фазовый переход 1 рода от фазового перехода 2 рода?

69. Какой критерий термодинамического потенциала Гиббса используется при разделении фазовых переходов первого и второго рода?

70. Что такое насыщенный пар? Запишите уравнение зависимости давления насыщенного пара от температуры (уравнение Клапейрона-Клаузиуса).

71. Рассмотрите диаграмму состояния любого вещества. Что можно «вычитать из диаграммы состояния, используемой для изображения фазовых превращений?

Что понимают под скрытой теплотой парообразования (плавления, сублимации)?

Примеры задач

1)) На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 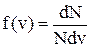– доля молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала.

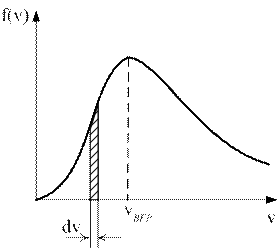
Какие из этих утверждений верны? Дайте обоснованный ответ.

1) Площадь заштрихованной полоски равна доле молекул со скоростями в интервале от v до v+dv.

2) С ростом температуры максимум кривой смещается вправо.

3) С ростом температуры площадь под кривой растет.

2)) На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 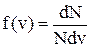– доля молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала.

Какие из этих утверждений верны? Дайте обоснованный ответ.

1) Площадь заштрихованной полоски равна доле молекул со скоростями в интервале от v до v+dv.

2) При понижении температуры максимум кривой смещается влево.

3) При понижении температуры площадь под кривой уменьшается.

3)) На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 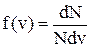– доля молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала.

Какие из этих утверждений верны? Дайте обоснованный ответ.

1) С ростом температуры максимум кривой смещается вправо.

2) С ростом температуры площадь кривой не изменяется.

3) Вид функции распределения не зависит от природы газа (от массы молекул).

4)) На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 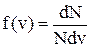– доля молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала.

Какие из этих утверждений верны? Дайте обоснованный ответ.

1) Положение максимума кривой зависит как от температуры, так и от природы газа.

2) При понижении температуры максимум кривой смещается влево.

3) При понижении температуры площадь под кривой уменьшается.

5)) На рисунке схематически представлена температурная зависимость молярной теплоемкости при постоянном объеме C_V от температуры T для двухатомного газа. На участке 2-2’ молекула ведет себя как система, обладающая …(выберите и обоснуйте верный ответ).

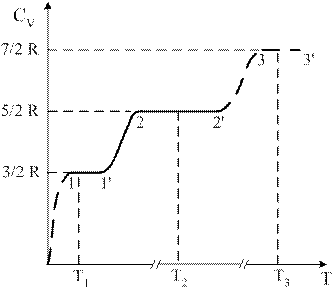
1) тремя поступательными и двумя вращательными степенями свободы

2) только тремя поступательными степенями свободы

3) тремя поступательными, двумя вращательными и колебательной степенями свободы

6)) На рисунке показана зависимость теплоемкости некоторого газа при постоянном объеме от температуры. Выберите и обоснуйте верный ответ.

1). Водород (Н₂); 2). Гелий (Не); 3). Метан (СН₄); 4). Пары воды (Н₂О)

7)) На рисунке изображен цикл Карно в координатах (T,S), где S-энтропия. Изотермическое расширение происходит на этапе …(выберите и обоснуйте правильный ответ).

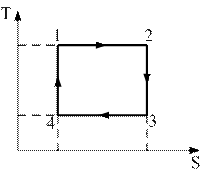
1) 1 – 2

2) 2 – 3

3) 3 – 4

4) 4 – 1

8)) Процесс, изображенный на рисунке в координатах (T,S), где S-энтропия, является…(выберите и обоснуйте правильный ответ).

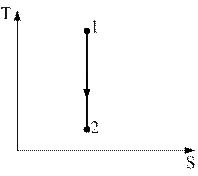
1) адиабатным расширением

2) изохорным охлаждением

3) изобарным сжатием

4) изотермическим сжатием

9)) Каково изменение энтропии ΔS идеального газа при его адиабатическом расширении в пустоту от объема V₁ до объема V₂ ? Выберите верный ответ и обоснуйте его.

1) ΔS = 0; 2) ΔS = R·ln(V₂/V₁); 3) ΔS = R·ln(V₁/V₂); 4) ΔS = R·V₂/V₁ .

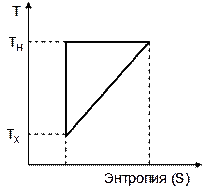10)) Каков КПД тепловой машины, работающей по циклу, изображенному на рисунке. Выберите правильный ответ и обоснуйте его.

1) (Т_Н –Т_Х)/Т_Н ; 2) (Т_Н –Т_Х)/Т_Х ; 3) (Т_Н –Т_Х)/2Т_Н ; 4) (Т_Н –Т_Х)/2Т_Х .

11)) Термодинамический потенциал, приращение которого в равновесном процессе при постоянном давлении дает количество теплоты, полученной системой … (выберите правильный ответ и обоснуйте его).

1). Энтропия; 2). Энтальпия; 3). Свободная энергия; 4). Термодинамический потенциал Гиббса.

12)) На рисунке изображена изотерма пара воды, подвергающегося конденсации. В какой из точек этой изотермы масса жидкости в два раза больше массы пара? Выберите правильный ответ и обоснуйте его.

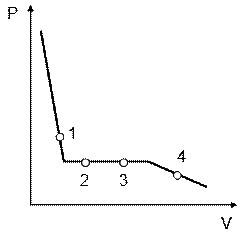1). Точка 1; 2). Точка 1; 3). Точка 3; 4). Точка 4.

13)) N молекул идеального газа находятся в некотором сосуде. Разделим мысленно сосуд на две одинаковые половины А и В. Найти вероятность того, что в половине А сосуда окажется n молекул. Рассмотреть случаи, когда N=5 и n=0,1,2,3,4,5. №2.166

14)) Найти число атомов в молекуле газа, у которого при «замораживании» колебательных степеней свободы постоянная 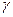увеличивается в 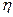=1,20 раза.

15)) Температура гелия (молярная масса 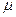=4г/моль), распределение молекул которого по скоростям можно считать максвелловским, изменилась от Т₁=200К до Т₂=400К. Число молекул, скорости которых лежат в узком интервале скоростей от V до 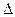V+ V , осталось прежним. Определить скорость этих молекул.

16)) Идеальный газ (гелий), имеющий температуру Т, находится внутри цилиндра высоты Н и радиуса r₀. Газ вместе с цилиндром вращается вокруг оси цилиндра с угловой скоростью 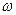. Во сколько раз концентрация молекул у стенок цилиндра превосходит их концентрацию на расстоянии r=r₀/2 от оси цилиндра?

17)) Сосуд, содержащий одноатомный идеальный газ (молярная масса 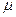=4г/моль), движется со скоростью U=100 км/час. Оценить насколько возрастут средний квадрат скорости теплового движения атомов и температура газа при остановке сосуда. Теплоемкостью и теплопроводностью стенок сосуда можно пренебречь.

18))) Один конец стержня, заключенного в теплоизолирующую оболочку, поддерживается при температуре Т₁, а другой конец - при температуре Т_2. Сам стержень состоит из двух частей, длины которых 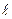₁ и 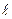₂ и теплопроводност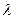и ₁ и 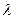₂. Найти температуру поверхности соприкосновения этих частей стержня.

19))) В сосуде при комнатной температуре находится смесь идеальных газов: m1=4кг одноатомного неона и m₂=1кг двухатомного водорода. Определить удельную теплоемкость смеси в изохорическом процессе С_vm. Молярные массы неона и водорода равны, соответственно, 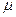₁=20 г/моль, 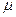₂=2 г/моль.

20)) Квазистатическое расширение идеального газа происходит по закону V=аР^-1/2, где а=const. Определить молярную теплоемкость газа в этом процессе, если его молярная теплоемкость при изохорическом процессе известна и равна С_v.

21))) Оценить изменение температуры плавления льда 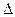Т при повышении давления на 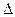Р=1атм. В исходном состоянии (Р=1атм., t=0ºC) известны: удельная теплота плавления льда L=335 Дж/г, удельный объем льда v₂=1,091 см³/г, удельный объем воды v₁=1,000 см³/г.

22)) Найти показатель политропы n процесса, совершаемого идеальным газом, при котором остается неизменным:

а) коэффициент диффузии; б) вязкость; в) теплопроводность.

23)) Вычислить приращение свободной энергии поверхностного слоя при изотермическом слиянии двух одинаковых капель ртути, каждая диаметра d=1,5мм.

24))) Идеальный газ с молярной массой 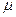находится в однородном поле тяжести, ускорение свободного падения в котором равно g. Найти давление газа как функцию высоты h, если при h=0 давление p=p₀, а температура изменяется с высотой как Т=Т₀(1-аh), где а - положительная постоянная.

25)) Какое количество тепла надо сообщить ν = 3,0 молям углекислого газа, чтобы при расширении в вакуум от объема V₁ = 5,0 л до V₂ = 10 л температура его не изменилась? Газ считать ван-дер-ваальсовским.

26)))Найти уравнение процесса (в переменных Т, V), при котором молярная теплоемкость газа изменяется по закону 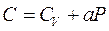, где а = const.

27))) Свободная энергия 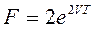. Найти S и P.

28))) Потенциал Гиббса 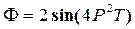. Найти S и V.

29))) Энтальпия 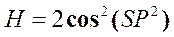. Найти Т и V.

30))) До какой температуры необходимо изобарно нагреть 700 г азота, находящегося при температуре 291 К, чтобы работа расширения газа оказалась равной 41,5 кДж?

31))) В вертикально расположенном цилиндре под поршнем находится газ объемом 2 л при температуре 299 K. Найти работу расширения газа при нагревании его на 100 K. Масса поршня 10 кг, его площадь 50 см², атмосферное давление нормальное.

32))) В вертикальном цилиндре под поршнем находится газ объемом 200 см³ при температуре 350 K. Масса поршня 30 кг, площадь основания 100 см². Газ нагрели на 100 K, сообщив ему 50 кДж теплоты. Найти изменение внутренней энергии газа. Трением поршня о стенки сосуда пренебречь. Атмосферное давление нормальное.

33)) 5 моль идеального газа нагревают на 10 К так, что температура газа меняется пропорционально квадрату объема газа. Какую работу совершает газ при нагревании?

34)) В осях V (объем), p (давление) график процесса в идеальном одноатомном газе имеет вид прямой, соединяющей точки (0,8 л; 100 кПа) и (1 л; 80 кПа). Определите максимальное значение внутренней энергии газа в ходе процесса. Масса газа постоянна.

35)) В цилиндре под поршнем площадью 1 дм² находится один моль воздуха. К поршню через блок привешен груз массой 55 кг. Цилиндр охлаждают на 100 K. На какую высоту поднимется груз? Масса поршня 5 кг. Атмосферное давление нормальное.

)В вертикальном герметически закрытом цилиндре поршень массы т может двигаться без трения. Первоначально давление газа над поршнем равно Р_о, а поршень находится в равновесии. В поршне на короткое время открывают клапан, после установления равновесия поршень опускается вниз на h при прежней температуре. Каково теперь давление газа над поршнем, если общий объём газа выше и ниже поршня равен F?Ускорение свободного падения g.
Решение:

Из уравнений состояния для общего числа молей в начале описываемого процесса имеем: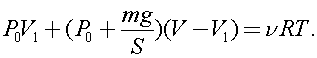

где V₁ - объем газа под поршнем.

После проведенной операции, учитывая опускание поршня, а следовательно уменьшение объема газа под поршнем и увеличение над поршнем можно записать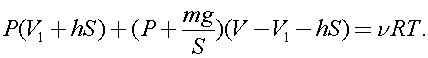
Откуда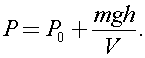
Ответ: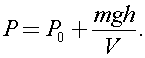

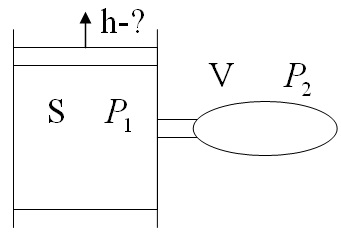2)В цилиндре сечения S под поршнем находится газ при давлении P₁. В баллоне объёма V находится газ при той же температуре и давлении Р₂. После открытия соединительной трубки газ из баллона начинает переходить в цилиндр. Насколько поднимется поршень к моменту установления равновесия и возвращению температуры к исходной?
Решение:

Так как давление над поршнем не меняется, то окончательное давление под поршнем равно Р₁. Газ из баллона расширился до объема 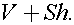Так как процесс происходит при неизменной температуре, то 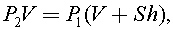отсюда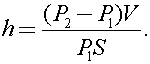
Ответ: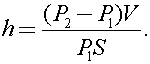

3)Фильтр при пропускании через него воды поглощает 10% содержащихся в ней примесей. Сколько нужно фильтров, чтобы последовательно пропуская через них воду, уменьшить ее менее чем вдвое содержание примесей?
Решение:

1 фильтр уменьшает содержание примесей до 0,9 начального, 2 фильтра до (0,9)² = 0,81 начального, 4 фильтра до (0,9)⁴ = 0,6561, 6 фильтров до (0,9)⁶ = 0,5314, наконец 7 фильтров до (0,9)⁷ =0,4783 Ответ: 7 фильтров.

4)От сосуда отходит вертикальная трубка сечения S. перекрытая столбиком ртути. При повышении температуры газа в сосуде от значения Т₀ до Т столбик ртути в трубке поднялся на h. Определите объём сосуда, если вначале нижняя граница столбика ртути находилась на высоте Н от отверстия в сосуде. Атмосферное давление неизменно.
Решение:

Процесс, описанный в задаче является изобарным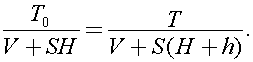

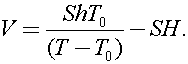
Ответ: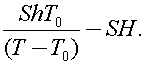

5)Водород хорошо проникает и удерживается в глубине металлического палладия. При нагреве закрытого сосуда объёма V с кусочком палладия внутри от температуры Т₀ до Т давление возросло от Р_о до Р.Найдите массу водорода, выделившегося из кусочка.
Решение:

Считая, что в данных условиях газ в сосуде, как и водород можно считать идеальным, согласно уравнению состояния идеального газа, имеем для начального состояния: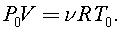

Для конечного состояния: 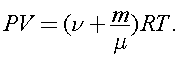Решая совместно эти уравнения, получаем: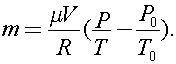

Ответ: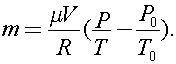

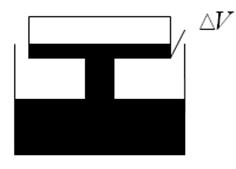6)Колба объемом V = 300 см³, закрытая пробкой с краном, содержит разреженный воздух. Для измерения давления в колбе горлышко колбыпогрузили в воду на незначительную глубину и открыли кран, в результате чего в колбу вошла вода массой m = 292 г. Определить первоначальное давление Р₁ в колбе, если атмосферное давление Р_о =100 кПа.
Решение:

Так как температура воздуха и его масса в колбе не меняется в начале и в конце процесса, то имеет место уравнение: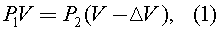
где по закону Паскаля: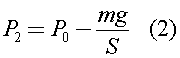

S - средняя площадь поперечного сечения колбы, которую можно оценить по формуле: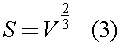

Из данных задачи ясно, что 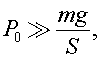поэтому уравнение (1) с учетом (2) и (3) можно записать в виде: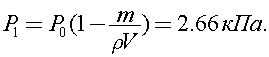
Ответ: 2,66 кПа.

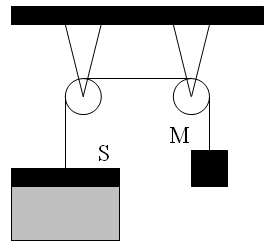7)В цилиндре под невесомым поршнем площадью S = 100 см² находится 1 моль идеального газа при температуре t₁ = 100 °С. К поршню через два блока на невесомой нерастяжимой нити подвешен груз массой М = 17 кг. На какую высоту Δh поднимется груз, если медленно охладить газ до температуры t₂ = 0 °С ? Атмосферное давление Р_о = 10⁵ Па,универсальная газовая постоянная R = 8,31 Дж/(моль∙К), ускорение свободного падения принять g = 10 м/с². Трением пренебречь.
Решение:

Давление газа под поршнем определяется действием двух сил: силы натяжения нити и силы атмосферного давления: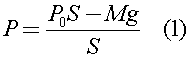

В (1) учтено, что сила натяжения нити Т уравновешивает силу тяжести груза Mg.

Таким образом, из (1) следует, что газ под поршнем будет изобарно расширяться. Тогда из уравнения Клапейрона - Менделеева следует: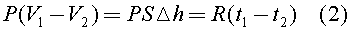
Подставляя (1) в (2), получим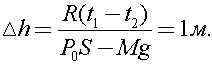
Ответ: 1м.

8) «Ледяной» водой из холодильника заполнили электрический чайник так, что льдинки в него не попали. Чайник сразу включили и вода начала кипеть через время t₁ = 6 минут. Если чайник заполнить таким же объёмом воды при комнатной температуре, он за­кипает за время t₂ = 4,5минуты. Оцените, чему равна комнатная температура T в градусах Цельсия, если выключенный чайник остывает очень долго, а в почти пустом чайнике вола начинает кипеть почти сразу.
Решение:

Долгое остывание говорит о хорошей теплоизоляции. Тогда все поступившее тепло идёт на повышение температуры воды и чайника.Раз в почти пустом чайнике вода закипает почти сразу, то его теплоемкость мала и ею можно пренебречь по сравнению с теплоёмкостью воды в наполненном чайнике.В таком случае уравнение теплового баланса при постоянной мощности: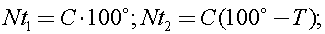

ведь температура «ледяной» воды 0°, а кипящей 100°С.

Отсюда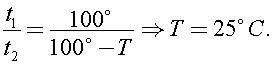
Ответ: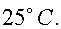

9)В калориметр с горячим чаем бросили кубик льда, имеющий температуру 0 ⁰С. К моменту установления теплового равновесия температура чая понизилась на Δt₁ = 12 ⁰С. Когда в калориметр бросили другой такой же кубик льда, температура чая понизилась еще на Δt₂ = 10 ⁰С. Найдите массу кубика льда. Первоначальная масса чая М = 100 г. Теплоемкостью калориметра, теплообменом с окружающей средой и примесями заварки в чае пренебречь.
Решение:

Запишем уравнение теплового баланса для первого случая: 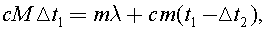где m - масса кубика льда, λ - удельная теплота плавления льда,с - удельная теплоемкость воды, t₁ - исходная температура чая.

Отсюда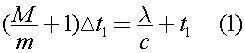

В случае бросания в чай второго кубика мы можем записать уравнение, аналогичное уравнению (1): 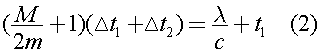Исключая из (1) и (2) правые части, получим: 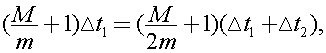откуда легко найти отношение масс: 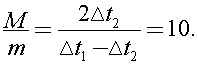Следовательно m =10 г.

Ответ: 10г.

10)В цилиндрическое ведро диаметром d = 20 см налита вода, занимающая объем V = 12,56 л. Каково давление p на стенку ведра на высоте h = 10 см от дна? Атмосферное давление р₀ = 1×10⁵ Н/м².
Решение:

Найдем до какой высоты налита вода в ведре: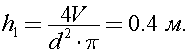

Высота от поверхности воды, на которой необходимо найти давление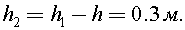
С учетом атмосферного давления гидростатическое давление равно: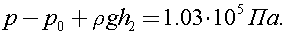
Ответ: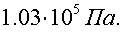

11)Оцените массу земной атмосферы, если давление атмосферы р = 10⁵ Па. Ответ представьте в единицах СИ и округлите до первой значащей цифры.
Решение:
Давление, оказываемое атмосферой на поверхность Земли, равно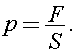
где сила давления равна силе тяжести атмосферы: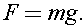
а площадь опоры равна площади земной поверхности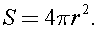
Тогда масса атмосферы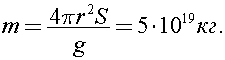
Ответ: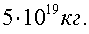

12)В сосуде находится озон О₃ при температуре t₁ = 527 °С. Через некоторое время он полностью превратился в кислород О₂, а температура в сосуде упала до t₂ = 127 °С. На сколько процентов изменилось при этом давление газа? Молярная масса озона M₁, кислорода - M₂.
Решение:

Согласно уравнению Клапейрона - Менделеева для озона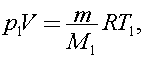

для кислорода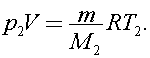

Поделим первое уравнение на второе получим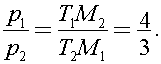

Найдем на сколько процентов изменилось давление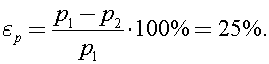
Ответ: 25%

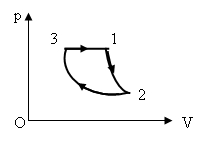13)Один моль гелия совершает цикл, изобра­жен­ный на p-V диаграмме (см. рис.). Участок 1-2 – адиабата, 2-3 – изотерма, 3-1 – изобара. Работа А, совершенная газом за цикл, равна 4 кДж. Разность температур |DТ| газа между состояни­ями 1 и 2 равна 120 К. Какая работа A₂₃ совершается газом в изотер­мическом процессе? Ответ представьте в килоджоулях и округлите до десятых.
Решение:

Из геометрического смысла работы в термодинамике имеем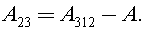
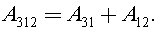
Процесс 3–1 изобарный, тогда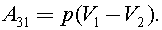

C учетом уравнения Клапейрона - Менделеева, получим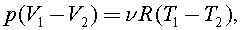

Так как 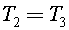то 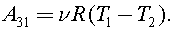Процесс 1–2 адиабатный, тогда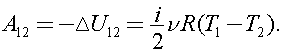

Значит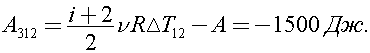
Ответ: -1500 Дж.

14)При температуре t = 17 °С относительная влажность j воздуха в аудитории объемом V = 100 м³ равна80%. Плотность r_н насыщенных паров при данной температуре равна 0,015 кг/м³. Определите массу mпаров воды в аудитории. Ответ представьте в единицах СИ.
Решение:
Относительная влажность воздуха определяется уравнением 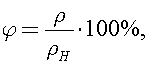где 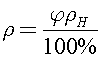-плотность водяных паров в аудитории. Тогда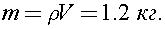
Ответ: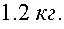

15)В герметически закрытом сосуде объемом V = 5 л находится только кипящая вода массой m₁ = 500 г и ее пары при температуре
t = 100 °С и атмосферном давлении p₀ = 10⁵ Па. Найдите массу m пара. Плотность воды r при 100 °Ссчитать равной 10³ кг/м³. Ответ представьте в граммах и округлите до целого.
Решение:
Найдем объем воды в сосуде: 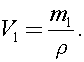Тогда объем пара в сосуде: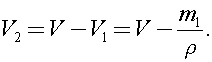
Молярная масса воды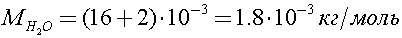
Согласно уравнению Клапейрона - Менделеева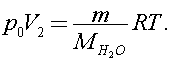
Откуда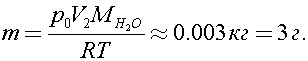
Ответ: 3 г.

16)До какой температуры T₂ необходимо изобарно нагреть m = 700 г азота, находящегося при температуре T₁= 291 К, чтобы работа А расширения газа оказалась равной 4,15×10⁴ Дж? Ответ представьте в единицах СИ и округлите до целого.
Решение:

При изобарном нагревании работа расширения газа равна 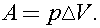Согласно уравнению Клапейрона - Менделеев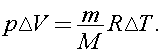а Тогда 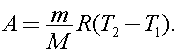Откуда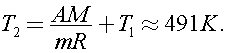

Ответ: