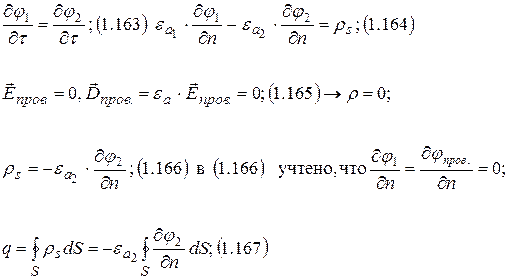Электростатическое поле. Уравнения Пуассона и Лапласа
РАЗДЕЛ №1. ОБЩИЕ ЗАКОНОМЕРНОСТИ ЭЛЕКТРОМАГНИТНЫХ ЯВЛЕНИЙ
ТЕМА №1. ОБЩИЕ ЗАКОНОМЕРНОСТИ ЭЛЕКТРОМАГНИТНЫХ ЯВЛЕНИЙ
Математический аппарат для описания электромагнитного поля (ЭМП).
Градиент
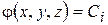 .
.
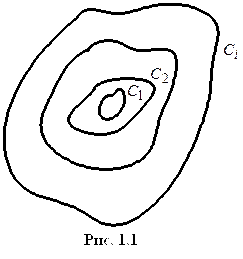
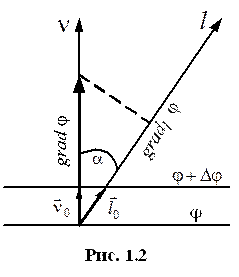
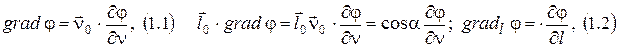
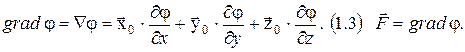

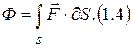
Дивергенция
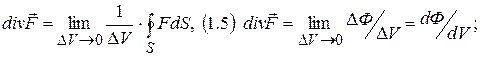

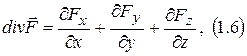
Ротор
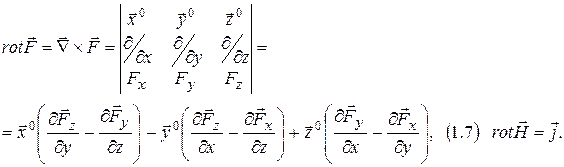
Замечание:
1) 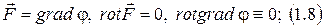
2) 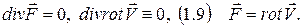
Физические величины характеризующие ЭМП
Источники ЭМП
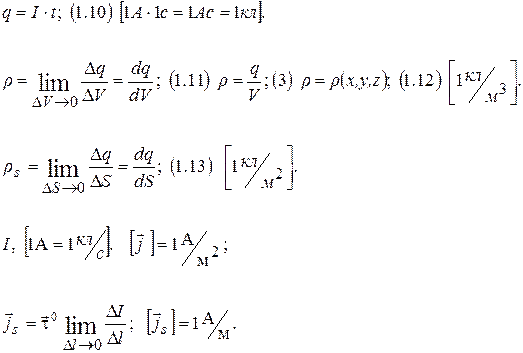
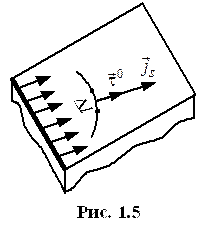
Векторы ЭМП
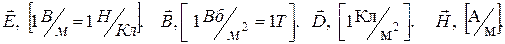
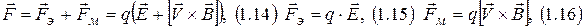
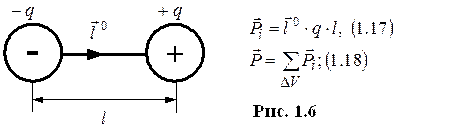
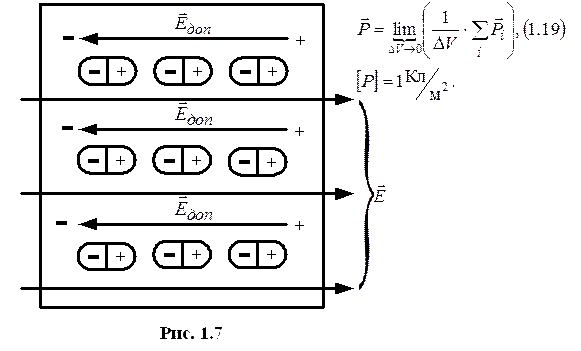
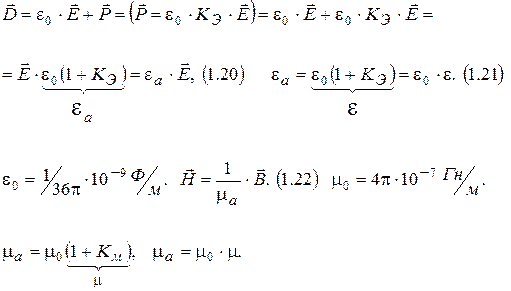
1.3 Законы электродинамики
Законы электродинамики в интегральной форме.
Закон.
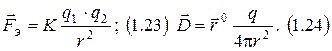
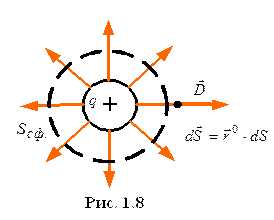
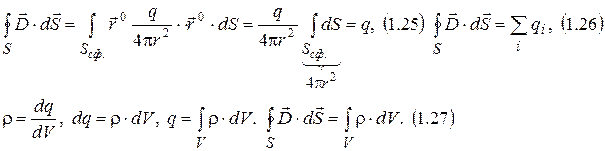
 4 закон.
4 закон.

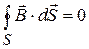 (1.28)
(1.28)
 2 закон.
2 закон.

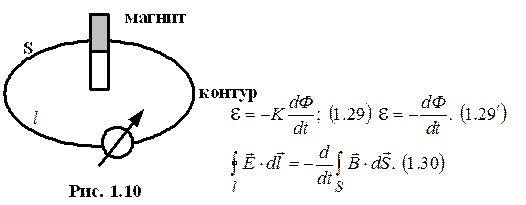
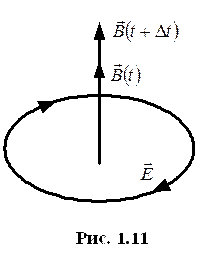
Закон.
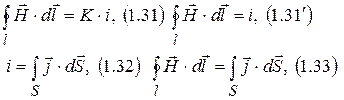
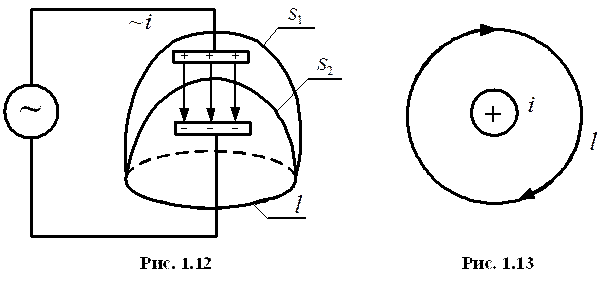
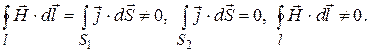

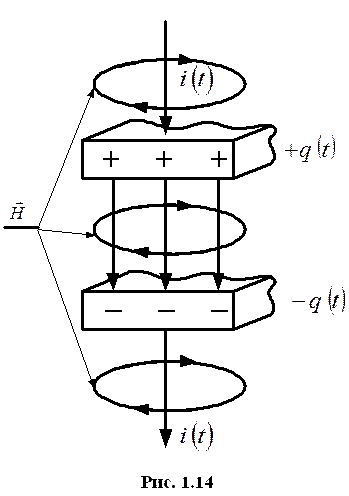
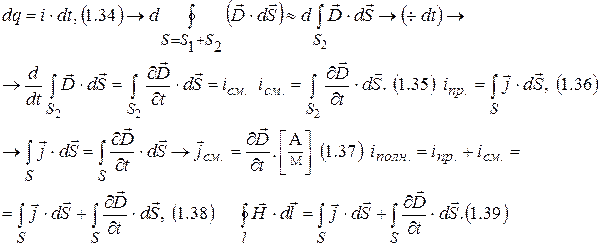
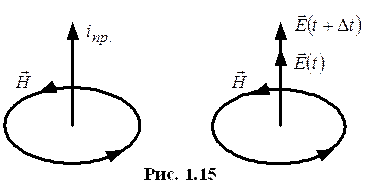
Законы электродинамики в дифференциальной форме.
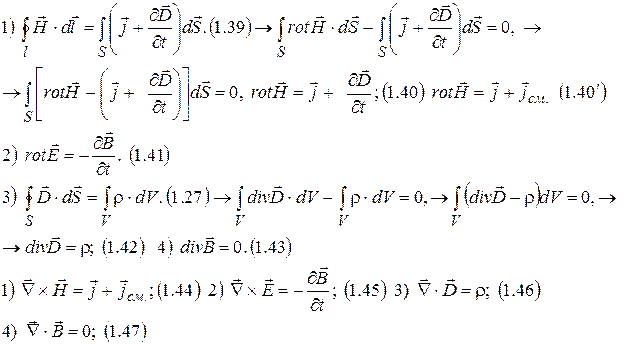
Законы электродинамики в комплексной форме.
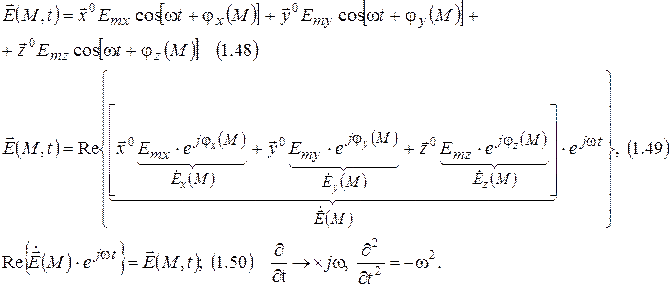
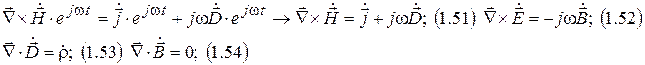
Электромагнитные свойства и классификация сред.
Диэлектрические свойства вещества.
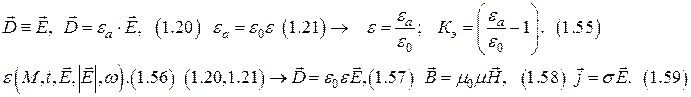
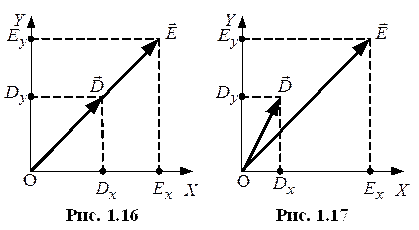
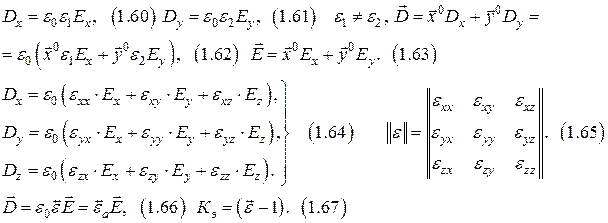
Магнитные свойства вещества.
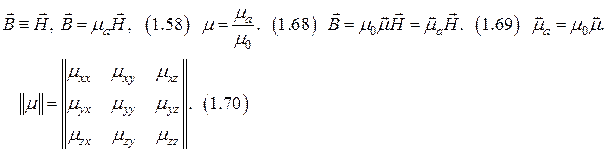
Проводящие среды.
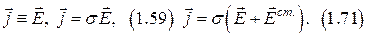
Общие следствия, вытекающие из уравнений Максвелла.
Непрерывность полного тока.
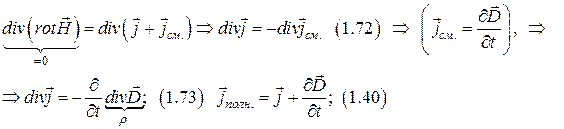
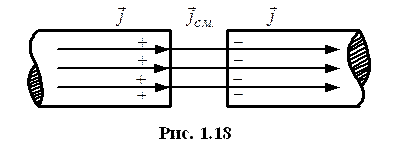
Закон сохранения заряда.
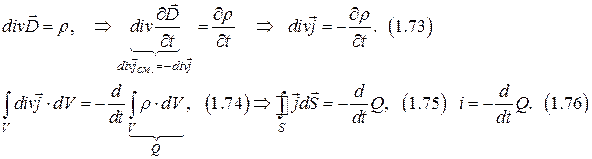
Волновые свойства ЭМП.
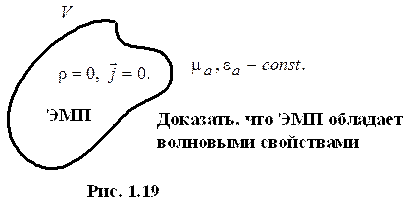
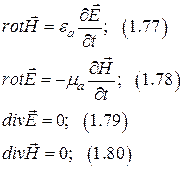 |
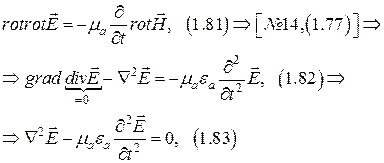 |

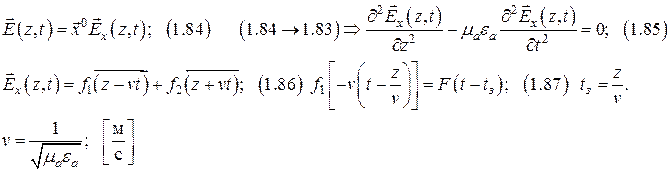
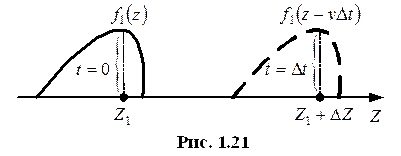
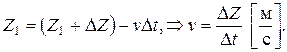
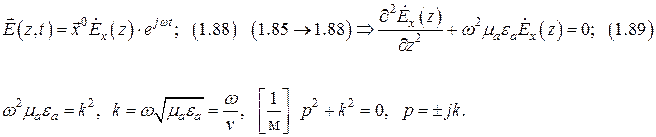
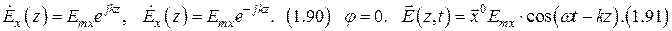
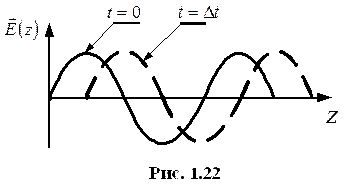
Граничные условия для векторов ЭМП.
Постановка задачи.
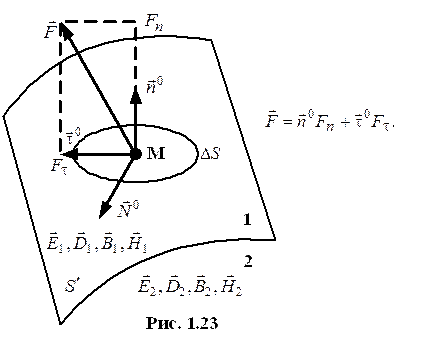
Граничные условия для векторов электрического поля.
а) граничные условия для нормальной составляющей вектора 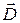 .
.
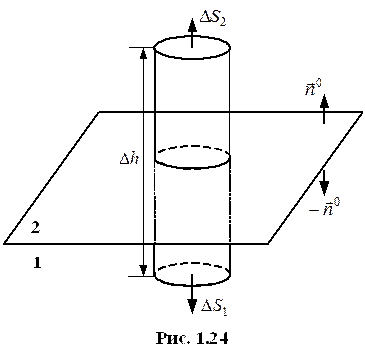
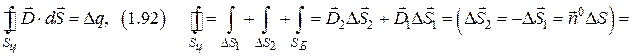
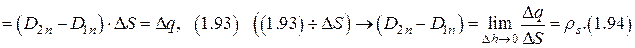
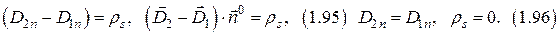
б) граничные условия для тангенциальной составляющей вектора 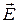
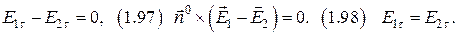
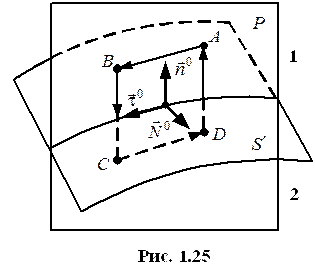 | 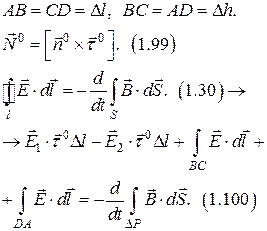 |
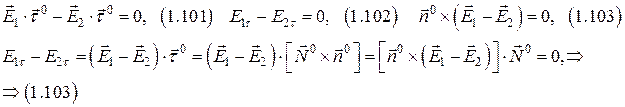
Граничные условия для векторов магнитного поля.
а) граничные условия для нормальной составляющей вектора 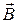 .
.
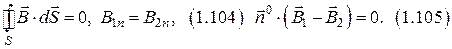
б) граничные условия для тангенциальной составляющей вектора 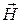
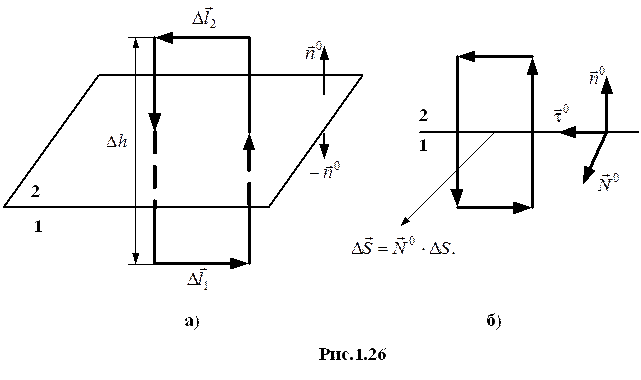
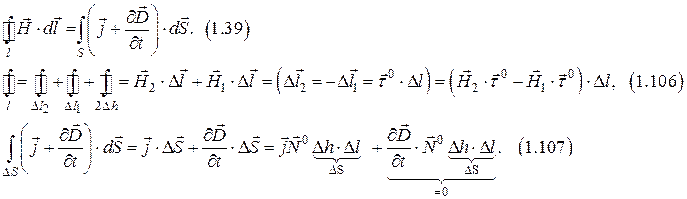
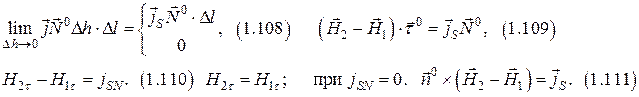
Полная система граничных условий.
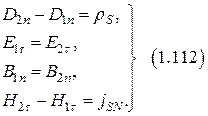  | 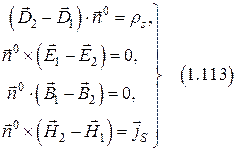 |
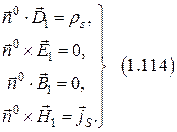 | 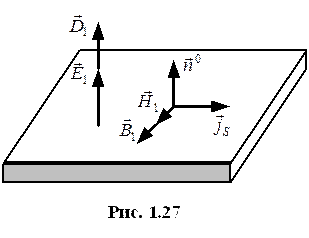 |
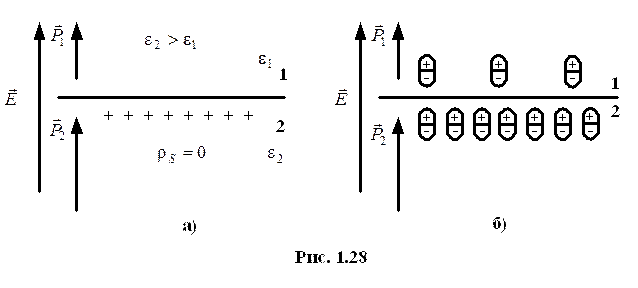
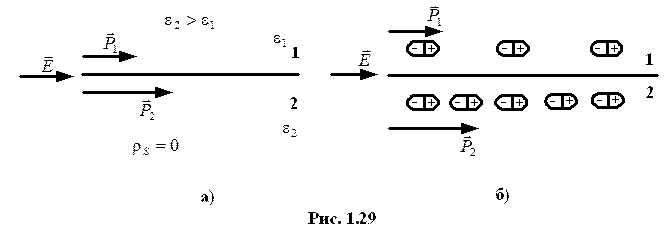
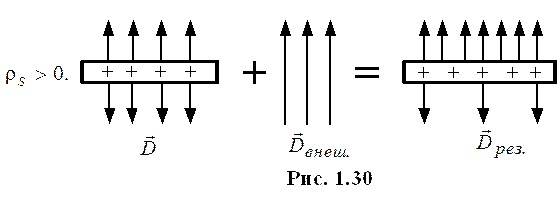

Методы получения волновых уравнений ЭМП.
1.7.1 Метод непосредственного определения векторов 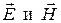 .
.
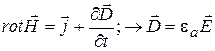 и применим операцию
и применим операцию 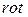 к левой и правой части уравнения
к левой и правой части уравнения 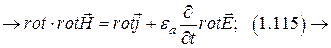 применим п. 14 списка формул и учтем что
применим п. 14 списка формул и учтем что 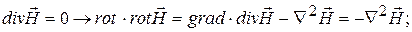
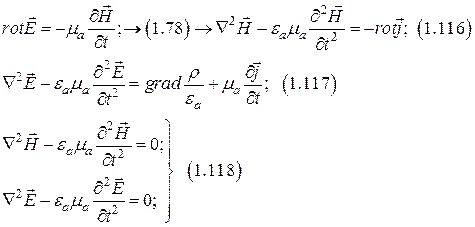
(1.116…1.118) – уравнения Даламбера.
В случае гармонических полей:
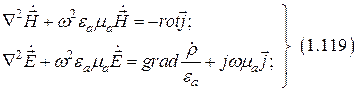 - уравнения Гельмгольца.
- уравнения Гельмгольца.
6 скалярных уравнений второго порядка.
Метод электродинамических потенциалов.
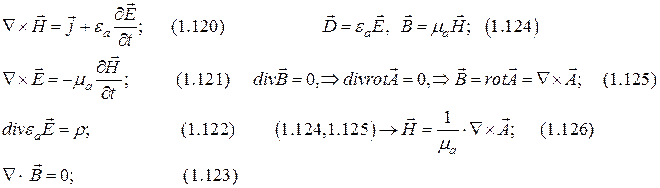
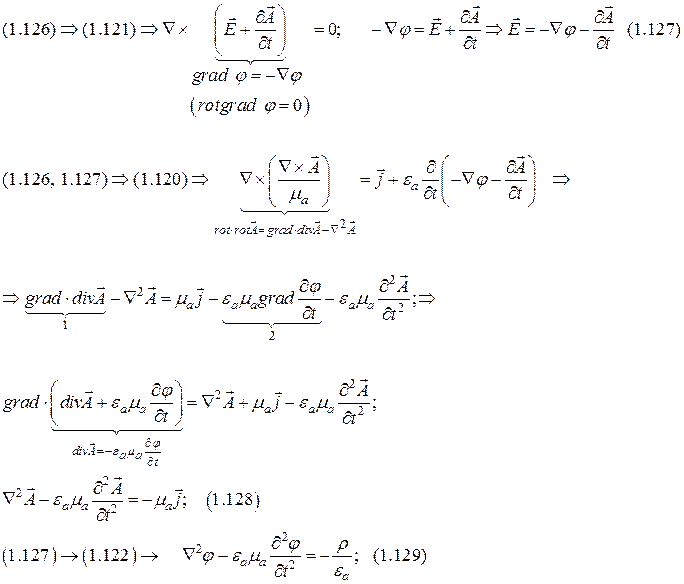
3 - скалярных уравнения соответствующие потенциалу 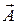 и 1 - скалярное уравнение -
и 1 - скалярное уравнение - 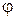 .
.
Понятие о методе вектора Герца.
Метод основан на том, что векторный и скалярный потенциалы, связанные нормировочным соотношением Лоренца могут быть выражены через вектор Герца 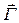 . Потенциалы приобретают вид
. Потенциалы приобретают вид
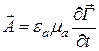 , (1.130)
, (1.130)
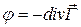 . (1.131)
. (1.131)
(1.130)→ (1.128) Получим уравнения для вектора Герца.
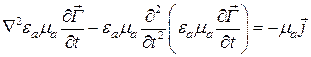
или, изменив порядок дифференцирования по времени и координатам
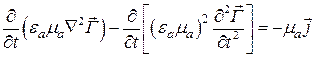 . (1.132)
. (1.132)
Интегрирование (1.132) по времени приводит к трехмерному волновому уравнению
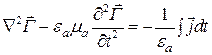 ,
,
решив которое можно найти вектор 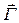 .
.
Определив вектор Герца, вектора поля найдем воспользовавшись соотношениями (1.126) и (1.127) в которые подставим значения потенциалов (1.130), (1.131) получим
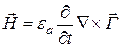 ,
,
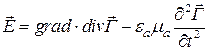 .
.
Энергетические соотношения в ЭМП.
1. 8. 1 Общая формулировка законов сохранения

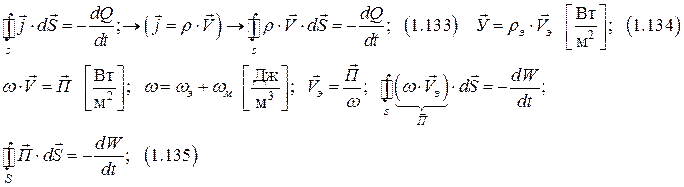
Теорема Умова-Пойтинга
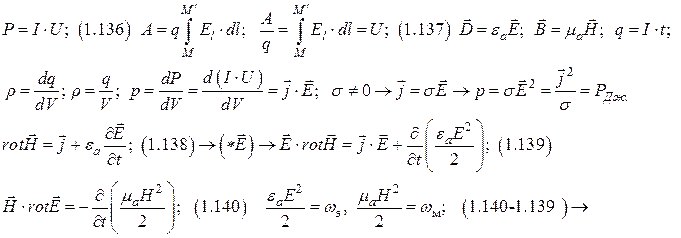
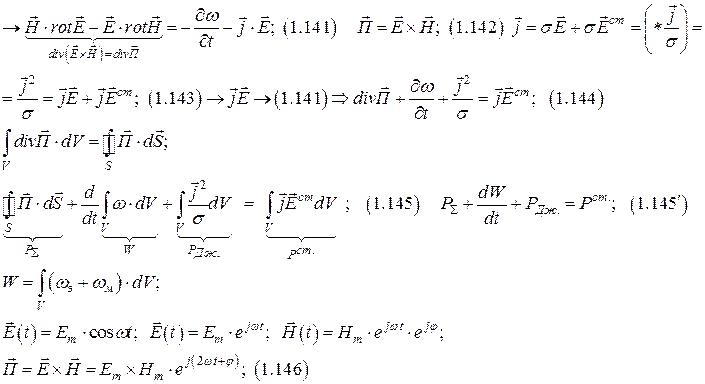
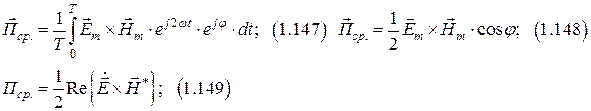
Классификация электромагнитных явлений
Статическое поле Стационарное поле
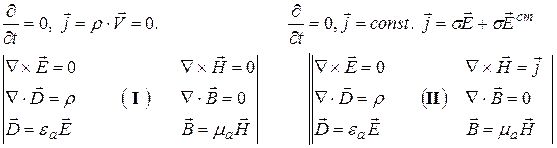
Квазистационарное поле Быстропеременное поле
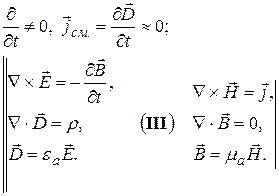
Электростатическое поле. Уравнения Пуассона и Лапласа.
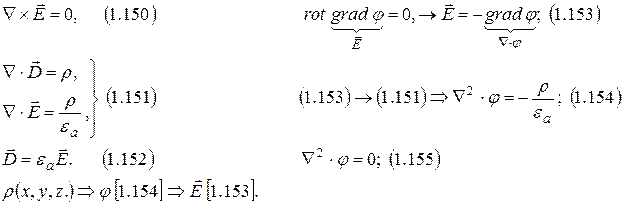
1.8.5. Свойства потенциала φ
1) 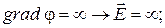
2) 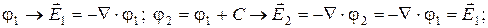
3) 
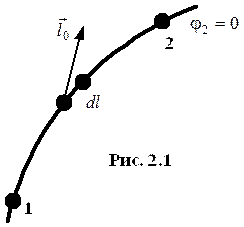 | 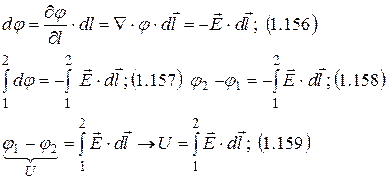 |
4) 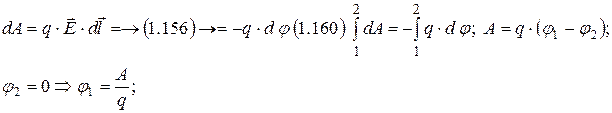
5) φ-функция ограниченная.
6) 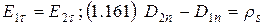 (1.162)
(1.162)