Решить задачу на тему «Дискретная случайная величина»
1. Число телефонных звонков, поступающих в справочное бюро от абонентов между полуднем и часом дня в любой день недели, есть случайная величина X, заданная так:
| xi | ||||||
| pi | 0,3 | 0,2 | P3 | 0,1 | 0,1 | 0,1 |
а) предполагая, что задан закон распределения случайной величины X, найти 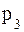 ,
,
б) найти функцию распределения случайной величины X,
в) определить вероятность того, что в справочное бюро поступит больше двух звонков в течение часа (между полуднем и часом дня).
2. Дискретная случайная величина X может принимать только два значения: 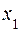 и
и 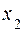 , причем
, причем  . Известны вероятность
. Известны вероятность 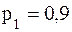 возможного значения
возможного значения 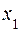 , математическое ожидание M[X] = 2,2, дисперсия D[X] = 0,36. Найти:
, математическое ожидание M[X] = 2,2, дисперсия D[X] = 0,36. Найти:
а) неизвестные 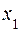 ,
, 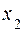 и
и 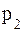 ,
,
б) функцию распределения случайной величины.
3. Число ошибок на страницу, которое делает некоторая машинистка, есть случайная величина X, заданная следующим образом:
| xi | |||||||
| pi | 0,01 | 0,09 | 0,30 | P4 | 0,20 | 0,10 | 0,10 |
а) предполагая, что задан закон распределения случайной величины X, найти p4,
б) найти функцию распределения случайной величины X,
в) определить вероятность того, что ею будет сделано не более 4 ошибок на страницу,
г) определить вероятность того, что машинистка сделает более двух ошибок на страницу.
4. Процент людей, купивших новое средство от головной боли после того, как увидели его рекламу по телевидению, есть случайная величина, заданная так:
| xi | ||||||
| pi | 0,10 | P2 | 0,35 | 0,20 | 0,10 | 0,05 |
а) предполагая, что задан закон распределения случайной величины X, найти 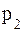 ,
,
б) найти функцию распределения случайной величины X,
в) определить вероятность того, что более 20% людей откликнутся на рекламу.
5. Дискретная случайная величина X может принимать только два значения: 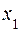 и
и 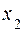 , причем
, причем  . Известны вероятность p1 = 0,8 возможного значения
. Известны вероятность p1 = 0,8 возможного значения 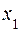 , математическое ожидание M[X] = 3,2, дисперсия D[X] = 0,16. Найти:
, математическое ожидание M[X] = 3,2, дисперсия D[X] = 0,16. Найти:
а) неизвестные 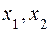 и
и 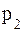 ,
,
б) функцию распределения случайной величины.
6. Число продаваемых машин в автомагазине – случайная величина, заданная так:
| xi | ||||||
| pi | 0,1 | 0,1 | 0,2 | 0,2 | P5 | 0,1 |
а) предполагая, что задан закон распределения случайной величины, найти 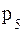 ,
,
б) найти вероятность того, что завтра число проданных автомобилей будет от 2 до 4 (включая 2 и 4),
в) составить функцию распределения числа автомобилей, продаваемых ежедневно.
7. Число иногородних судов, прибывающих ежедневно под погрузку в определенный порт, - случайная величина X, заданная так:
| xi | ||||||
| pi | P1 | 0,2 | 0,4 | 0,1 | 0,1 | 0,1 |
а) предполагая, что задан закон распределения случайной величины, найти 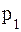 ,
,
б) найти функцию распределения,
в) найти вероятность того, что в заданный день прибудет от 1 до 4 грузовых судов (включая 1 и 4),
г) если в заданный день прибывает больше трех судов, то порт берет на себя ответственность за издержки вследствие необходимости нанимать дополнительных водителей и грузчиков. Чему равна вероятность того, что порт понесет дополнительные расходы в заданный день?
8. Дискретная случайная величина X может принимать только два значения: 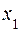 и
и 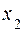 , причем
, причем  . Известны вероятность
. Известны вероятность 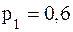 возможного значения
возможного значения 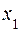 , математическое ожидание M[X] = 3,4, дисперсия D[X] = 0,24. Найти:
, математическое ожидание M[X] = 3,4, дисперсия D[X] = 0,24. Найти:
а) неизвестные 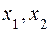 и
и 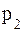 ,
,
б) функцию распределения случайной величины.
9. Число яхт, сходящих со стапелей маленькой верфи, - случайная величина, заданная следующим образом:
| xi | |||||||
| pi | 0,20 | 0,20 | 0,30 | 0,10 | 0,10 | P6 | 0,05 |
а) предполагая, что задан закон распределения случайной величины, найти 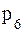 ,
,
б) чему равна вероятность того, что число яхт, построенных в следующем месяце, будет находиться между 4 и 7 (включая 4 и 7)?
в) найти функцию распределения,
г) оценить вероятность того, что число яхт, построенных в течение месяца, будет не более 6.
10. Число дефектов в продукции, производимой автоматом, - случайная величина X, заданная следующим образом:
| xi | |||||
| pi | 0,1 | 0,2 | 0,3 | P4 | 0,1 |
а) предполагая, что задан закон распределения случайной величины, найти p4,
б) найти P(1 < X < 3),
в) построить функцию распределения,
г) определить P(2 ≤ X < 4).
11. Дискретная случайная величина X может принимать только два значения: 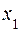 и
и 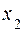 , причем
, причем  . Известны вероятность
. Известны вероятность 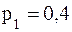 возможного значения
возможного значения 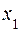 , математическое ожидание M[X] = 3,6, дисперсия D[X] = 0,24. Найти:
, математическое ожидание M[X] = 3,6, дисперсия D[X] = 0,24. Найти:
а) неизвестные 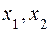 и
и 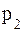 ,
,
б) функцию распределения случайной величины.
12. Доход от некоторого рискованного бизнеса представляет собой случайную величину с заданным рядом распределения:
| xi | -2000 | -1000 | ||||
| pi | 0,1 | 0,1 | 0,2 | 0,2 | 0,3 | 0,1 |
Замечание: -2000, -1000 означают убыток.
а) какой наиболее вероятный денежный доход рискованного бизнеса?
б) чему равен на длительный период средний доход от этого бизнеса?
13. Журнал «Деньги» в одном из номеров поместил информацию о том, что возврат инвестиций на российском рынке в 1990г. ожидался более высоким, чем от аналогичных инвестиций на американском рынке. Консультант по инвестициям, советующий вкладывать средства в российский рынок, полагает, что вероятностное распределение возврата инвестиций (% в году) в один из таких проектов имеет вид:
| xi | |||||||
| pi | 0,05 | 0,15 | 0,30 | 0,20 | 0,15 | 0,10 | P7 |
а) предполагая, что задан закон распределения случайной величины, найти p7,
б) построить функцию распределения,
в) чему равна вероятность того, что возврат инвестиций будет составлять, по крайней мере, 12%.
14. Дискретная случайная величина X может принимать только два значения: 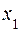 и
и 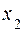 , причем
, причем  . Известны вероятность
. Известны вероятность 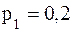 возможного значения
возможного значения 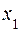 , математическое ожидание M[X] = 3,8, дисперсия D[X] = 0,16. Найти:
, математическое ожидание M[X] = 3,8, дисперсия D[X] = 0,16. Найти:
а) неизвестные 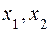 и
и 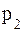 ,
,
б) функцию распределения случайной величины.
15. Распределение случайной величины X – числа бракованных изделий, производимых в течение смены на одном из станков, – задано таблицей:
| xi | ||||
| pi | 0,2 | P2 | 0,3 | 0,1 |
а) найти неизвестную вероятность p2;
б) построить функцию распределения;
в) чему равна вероятность того, что число бракованных изделий будет не больше 2?
16. На полиметаллическом руднике из забоя взято 7 проб. Случайная величина X – результаты химических анализов на содержание металла по пробам.
| xi | |||||||
| pi | 0,1 | 0,3 | 0,1 | P4 | 0,2 | 0,1 | 0,1 |
а) предполагая, что задан закон распределения случайной величины, найти 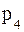 ,
,
б) построить функцию распределения,
в) чему равна вероятность P(3 < X < 6).
17. Испытывается устройство, состоящее из четырех независимо работающих приборов. Случайная величина X – число отказавших при испытании приборов.
| xi | |||||
| pi | 0,3 | 0,2 | 0,1 | P4 | 0,1 |
a) предполагая, что задан закон распределения случайной величины, найти 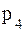 ,
,
б) построить функцию распределения,
в) чему равна вероятность того, что число отказавших приборов не менее 2,
г) чему равна вероятность того, что число отказавших приборов не более 2,
д) чему равна вероятность того, что число отказавших приборов от 1 до 3?
18. Автоматическая линия может выпускать бракованные изделия даже при нормальной настройке. Переналадка линии производится после второго бракованного изделия. Число изделий изготовленных между двумя переналадками линии, есть случайная величина X, заданная таблицей
| xi | ||||||
| pi | 0,05 | P2 | 0,3 | 0,2 | 0,15 | 0,1 |
а) предполагая, что задан закон распределения случайной величины, найти 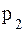 ,
,
б) построить функцию распределения,
в) чему равна вероятность того, что число изготовленных изделий между двумя переналадками больше 300,
г) чему равна вероятность того, что число изготовленных изделий между двумя переналадками меньше 240,
д) чему равна вероятность того, что число изготовленных изделий между двумя переналадками от 220 до 370.
19. Число телефонных звонков, поступающих в справочное бюро от абонентов между полуднем и часом дня в любой день недели, есть случайная величина X, заданная так:
| xi | ||||||
| pi | 0,3 | 0,2 | 0,2 | Р4 | 0,1 | 0,1 |
а) предполагая, что задан закон распределения случайной величины X, найти 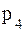 ,
,
б) найти функцию распределения случайной величины X,
в) определить вероятность того, что в справочное бюро поступит больше трех звонков в течение часа между полуднем и часом дня.
20. Процент людей, купивших новое моющее средство после того, как увидели его рекламу по телевидению, есть случайная величина, заданная так:
| xi | ||||||
| pi | 0,10 | 0,25 | 0,35 | P4 | 0,10 | 0,05 |
а) предполагая, что задан закон распределения случайной величины X, найти 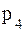 ,
,
б) найти функцию распределения случайной величины X,
в) определить вероятность того, что не менее 25% людей откликнутся на рекламу.
21. Случайная величина X – число отобранных всхожих семян для посева – задана таблицей:
| xi | ||||
| pi | 0,15 | 0,35 | P3 | 0,25 |
а) предполагая, что задан закон распределения случайной величины X, найти 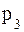 ,
,
б) найти функцию распределения случайной величины X,
в) определить вероятность того, что более 80 семян отобрано для посева.
22. Число прижившихся кустов рассады есть случайная величина X, заданная распределением:
| xi | ||||||
| pi | P1 | 0,3 | 0,1 | 0,2 | 0,1 | 0,1 |
а) найти 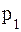 ,
,
б) найти функцию распределения случайной величины X,
в) определить вероятность того, что менее 8 кустов рассады приживется.
23. Случайная величина Х – число родившихся ягнят, имеющих хорошие наследственные признаки, в некотором хозяйстве - задана следующей таблицей:
а) предполагая, что задан закон распределения случайной величины X, найти 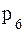 ,
,
б) найти функцию распределения случайной величины X,
в) определить вероятность того, что число родившихся ягнят, имеющих хорошие наследственные признаки, заключено в интервале от 90 до 108.
24. Число продаваемых машин в автомагазине – случайная величина, заданная так:
| xi | ||||||
| pi | 0,05 | 0,1 | P3 | 0,15 | 0,4 | 0,1 |
а) предполагая, что задан закон распределения случайной величины, найти p3,
б) найти вероятность того, что завтра число проданных автомобилей будет от 2 до 4 (включая 2 и 4),
в) составить функцию распределения числа автомобилей, продаваемых ежедневно.
25. Число иногородних судов, прибывающих ежедневно под погрузку в определенный порт, - случайная величина X, заданная так:
| xi | ||||||
| pi | 0,1 | 0,15 | 0,35 | P4 | 0,1 | 0,1 |
а) предполагая, что задан закон распределения случайной величины, найти 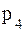 ,
,
б) найти функцию распределения,
в) найти вероятность того, что в заданный день прибудет от 1 до 4 грузовых судов (включая 1 и 4),
г) если в заданный день прибывает больше трех судов, то порт берет на себя ответственность за издержки вследствие необходимости нанимать дополнительных водителей и грузчиков. Чему равна вероятность того, что порт понесет дополнительные расходы в заданный день?
26. Число покупателей, совершивших покупку в магазине, есть случайная величина X, заданная законом распределения:
| xi | ||||||||
| pi | 0,05 | 0,10 | 0,15 | 0,05 | 0,25 | 0,05 | P7 | 0,15 |
а) найти 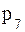 ,
,
б) составить интегральную функцию распределения,
в) найти вероятность того, что число покупателей, совершивших покупку в магазине, больше 40.
27. Число дефектов в продукции, производимой автоматом, - случайная величина X, заданная следующим образом:
| xi | |||||
| pi | 0,1 | P2 | 0,3 | 0,2 | 0,1 |
а) предполагая, что задан закон распределения случайной величины, найти 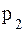 ,
,
б) найти P(2 < X < 4),
в) построить функцию распределения,
г) определить P(1 < X < 4).
28. Распределение случайной величины X – числа контрольных работ с оценкой «отлично», извлеченных из пачки, - задано таблицей:
| xi | |||||||
| pi | 0,05 | P2 | 0,15 | 0,30 | 0,20 | 0,15 | 0,10 |
а) найти 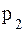 ,
,
б) построить функцию распределения,
в) определить вероятность того, что число контрольных работ с оценкой «отлично» будет не более 2.
29. Доход от некоторого рискованного бизнеса представляет собой случайную величину с заданным рядом распределения:
| xi | -2000 | -1000 | ||||
| pi | 0,1 | 0,2 | 0,2 | 0,1 | 0,3 | 0,1 |
Замечание: -2000, -1000 означают убыток.
а) какой наиболее вероятный денежный доход рискованного бизнеса?
б) чему равен на длительный период средний доход от этого бизнеса?
30. Число автобусов, выезжающих ежедневно на линию по определенному маршруту, есть случайная величина X, заданная следующей таблицей:
| xi | |||||
| pi | 0,1 | 0,2 | P3 | 0,3 | 0,1 |
а) считая, что задан закон распределения, найти p3,
б) составить функцию распределения,
в) найти вероятность того, что число автобусов вышедших на линию не менее 2.
31. Число яхт, сходящих со стапелей маленькой верфи, - случайная величина, заданная следующим образом:
| xi | |||||||
| pi | Р1 | 0,20 | 0,30 | 0,10 | 0,10 | 0,15 | 0,05 |
а) предполагая, что задан закон распределения случайной величины, найти 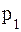 ,
,
б) чему равна вероятность того, что число яхт, построенных в следующем месяце, будет находиться между 2 и 5 (включая 2 и 5)?
в) найти функцию распределения,
г) найти вероятность того, что число яхт, построенных в течение месяца, будет не менее 6.
32. Число проданных кондуктором трамвая проездных билетов – случайная величина X, заданная распределением:
| xi | |||||||
| pi | 0,1 | 0,15 | 0,25 | 0,25 | P5 | 0,05 | 0,05 |
а) найти 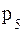 ,
,
б) найти функцию распределения,
в) считая, что стоимость одного билета равна 6 руб. Найти среднюю выручку кондуктора.
33. Процент людей, купивших новое обезболивающее средство после того, как увидели его рекламу по телевидению, есть случайная величина, заданная так:
| xi | ||||||
| pi | 0,10 | 0,25 | 0,35 | 0,20 | 0,10 | Р6 |
а) предполагая, что задан закон распределения случайной величины X, найти 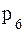 ,
,
б) найти функцию распределения случайной величины X,
в) определить вероятность того, что не менее 30% людей откликнутся на рекламу.
34. Вероятностный прогноз для величины X – процентного изменения стоимости акций по отношению к их текущему курсу в течение 6 месяцев – дан в виде закона распределения:
| xi | ||||||
| pi | 0,1 | 0,1 | 0,2 | 0,3 | 0,2 | Р6 |
а) найти 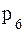 ,
,
б) построить функцию распределения,
в) найти вероятность того, что курс акций будет более 19%.
35. Пусть ежедневные расходы на обслуживание и рекламу автомобилей в некотором автосалоне составляют в среднем 100 тыс. руб., а число продаж X автомашин в течение дня подчиняется следующему закону распределения:
| xi | ||||||||||
| pi | 0,25 | 0,2 | 0,1 | 0,1 | 0,1 | 0,1 | 0,05 | 0,05 | 0,025 | 0,025 |
а) Найти математическое ожидание ежедневной прибыли при цене за машину 150 тыс. руб. (Указание: ежедневная прибыль рассчитывается по формуле: П = (150Х – 100) тыс. руб.)
б) построить функцию распределения.
Задание 10
Дана плотность распределения f(x) случайной величины X (см. табл.1).
Найти:
а) параметр g;
б) математическое ожидание случайной величины X;
в) дисперсию случайной величины X;
г) функцию распределения F(x) случайной величины X;
д) вероятность выполнения неравенства x1 < X < x2.
Построить графики функций f(x) и F(x).
Таблица 1.1
Индивидуальные данные для задания 10
| n | f(x) | параметры | x1 | x2 |
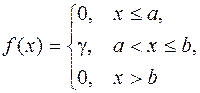 | a = -1, b = 3 | |||
| a = 0, b = 5 | -1 | |||
| a = 1, b = 3 | ||||
| a = -2, b = 4 | -1 | |||
| a = -3, b = 3 | ||||
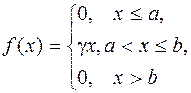 | a = 0, b = 2 | |||
| a = 1, b = 4 | ||||
| a = 3, b = 7 | ||||
| a = 4, b = 5 | ||||
| a = 0, b = 3 | ||||
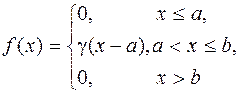 | a = 1, b = 3 | |||
| a = -1, b = 1 | ||||
| a = 2, b = 6 | ||||
| a = 6, b = 8 | ||||
 31 31 | a = -5, b = -1 | -4 | ||
| Продолжение табл.1.1 | ||||
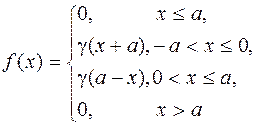 | a = 1 | |||
| a = 2 | -1 | |||
| a = 3 | -2 | |||
| a = 4 | -5 | |||
| a = 5 | ||||
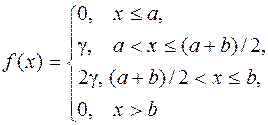 | a = 1, b = 3 | |||
| a = 3, b = 7 | ||||
| a = 2, b = 5 | ||||
| a = -2, b = 4 | ||||
| a = -1, b = 5 | -1 | |||
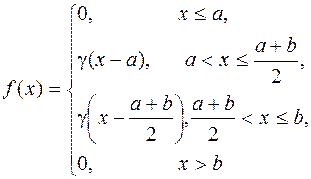 | a = 0, b = 1 | -1 | 0,25 | |
| a = -1, b = 1 | 0,5 | |||
| a = 2, b = 4 | 3,5 | |||
| a = 1, b = 4 | ||||
| a = 10, b = 12 | ||||
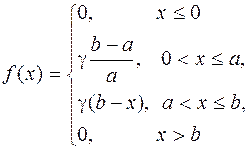 | a = 1, b = 2 | 1,5 | ||
| a = 1, b = 3 | 0,5 | |||
| a = 2, b = 3 | ||||
| a = 0,5, b = 1 | 0,5 | |||
| a = 1, b = 1,5 | 0,5 |
Задание 11
Дана плотность распределения 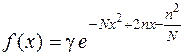 случайной величины X. Найти:
случайной величины X. Найти:
а) математическое ожидание случайное величины X,
б) дисперсию случайной величины X,
в) параметр g,
г) функцию распределения F(x) случайной величины X,
д) вероятность P(-N < X – M[X] < D[X]),
е) такое d, что 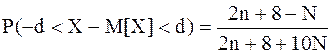 .
.
Построить графики функций f(x) и F(x).
Задание 12
