Автор тестов: к.ф.-м.н., доц. Романков В.В

1. В автобусе едут 8 женщин и 3 мужчины. На остановке из автобуса вышли 3 женщины и 1 мужчина, а зашли в автобус 2 женщины и 2 мужчины и один мальчик. Вероятность того, что на следующей остановке первой сойдет женщина равна:

1. В урне находятся 3 белых шара и 4 черных. Из урны один за другим вынимаются 2 шара. Вероятность того, оба вынутых шара белые равна:

1. В семье растут 2 мальчика и 3 девочки. На экскурсию в столицу в порядке поощрения должны быть отправлены два ребенка. Вероятность того, что будут отправлены две девочки равна

1. В урне находятся 2 белых шара и 6 черных. Из урны наугад вынимается один шар, затем опускается назад в урну и шары в урне перемешиваются. После этого снова вынимается один шар. Вероятность того, что оба вынимаемых шара черные равна

1. Имеются два одинаковых на вид ящика. В первом ящике находятся 1 белый шар и 2 черных, во втором ящике 2 белых шара и пять черных. Из наудачу выбранного ящика взят 1 шар. Вероятность того, что этот шар белый равна

1. Два стрелка производят по одному выстрелу по цели. Вероятность попадания в цель первого стрелка 0,6, вторым стрелком – 0,4. Вероятность того, что в цель попадут оба стрелка равна

1. Два стрелка производят по одному выстрелу по цели. Вероятность попадания в цель первого стрелка 0,7, вторым стрелком – 0,6. Вероятность того, что цель поражена равна

1. Производится серия выстрелов по цели. Вероятность попадания в цель при одном выстреле равна ¾. Вероятность двух попаданий при трех выстрелах равна

1. Производится 4 выстрела по цели. Вероятность попадания в цель при одном выстреле равна 1/2. Вероятность трех попаданий равна

1. Производится 3 выстрела по цели. Вероятность попадания в цель при одном выстреле равна 2/3. Вероятность не более одного промаха равна

1. Вероятность попадания в цель при одном выстреле равна 3/5. Вероятность двух промахов при трех выстрелах равна
2. Пусть Х – дискретная случайная величина, заданная законом распределения вероятностей

Х	-2
Р	0,3	?	0,5

Математическое ожидание этой случайной величины равно

13. Пусть Х – дискретная случайная величина, заданная законом распределения вероятностей

Х	-1
Р	?	0,3	0,1

Математическое ожидание этой случайной величины равно

14. Пусть Х – дискретная случайная величина, заданная законом распределения вероятностей

Х
Р	0,2	0,3	?

Математическое ожидание этой случайной величины равно

15. Пусть Х – дискретная случайная величина, заданная законом распределения вероятностей

Х	-1	-2
Р	0,1	0,2	?

Математическое ожидание этой случайной величины равно

16. Непрерывная случайная величина Х задана плотностью распределения вероятностей .

Математическое ожидание этой нормально распределенной случайной величины равно

17. Непрерывная случайная величина Х задана плотностью распределения вероятностей .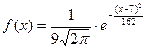

Математическое ожидание этой нормально распределенной случайной величины равно

18. Непрерывная случайная величина Х задана плотностью распределения вероятностей .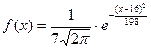

Среднее квадратическое отклонение этой нормально распределенной случайной величины равно

19. График плотности распределения вероятностей непрерывной случайной величины Х, распределенной равномерно в интервале (-2;3) имеет вид

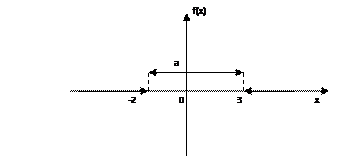
Значение а равно

20. График плотности распределения вероятностей непрерывной случайной величины Х, распределенной равномерно в интервале (-1;5) имеет вид

Значение а равно

21. Пусть Х – дискретная случайная величина, заданная законом распределения вероятностей

Х	-2
Р	0,3	?	0,4

Математическое ожидание этой случайной величины равно

22. Пусть Х – дискретная случайная величина, заданная законом распределения вероятностей

Х
Р	0,2	0,1	?

Математическое ожидание этой случайной величины равно

23. Пусть Х – дискретная случайная величина, заданная законом распределения вероятностей

Х	-3
Р	?	0,6	0,3

Математическое ожидание этой случайной величины равно

24. Непрерывная случайная величина Х задана плотностью распределения вероятностей .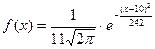

Математическое ожидание этой нормально распределенной случайной величины равно