Проверка оптимальности найденного решения критерием оптимальности стратегии
Стратегия P* и Q* называется оптимальной, а число V – цена игры если справедливо неравенство M (P,Q*) ≤ V ≤ M (P*,Q), где P и Q – произвольные стратегии.
Критерий оптимальности стратегий.
Для того что бы P* и Q* были оптимальными стратегиями соответствующих игроков, а число V было ценой игры необходимо и достаточно что б выполнялось неравенство M (Pi,Q*) ≤ V ≤ M (P*,Qi).
Теорема Джона фон Неймана (основная).
Любая матричная игра имеет решение т.е. существуют оптимальные стратегии и цена игры.
Седловой точкой называется Аij, которая является наименьшим элементом в своей строке и наибольшим элементом в столбце.
Если матрица имеет седловую точку, то игра имеет решение в чистых стратегиях. Если Седловых точек нет, то одна из оптимальных стратегий будет смешана.
Если одна из компонент стратегий равна 1, то остальные нулю, то стратегия называется чистой в противном смешанной.
Доминирующая строка – все элементы этой строки не превосходят соответствующих элементов другой строки.
Доминирующий столбец – все элементы не меньше соответствующих элементов какого-либо другого столбца.
Делаем проверку
P1 = (1, 0, 0)
P2 = (0, 1, 0)
P3 = (0, 0, 1)
Q1 = (1, 0, 0, 0)
Q2 = (0, 1, 0, 0)
Q3 = (0, 0, 1, 0)
Q4 = (0, 0, 0, 1)
M (P*,Q1) = 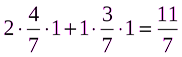
M (P1,Q*) = 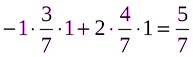
M (P1,Q*) ≤ V ≤ M (P*,Q1)
5/7 ≤ 5/7 ≤ 11/7
M (P*,Q2) = 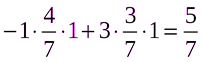
M (P2,Q*) = 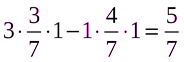
M (P2,Q*) ≤ V ≤ M (P*,Q2)
5/7 ≤ 5/7 ≤ 5/7
M (P*,Q3) = 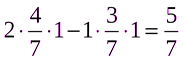
M (P3,Q*) = 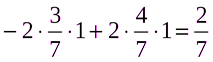
M (P3,Q*) ≤ V ≤ M (P*,Q3)
2/7 ≤ 5/7 ≤ 5/7
ЗАКЛЮЧЕНИЕ
В результате проведенной работы проанализирована литература по данной теме и решение задачи. В моем курсовом проекте нужно решить игру в смешанных стратегиях и сделать проверку. Исходные данные: платежная матрица, найти оптимальную стратегию и цену игры. Данную задачу можно решить при помощи математических методов. Что бы решить ее нужно построить математическую модель и решить эту модель симплексы методом (максимум). Я построил математическую модель. Так же решал симплекс метод при помощи компьютера (MS Excel Поиск решения) и на бумаге. Сделав анализ, что меньше времени уходит на решение, если решать на компьютере, чем на бумаге Все данные сошлись, а так же сошлась и проверка при помощи Поиск решения..
Цена игры равна 1, а оптимальный план равен P* и Q*
Поставленная задача была мною решена.
Библиографический список
- А.В. Могилев, Н.И. Пак, Е.К. Хеннер, «Информатика»: Учеб. пособие для студ. пед. вузов,Под ред. Е.К. Хеннер –М.: изд. Центр «Академии »,2000
- Н.Ш. Кример, Б.А. Путков , М.Н. Фридман, «Исследовательские операции в экономики»: Учеб. пособие для вузов, Под ред проф. Н.Ш. Кример-М.: Юнити, 2006
- И.К Волков, Е.А Загоруйко, «Исследовательские операции»: Учеб. для вызов 2-е издание, Под ред В.С. Зарубина , А.П. Кришенко –М.: Из-во МГТУ ими Н.Э.Баумана 2002
- Элементы теории игр. Учеб. пособие для студ. -1 изд., стер-М.: Высш. шк., 1999
- Под ред. В.И. Ермакова, «Сборник задач по высшей математике для экономистов»: Учеб. пособие, Москва: ИНФА-М, 2002
- Конспект по дисциплине «Математические методы»
- Е.С. Вентцель, «Элементы теории игр», Государственное издательство физико-математической литературы, Москва, 1961
