Математическое описание САУ.
Костромской государственный технологический университет
Кафедра автоматики и микропроцессорной техники
Задание для студентов заочного факультета спец. 2102
по ТЕОРИИ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ч.1
КОНТРОЛЬНАЯ №1
1. тема «Типовые динамические звенья»
Составить таблицу дифференциальных уравнений и передаточных функций основных типовых звеньев (безинерционного усилительного, интегрирующего, дифференцирующего, апериодического 1 порядка, инерционного звена 2 порядка, звена запаздывания).
Провести исследование заданного типового динамического звена (дифференциальное уравнение звена, передаточная функция, выражения и график переходной характеристики, выражения и графики частотных характеристик, включая логарифмические).
| Вариант | Тип звена | К | Т1, с | r | Т2, с | t, с |
| Апериодическое 1 порядка | 0.1 | |||||
| Интегрирующее | ||||||
| Звено 2 порядка | 0,5 | 0,4 | 0,2 | |||
| Дифференцирующее | 0,25 | |||||
| Апериодическое 2 порядка | 0,1 | |||||
| Звено 2 порядка | 0,4 | 0,6 | ||||
| Апериодическое 1 порядка | 0,5 | 0,5 | ||||
| Звено 2 порядка | 0,5 | 1,2 | ||||
| Звено запаздывания с усилением | 0,8 | |||||
| Звено 2 порядка | 0,2 | |||||
| Интегрирующее | ||||||
| Дифференцирующее | 0,5 | |||||
| Апериодическое 1 порядка | 0,1 | |||||
| Звено 2 порядка | 0,1 |
- Тема «Структурные схемы САУ и их преобразование»
Выписать правила основных структурных преобразований (звено, узел, сумматор, последовательное, параллельное соединения, соединение с обратной связью, перенос узла и сумматора через звено) – сжато, не более страницы.
Исследовать характеристики звена , охваченного жесткой отрицательной обратной связью (вывести передаточную функцию, привести к типовому звену, сделать выводы).
a) Kи
W1(p)= --------;
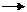
P _ W1(p)
б) Ko
W1(p) = ----------- Kос
T p + 1
| Вариант | |||||||||||||
| Ки | 0,1 | 0,2 | 0,4 | 0,5 | 0,1 | 0,2 | 0,5 | 0,4 | 0,1 | 0,2 | 0,4 | 0,5 | 0,2 |
| Ко | |||||||||||||
| Т | 0,2 | 0,4 | 0,5 | 0,2 | 0,4 | 0,5 | 0,2 | 0,4 | 0,5 | 0,2 | 0,4 | 0,5 | 0,1 |
| Кос |
Заданную структурную схему преобразовать и получить передаточную функцию разомкнутой системы, передаточные функции замкнутой системы по управлению Wзу(p), по ошибке Wзе(p), по возмущению Wзf(p).
| Вариант | |||||||||||||
| схема |
Схема 1
f
Uз e Кп К1 - K2 У
- - Т1×р+1 р
Ки
р
К3
К4
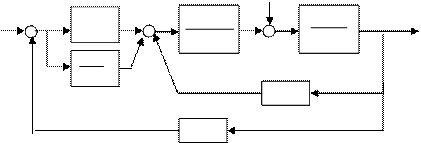
Схема 2
f
Uз e Кп К1 - K2 У
- Т1×р+1 - р
Ки
р
К3
К4
Схема 3
f
Uз e Кп К1 - K2 У
- - Т1×р+1 Т2×р+1
Ки
р
К3
К4
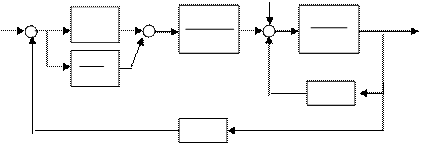
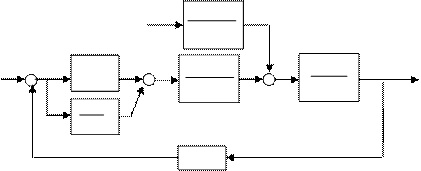Схема 4
К3
f То×р+1
Uз e Кп К1 - K2 У
- Т1×р+1 Т2×р+1
Ки
р
К4
Схема 5
К3
f То×р+1
Uз e Кп К1 - K2 У
- Т1×р+1 р
Ки
р
К4
КОНТРОЛЬНАЯ № 2
1. тема «Установившиеся режимы в САУ».
Считая коэффициенты Ки, Кп неизвестными, исследовать установившийся режим заданной системы. Схему системы взять из контрольной работы №1 п.2.3.
- определить величину статической ошибки в системе еуст;
- определить значение Ки, обеспечивающее скоростную ошибку еуст < 0,01 (1% ) для линейно нарастающего Uзд = a t.
Остальные параметры системы приведены в таблице
| Вариант | |||||||||||||
| а | 0,1 | 0,2 | 0,4 | 0,5 | 0,1 | 0,2 | 0,5 | 0,4 | 0,1 | 0,2 | 0,4 | 0,5 | 0,2 |
| К1 | |||||||||||||
| К2 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,1 | 0,2 | 0,3 |
| К3 | 0,3 | 0,2 | 0,1 | 0,3 | 0,2 | 0,1 | 0,3 | 0,2 | 0,1 | 0,3 | 0,2 | 0,1 | 0,3 |
| К4 | |||||||||||||
| То | |||||||||||||
| Т1 | 0,8 | 0,7 | 0,6 | 0,5 | 0,8 | 0,7 | 0,6 | 0,4 | 0,8 | 0,7 | 0,6 | 0,5 | 0,8 |
| Т2 | 0,1 | 0,2 | 0,3 | 0,4 | 0,1 | 0,2 | 0,3 | 0,4 | 0,1 | 0,2 | 0,3 | 0,4 | 0,1 |
| схема |
- Тема «Устойчивость САУ».
Используя критерий устойчивости Гурвица, найти критическое значение Кп.
Построить годограф Михайлова для Кп = Кп крит, 0,5 Кп крит, 2 Кп крит.
Аналогично предыдущему проверить устойчивость системы по критерию Найквиста.
Для случая устойчивой системы построить логарифмическую амплитудно-частотную (ЛАЧХ) и фазочастотную (ЛФЧХ) характеристики разомкнутой системы, определить запас устойчивости по амплитуде и по фазе.
Примечание: при использовании критерия Найквиста не забывайте в передаточной функции разомкнутой системы учитывать и цепь обратной связи (петлевое усиление).
- Тема «Переходные процессы в САУ».
Для значения Кп, соответствующего устойчивой системе, построить переходный процесс в системе по управлению и по возмущению.
Определить временные показатели качества процесса регулирования:
-установившуюся ошибку (остаточное отклонение) D;
-максимальное динамическое отклонение DУmax;
-перерегулирование s %;
-время регулирования tр;
-степень колебательности m;
-степень затухания Y.
Содержание дисциплины.
Вводная часть курса.
Основные задачи ТАУ, термины и определения. История развития науки. Принципы построения. Классификации САУ. Технические примеры.
Математическое описание САУ.
Понятие о звене САУ и статической характеристике. Типовые входные воздействия, переходная и импульсная характеристики. Описание объектов управления в структурно-операторной форме. Понятие о передаточной функции, свойства преобразования Лапласа. частотные характеристики. Типовые динамические звенья и их свойства. Описание объектов управления в пространстве состояний. Структурная схема САУ. Методы структурных преобразований. Передаточные функции при различных соединениях звеньев.
Статические режимы.
Понятие о точности управления в установившемся режиме. Статические системы и методы их анализа и синтеза в установившемся режиме. Астатические системы, их достоинства и недостатки. Практические факторы, влияющие на точность в установившемся режиме.
Устойчивость САУ.
Понятие устойчивости: математическое и физическое. Связь устойчивости с корнями характеристического уравнения. Алгебраические критерии устойчивости Рауса, Гурвица. Принцип аргумента, частотные критерии устойчивости Михайлова, Найквиста, их сравнительная оценка. Понятие областей устойчивости, D-разбиение. Влияние запаздывания на устойчивость САУ.