Одна из задач функциональной надежности

Расчет на этапе проектирования

Звездочки палки

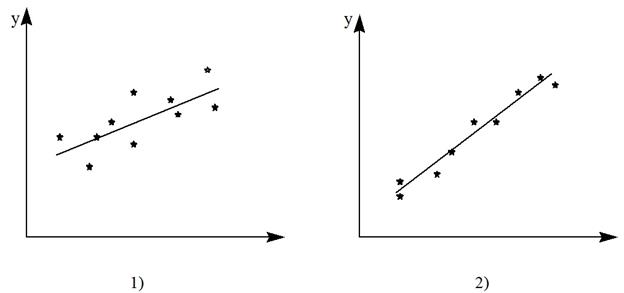
		2-Сильная зависимость , byx – велико, разброс мал
		1-Слабая зависимость, byx – мало, разброс велик

Объем выборки

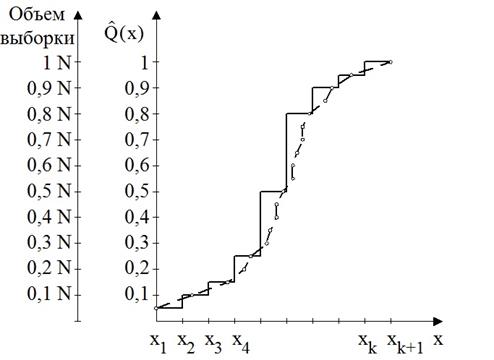
		Интенсивность событий

Значение случайной величины, которое делит пополам площадь под кривой плотности распределения называется

		Медианой

Показатели надежности объектов, с каким временем восстановления, вычисляются только в календарном времени?

с конечным временем восстановления

Математическое ожидание наработки на отказ восстанавливаемого объекта определяется как отношение общей наработки к _

математическому ожиданию числа его отказов в течение этой наработки

Оценка параметра потока событий (отказов или восстановлений) при условии, что все отказавшие объекты заменяются исправными или восстанавливаются, может быть найдена по формуле:

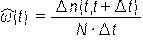
При стационарном потоке отказов вероятность безотказной работы на интервале Δt

		F(Δt) = exp(−ω⋅Δt)

Большая часть задач функциональной надежности требует следующего подхода

		Параметрического

Суть метода получения моментов системы состоит в

		Расчете моментов объекта по характеристикам элементов и заданной функции объекта

Число поездов на фидерной зоне подчиняется:

		Биноминальному закону

Решая систему уравнений Колмогорова для графа состояний в модели отказа с марковской аппроксимацией параметра, мы получим:

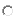		вероятность этих состояний
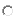		интенсивности восстановления i – того состояния
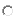		среднюю наработку на отказ
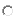		интенсивности перехода в i – тое состояние

Параллельное соединение (по надежности) применяется для

		Повышения надежности системы

Все последовательно соединенные (по надежности) элементы, от которых зависит передача электроэнергии к узлу, объединенных в один эквивалентный элемент это

		Схема одного состояния

Матрицу путей можно составить и с учетом надежности узлов, это приводит к тому, что увеличится

		Число столбцов

Чему равна наработка до отказа системы с параллельным (по надежности) соединением

Наработке до отказа элемента у которого она оказалась наибольшей

Марковская аппроксимация параметра постепенного и внезапного отказа выглядит следующим образом:

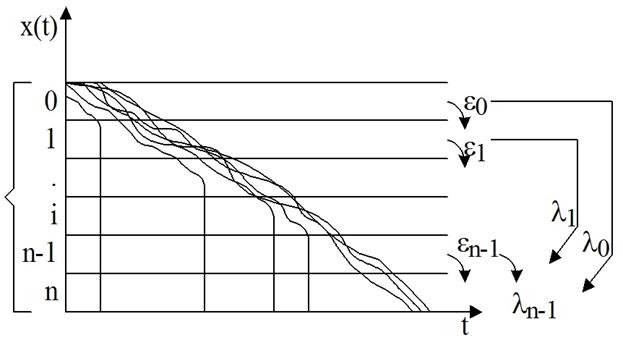
Истина

Объект, для которого в рассматриваемой ситуации проведение восстановления работоспособного состояния не предусмотрено в нормативно технической и (или) конструкторской (проектной) документацией