Многоцелевая оптимизация. Методы экспертных оценок

Во всех без исключения сферах своей деятельности человек сталкивается с проблемой многоцелевой оптимизации [5]. При этом в подавляющем большинстве случаев он принимает решения не на основании каких-то строгих математических построений, а, используя предшествующий опыт (чаще всего - неосознанно) и интуицию (которая сама по себе есть некоторый синтез этого опыта, умноженный на талант ЛПР).

Однако в последние десятилетия многоцелевая опти­мизация все более и более становится предметом исследования математическими методами, которые развиваются и используются в двух основных направлениях: для анализа неопределенности и анализа полезности. Суть анализа полезности состоит в следующем. Обычно полностью обеспечить выполнение разных целей невозможно. Всегда в какой-то мере приходится жертвовать полным выполнением одних ради выполнения других целей, т. е. довольствоваться некоторым компромиссным решением. Причиной этого является противоречивость целей. Характерным примером являются две цели - экономичность и надежность. Как правило, повышение надежности осуществляется за счет ухудшения экономиичности и наоборот.

Таким образом, поиск компромиссных решений является центральной задачей многоцелевой оптимизации. При этом различные цели имеют в разных ситуациях различную ценность. Следовательно, компромиссное решение должно осуществляться на основе предпочтений одних целей над другими. Но как это сделать? Ведь во всех главных случаях предпочтения не имеют численной меры, т. е. отсутствуют условия, опираясь на которые можно было бы математически строго соизмерить разные цели в каком-либо едином масштабе. В этих условиях математические методы должны быть направлены на такой предварительный отбор и такое описание оставшихся альтернатив, чтобы ЛПР получил по возможности ясное представление, по крайней мере, о качественной стороне достоинств и недостатков этих альтернатив. На этой основе ЛПР может уже принять более или менее мотивированное решение о выборе оптимальной альтернативы (с точки зрения ЛПР).

Ниже кратко рассмотрены методы, предназначенные для анализа предпочтений.

Выбор решений в условиях многокритериальности и неопределенности обычно выполняется ЛПР с учетом мнения экспертной комиссии. Оно формируется с помощью определенного метода получения экспертных оценок отдельных экспертов и итоговой экспертной оценки комиссии. Ниже кратко рассмотрены несколько таких методов.

Метод балльных оценок. Эксперты ставят свои оценки каждому критерию (весовые коэффициенты) в еди­ной шкале относительных оценок. Затем исследователь, отвечающий за обработку экспертных оценок, выводит по определенному правилу итоговую относительную оценку каждого критерия. Известно несколько таких правил:

1. Все эксперты считаются равнокомпетентными. В этом случае итоговая оценка является среднеарифметической.

2. Предварительно каждый эксперт анонимно (как правило, при соблюдении тайны) ставит относительные балльные оценки компетентности экспертов по одному из двух вариантов (принятому в данной процедуре): оценки ставятся или только себе, или всем экспертам, кроме себя. Во втором варианте выводятся средние оценки. Оценки критериев, представленные экспертами, умножаются на нормированные весовые коэффициенты компетентности экспертов и после этого подсчитываются итоговые оценки.

Второй вариант оценки экспертов достаточно деликатен в психологическом плане и пригоден не для каждого состава экспертов.

К рассмотренным правилам 1 и 2 добавляют еще одно: перед определением итоговых оценок критериев отбрасываются верхние и нижние оценки каждого критерия.

Метод балльных оценок обычно находит применение в случаях сопоставления простых критериев, когда их можно не представлять в виде совокупности частных критериев более низкого ранга. Если же критерии сложные (например, критерий надежности), то их предварительно разделяют на более простые частные критерии, для которых определяют оценки. Затем осуществляется формальный переход к оценкам исходных критериев.

Для выполнения предпочтений часто используют так называемые бинарные отношения, когда выполняется попарное сравнение всех критериев.

Метод Борда — Лапласа. Для более детального представления о методе балльных оценок рассмотрим одну из его разновидностей, предназначенную для определения предпочтительных альтернатив А или В (метод можно использовать и для нескольких альтернатив).

В дополнение к альтернативам А и В группе экспертов r = 1, 2, ..., R предъявляются вспомогательные альтернативы Ci, i = 1, 2, ..., n и предлагается для A и B сов­местно с Ci назначить числа xmr, m = 1, 2, ..., n + 2 на отрезке [0,1]. Условно принимают, что меньшие числа означают большие предпочтения. Затем определяются средние баллы предпочтительностей альтернатив A и B:

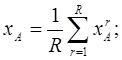
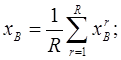
Их разность указывает на предпочтительность одной из этих альтернатив и дает представление об интенсив­ности этого предпочтения. Считается, что увеличение числа экспертов и вспомогательных альтернатив повышает правдоподобность решения.

Наиболее сомнительное решение будет в предельном случае при двух экспертах и противоречивости их мнений.

Таблица 2.4.Матрица экспертных оценок альтернатив

Первый эксперт	Альтернативы	А	С1	С3	С4	С2	С5	В
xm1	0	0,1	0,3	0,5	0,6	0,8	1,0
Второй эксперт	Альтернативы	В	С1	С4	А	С2	С3	С5
xm2	0	0,2	0,4	0,6	0,8	0,9	1,0

В табл.2.4 представлен такой пример при n = 5, причем предпочтительности убывают слева направо.

Из табл.2.4 можно понять, что эксперты приняли разные интенсивности предпочтений: первый эксперт считает более интенсивным предпочтение А над В (xB1 – xA1 = 1,0), второй эксперт - предпочтение B над A (xA2 – xB2 = 0,6).

Решение принимается на основе принципа минимакса (см. 2.3), который в данном случае требует, чтобы при ошибочном решении ущерб был минимальным. Если считать, что он пропорционален разности баллов для А и В отвергнутой рекомендации, то решение должно быть принято в пользу более интенсивного предпочтения, т. е. следует считать А предпочтительнее В.

Слабым местом в этом приеме является использование пропорциональности между ущербом и разностью баллов, поскольку последняя является субъективной и её правильность не гарантирована.

В дальнейшем была предложена вероятностная модель метода Борда - Лапласа. В ней используются те же данные экспертизы и поэтому качественный вывод о предпочтительности одной альтернативы над другой сохраняется.

Кроме того, иногда считают, что упорядоченный набор чисел в порядке возрастания, выставленный каждым экспертом всем n + 2 альтернативам, является одной из реализации (n + 2) - мерной случайной величины x, равномерно распределенной в области своих значений. Такая модель позволяет получить численные значения доверительных вероятностей предпочтений одних альтернатив над другими, что несколько улучшает представление о количественных характеристиках предпочтений. Однако применение этой модели при малом числе альтернатив и, особенно при малом числе экспертов сомнительно из-за использования весьма малой выборки.

Таким образом, при любой модели объективность решения зависит от числа сопоставляемых оценок и квалификации экспертов.

Метод дерева целей. Если решаемая проблема (не обязательно сводящаяся к оценке критериев) настолько сложна, что эксперты не в состоянии дать ей достаточно определенную оценку, то такую проблему разделяют на последовательность более простых задач или вопросов (строят дерево целей), находящихся в компетенции экспертов. К подобным проблемам относятся, в част-ности, некоторые вопросы прогнозирования и отыскания оптимальных аспектов дальнейшей деятельности общества или его отдельных подсистем. Вообще же речь идет обычно о сложных многокритериальных проблемах, которые плохо прогнозируются с помощью формальных математических процедур. Однако все эти проблемы должны обладать одним важным свойством - они должны допускать их расчленение на такие более простые цели, каждая из которых зависит только от одной цели более высокого ранга, т. е. цели образуют дерево, не имеющее контуров (рис.2.6)

Экспертные оценки выставляют для простейших целей, причем не обязательно в виде балльных оценок. Они могут быть в виде, например, так называемых «интуитивных вероятностей», когда каждому простому событию эксперт ставит в соответствие некоторую вероятность его существования. Оценки про-стых событий распространяются на более сложные, составные сообщения и т. д. вплоть до оценок всей проблемы в целом.

Метод решающих матриц. Существуют проблемы, где формирование дерева целей невозможно из-за наличия пересекающихся связей, которые отражают взаимные зависимости мероприятий (или целей). Такие задачи возни-кают, например, при распределении ресурсов на выполнение сложных мероприятий, предпочтительность которых не может быть установлена непосредственно, без разло­жения этих мероприятий на более простые и установление зависимостей как внутри каждой ступени, так и между разными ступенями иерархии целей. В этом случае в соответствии со сложным графом целей (рис.2.7) строят матрицы, элементы которых отражают представления экспертов о долях влияния одних мероприятий на выполнение других. Затем мероприятия соответствующим образом группируют относительные важности этих групп. В результате все первоначально сформулированные мероприятия или цели ранжируются по важности, что затем учитывает ЛПР при выборе решения.

Методы дерева целей и решающих матриц содержат одну общую процедуру - разделение сложных целей на более простые, которые в состоянии оценить эксперты. Из этого следует, что качество разделения сложных целей на простые решающим образом влияет на результаты экспертизы. Поэтому естественно иметь на этот счет какие-то общие рекомендации. Однако пока они не разработаны и задача разделения целей остается эвристической, а качество ее решения зависит от квалификации и таланта исследователей, которые ее решают.

Методы организации взаимодействия экспертов. Во всех рассмотренных методах может быть по-разному организован способ взаимодействия экспертов. Они могут, например, до выставления оценок свободно обмениваться мнениями (схема круглого стола), или этот обмен может быть как-то регламентирован, или даже вообще отсутствовать. В конечном счёте это решает исследователь по поручению ЛПР или непосредственно ЛПР.