Основные теоремы дифференциального исчисления

Теорема Ферма: пусть функция 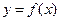определена в замкнутом промежутке [a,b]. Внутренняя точка с этого промежутка принимает наибольшее (наименьшее) значение

- в этой точке существует конечная производная 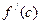. Тогда .

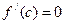Геометрический смысл этой теоремы заключается в следующем: При выполнении условий теоремы в указанной точке 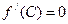т.е. касательная к кривой в этой точке параллельна оси OX. если y=f(x) определена [a,b] (.)c=max(min)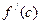

Тогда .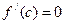

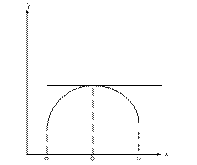
Теорема Ферма может быть неприменима, если в точке C конечной производной нет

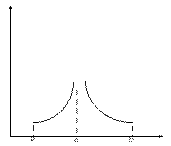
Теорема Ролля.

пусть функция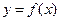

1. определена и непрерывна в замкнутом промежутке [a,b]

2. существует конечная производная 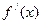хотя бы в отдельном промежутке (a,b)/

3. На концах промежутка функция принимает равные значения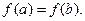

Тогда между a и b найдется такая точка c , что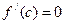

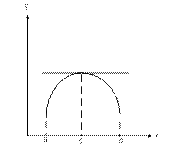
если y=f(x) Определена в [a,b] не прерывна 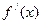в (a,b) тогда f(a)=f(b).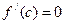

геометрический смысл в том, что при выполнении условий теоремы найдется такая точка C , что в указанной точке 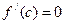, т.е. в указанной точке касательная перралельна оси OX.

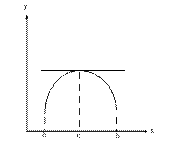
Теорема Лагранжа.

пусть функция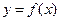

- определена и не прерывна в замкнутом промежутке [a,b].

- существует конечная производная 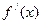хотя бы в определенном промежутке .

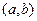тогда между a и b найдется такая точка c, что 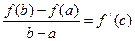полученная формула называется формулой Лагранжа.

Геометрический смысл теоремы Лагранжа следующий..

Касательная в точке c параллельна [a,b].

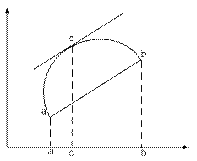
Угловой коэффициент Хорды равен угловому коэффициенту касательной.

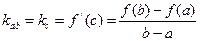
Хорда- отрезок соединяющий две точки окружности

Теорема Коши.

Пусть функции 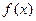и

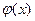
1.определена в замкнутом промежутке [a,b]

2.имеет конечные производные 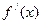и 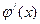хотя бы в прoмежутке (a,b)

3. 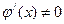в промежутке (a,b) тогда между a и b найдется такая точка c, что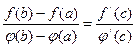

Правило Лапиталя

предел отношения двух бесконечно малых или больших функций равен пределу отношения их производных ( конечному или бесконечному) если такой преднл существует в указанном смысле .

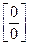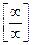Т.е. если имеется неопределенность вида или , то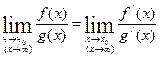

Неопределенность это выражение вида: /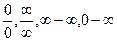

Пример: найти 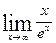имеем неопределенность вида .

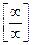Применяя правило Лапиталя получим:

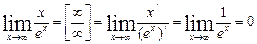
Пример: Найти 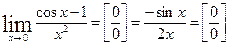, опять неопределима тогда берем вторую производную .

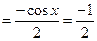пример:

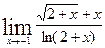в данном случае имеем не определенность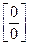

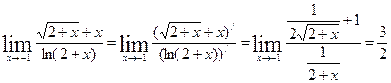
Пример:

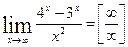применяем правило Лапиталя: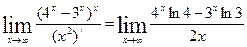

неопределенность вида 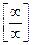остается

применяем правило Лапиталя еще раз получим

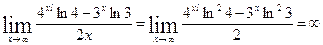
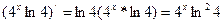
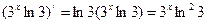
Правило Лапиталя можно применять так же и для раскрытия неопределенностей вида 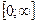Для этого произведение f(x)*g(x) следует записать в виде 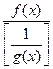или 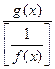получить неопределенность вида : 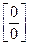или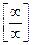

пример: .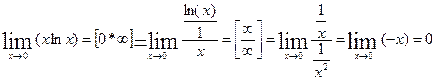

1.

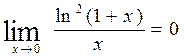
2.

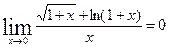
3.

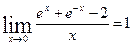
4.

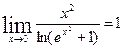
5.

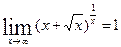
6.

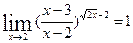
7.

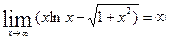
1.

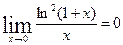
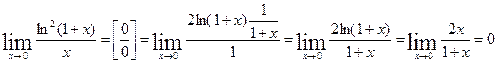
Эквивалентные бесконечные величины при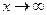

.

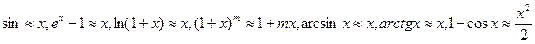2. 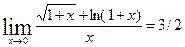имеем неопределенность ,

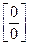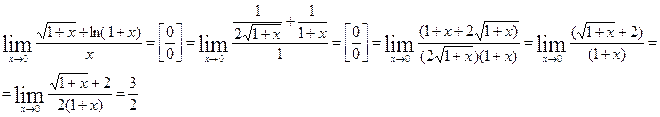
3. 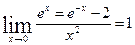имеем неопределенность .

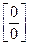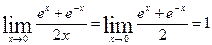
4. 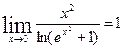имеем неопределенность .

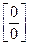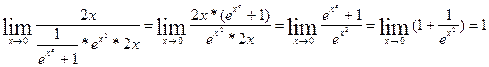
5. 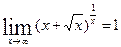неопределенность вида 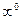имеем сложно показательную функцию дифференцировать такую функцию можно при помощи логарифмического дифференцирования т.е. дифференцирование после предельного логарифмирования т.е.

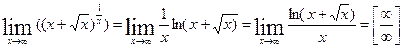
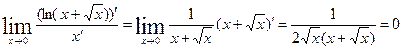
Используем соотношение на основе свойств логарифмов и непрерывности показательной функции.

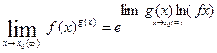
согласно этой формуле

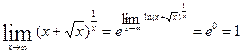
7. 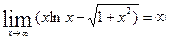имеем неопределенность .

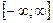Преобразуем предел:

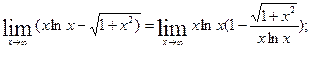найдем отдельно предел по правилу Лапиталя: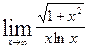

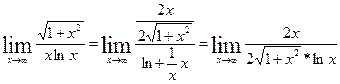
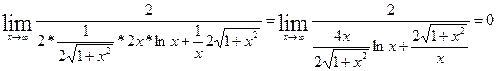
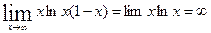
пример1.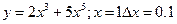

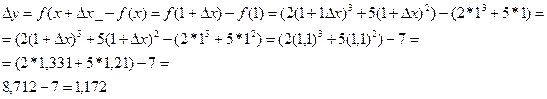
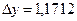
2.

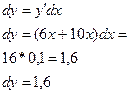
пример: найти дифференциал функции 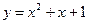точке x=2

1. выделяя линейеую относительно 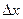часть приращения функции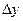

2. по формуле .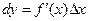

Решение:

1.прирощение функции

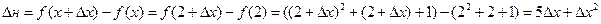
Выделяя линейную относительно 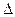x часть прирощения функции получаем что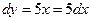

2. Дифференциал функции

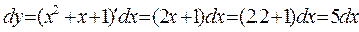
II. Задание и указания обучающимся по подготовке к практическому занятию

При подготовке к практическому необходимо изучить основную и дополнительную литературу.