Дифракция света на щели в параллельных лучах
Для того, чтобы определить результат дифракции в произвольной точке пространства, следует рассчитать интерференцию вторичных волн, попавших в эту точку от волновой поверхности. Рассмотрим простейший случай, когда фронт волновой поверхности имеет форму плоскости. Допустим, что такая плоская волна падает на щель определённой ширины АВ(см.рис.).
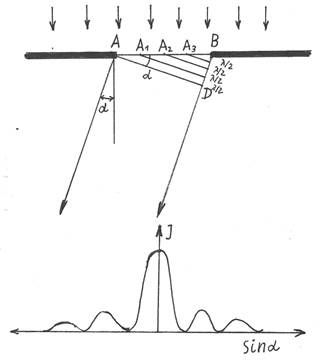
Волновую поверхность при этом разобьём на отдельные участки и назовём их зонами Френеля. Эти зоны расположены так, чтобы математические операции были возможно проще.
Выберем произвольное направление и выясним, каков будет результат интерференции вторичных волн в данном направлении. Проведём перпендикуляр из точки А до линии выбранного направления, где будет точка D. BD – разность хода вторичных волн от точек Аи В. Разобьём это расстояние на отрезки, каждый из которых равен половине длины волны. Таким образом, разделим ширину щели АВ на равные зоны Френеля: АА1 = А1А2 =А2А3 = А3В.Любой вторичной волне, идущей от какой-либо точки одной зоны Френеля, можно найти в соседних зонах Френеля соответствующие вторичные волны такие, что разность хода между ними будет равна половине длины волны. Например, вторичная волна, идущая от точки А2в выбранном направлении имеет сдвиг фаз, равный половине длины волны, по отношению к вторичной волне, идущей от точки А1. Следовательно, эти две волны при распространении просто погасят друг друга.
Число зон, укладывающееся в щели, зависит от длины волны и от угла выбранного нами направления a .Если щель АВразбить на нечётное количество зон Френеля, а разность хода на нечётное количество отрезков, равных половине длины волны, то в выбранном направлении будет наблюдаться максимум:
BDsin a = (2k+1)l/2 (k = 1,2,3…)
Направление, перпендикулярное щели, т.е. a = 0также отвечает максимуму, так как все вторичные волны в данном направлении пойдут в одной фазе и поэтому в данном направлении также будет интерференционный максимум.
Если щель АВразбить на чётное число зон Френеля,то в выбранном нами направлении все волны от попарно расположенных зон Френеля взаимно погасят друг друга и в данном направлении будет наблюдаться минимум:
BDsin a = (2k)l/2 = kl (k = 1,2,3…)
Если на достаточно большом расстоянии от щели поставить экран, то на нём будет видно чередование светлых и тёмных полос. Картина будет симметрична относительно центрального, наиболее яркого максимума. Чем дальше максимум расположен от центрального максимума, тем яркость его будет меньше. Если щель освещать белым светом, то на экране картина будет представлять систему из радужных полос, причём, в каждой радужной полосе фиолетовый конец радужной полоски будет направлен в сторону центрального максимума, так как у фиолетового цвета длина волны будет наименьшей. Однако, центральный максимум будет всё-таки белым, так как в этом месте максимум будет для лучей со всеми длинами волн.
Дифракция на множестве щелей. Дифракционная
Решётка.
Мы рассмотрели случай дифракции света на одной щели. А теперь представим себе систему из множества щелей. Такой системой является дифракционная решётка.
Она бывает двух видов: прозрачнаяи отражательная.
Прозрачная решётка представляет собой прозрачную пластину из стекла или прозрачной плёнки, на которую нанесены множество непрозрачных линий. На практике, в качестве непрозрачных линий на пластину наносят обыкновенные царапины специальным тонким алмазным резцом. Каждая царапина выполняет ту же роль, что и непрозрачная линия.
В отражательной решётке систему царапин наносят на поверхность металлической пластины, отполированной до зеркального блеска. Получается тоже дифракционная решётка, только она действует на отражение.
Важнейшим параметром решётки является её период - d: то есть сумма ширины непрозрачной линии и расстояния между линиями. Часто её характеризуют количеством линий на 1 мм ширины. Самые простые дифракционные решётки используются в школьном демонстрационном эксперименте и они имеют 100 линий на 1 мм ширины и на них написано число 1/100. Лучшие решётки имеют на 1 мм около 2000 штрихов. Такие решётки изготовляются на специальных машинах, которые наносят на подготовленную поверхность штрихи специальным алмазным резцом. Главное требование при этом, чтобы расстояние между всеми штрихами было абсолютно одинаковым. Для этого такая машина работает в специальном помещении, в котором поддерживается строго постоянная температура и перед нанесением штрихов эта машина должна несколько часов подряд работать вхолостую, чтобы окончательно стабилизировались все её параметры
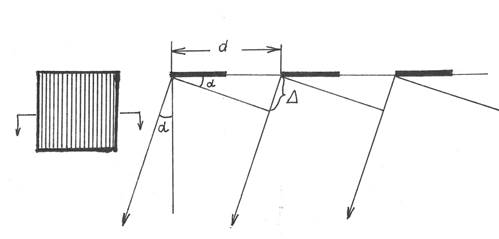
Рассмотрим решётку в поперечном разрезе. Как видно из данного рисунка, в выбранном нами направлении на каждом периоде будет наблюдаться разность хода лучей:
D = d sin a
Для того, чтобы в данном направлении наблюдался максимум, нужно, чтобы на разности хода укладывалось целое число длин волн:
D = d sin a = kl (k = 1,2.3…)
Данная формула называется условием максимума дифракционной решётки.
В результате, при прохождении через дифракционную решётку монохроматического света, на экране будет наблюдаться картина, аналогичная той, которая наблюдалась при дифракции от одной щели. Однако, картина от решётки будет более яркой, так как в построении этой картины принимают участие не одна щель, а множество.
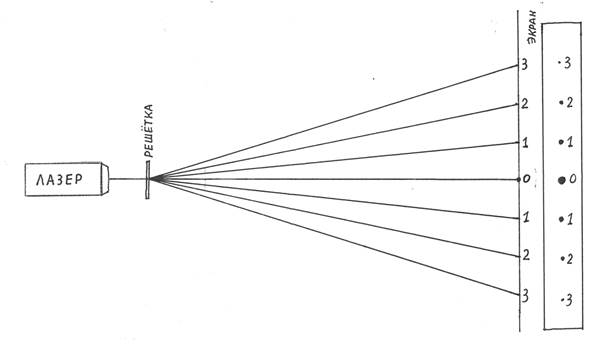
Наглядный опыт можно поставить с помощью лазера. Если луч лазера пустить на экран, то он высветит на экране только одну точку. Если на пути луча лазера поставить дифракционную решётку, то на экране будет наблюдаться картина, состоящая не из одной, а из нескольких точек. Все они будут лежать на одной прямой. Посередине будет самая яркая точка – главный центральный максимум. По обе стороны будут располагаться симметрично максимумы: две ближайшие точки – максимумы первого порядка, на рисунке обозначены цифрой 1. Они образованы тем, что разность хода лучей в этом направлении равна одной длине волны; следующие два максимума – это максимумы второго порядка, на рисунке они обозначены цифрой 2. Они образованы тем, что разность хода лучей в этом направлении равна двум длинам волны и т.д.
Если взять решётку с меньшим периодом, то дифракционная картина будет более растянута, так как для достижения той же самой разности хода лучей при уменьшенном периоде, нужно лучу отклониться на больший угол. Но здесь следует отметить, что период решётки должен всегда быть больше длины световой волны, иначе даже угла выбранного направления 90о будет недостаточно для получения разности хода в одну световую волну. И наоборот: если взять решётку с большим периодом, то картина максимумов будет более сжата. Если же взять решётку с очень большим периодом, то все максимумы всех порядков будут располагаться настолько близко к главному максимуму, что практически сольются с ним и дифракция наблюдаться не будет.
А если решётку освещать светом с меньшей длиной волны, например, освещать вместо красного цвета синим, то дифракционная картина с синими максимумами будет более сжата, так как для достижения определённой разности хода лучей с меньшей длиной волны потребуется отклонение на меньший угол.
Таким образом, дифракционную решётку можно использовать для точного измерения длины волны света.
Если же решётку осветить белым светом, то максимумы будут выглядеть как радужные полоски и называться они будут дифракционными спектрами 1-го, 2-го и последующего порядков. При этом, все спектры будут расположены так, что их фиолетовые концы будут обращены к белому центральному максимуму. Если такую решётку приложить к глазу и посмотреть через неё на удалённый источник белого света, например, на электрическую лампу накаливания, то можно увидеть по обе стороны от лампы радужные полосы – дифракционные спектры различных порядков.
Таким образом, разложить белый свет в спектр можно не только дисперсионной призмой, но и дифракционной решёткой. Но решётка, в отличие от призмы даёт спектр строго линейный, т.е. угол отклонения луча находится в строгой пропорциональности с длиной его волны, что очень важно для научных исследований. Единственный недостаток этого метода, что дифракционный спектр значительно уступает дисперсионному по яркости.
Если понаблюдать за окружающей нас обстановкой, то можно в некоторых местах встретить проявление дифракции света. Например, современный компакт-диск при освещении его прямыми лучами от Солнца или от электролампы выглядит радужно окрашенным, хотя он изготовлен на белой основе. Откуда же берётся цвет? На компакт-диске нанесена спиральная бороздка, в которой записана информация. И витки этой бороздки выполняют роль штрихов в отражательной дифракционной решётке. Ещё один интересный факт можно наблюдать, если смотреть на далёкий источник света через тонкую капроновую материю. Вокруг источника света располагаются спектры, причём, они располагаются в вершинах квадратиков как по горизонтали, так и по вертикали. Это объясняется тем, что материя представляет как бы две дифракционные решётки, сложенные вместе так, что их штрихи перпендикулярны друг другу, так что капроновая материя представляет собой двухмерную дифракционную решётку. В некоторых явлениях природы также можно наблюдать явление дифракции света. Например, в зимний морозный день иногда вокруг Солнца наблюдаются концентрические круги – гало. Это объясняется тем, что в воздухе присутствуют мелкие кристаллики льда, причём, расстояние между ними приблизительно выдерживается одинаковым и они действуют как штрихи дифракционной решётки. Самый внутренний круг соответствует максимуму 1-го порядка, следующий за ним круг большего диаметра – максимуму 2-го порядка и т.д. Иногда удаётся наблюдать такие же круги вокруг полной Луны. Ночью зимой в метель видны светящиеся вертикальные столбы от уличных фонарей, при этом сам фонарь находится в середине этого светящегося столба. И этот столб света виден даже в том случае, если сам фонарь заслонён от наблюдателя какой-нибудь крышей дома. Что это за столбы? Вспомним опыт с дифракционной решёткой. Максимумы при этом располагались вдоль определённой прямой, перпендикулярной направлению штрихов решётки. В случае с метелью наблюдается аналогичная картина. Пролетающие в горизонтальном направлении снежинки действуют как штрихи дифракционной решётки, только между этими «штрихами» определённое расстояние не соблюдается и поэтому все максимумы как бы «размазаны» и представляют собой сплошные столбы белого цвета. В летнее время, когда воздух особенно чист, можно также наблюдать дифракцию света, когда Солнце садится за далёкую гору, виднеющуюся на горизонте. Когда солнечный диск скроется за гору, то некоторое время можно наблюдать, что край горы, расположенный над зашедшим солнечным диском как бы «блестит», как стеклянный. На самом деле никакого блеска, связанного с отражением или преломлением света нет. Здесь наблюдается явление дифракции света, т.е. свет огибает гору и наблюдателю кажется, что гора блестит. Подобных примеров можно привести множество.
