Решить финансовую задачу, используя модель комбинированных процентов

1. Капитал был вложен в банк на 14 месяцев по 10 % годовых, начисляемых по комбинированной процентной ставке. Доход, полученный за год, составил 15000 рублей. Определить первоначальный капитал, вложенный в банк.

2. Какой величины достигнет долг, равный 30 000 руб, через 4,6 года при росте по сложной ставке наращения 18,5% годовых.

3. Сумма 18 000 рублей выплачивается через 3,8 года. Номинальная ставка процентов 18,0 % годовых. Определить первоначальную стоимость.

4. Сумма 2000000 рублей взята в долг на 4,8 года с годовой процентной ставкой 10% при условии погашения долга одним платежом в конце срока. Какую сумму нужно будет возвратить кредитору?

5. Сумма 4000000 рублей взята в долг на 2,5 года с годовой процентной ставкой 15% при условии погашения долга одним платежом в конце срока. Какую сумму нужно будет возвратить кредитору?

6. Сумма 4000000 рублей взята в долг на 4,2 года с годовой процентной ставкой 10% при условии погашения долга одним платежом в конце срока. Какую сумму нужно будет возвратить кредитору, если расчет производится по схеме комбинированных процентов?

7. Ссуда в размере 9000 руб выдана на срок 1,6 года под 14% годовых . Определить проценты и наращенную сумму. Насколько измениться эта сумма, если расчет будет по ставке наращения 14 % годовых?

8. Определить первоначальную стоимость 38000 рублей, выплачиваемой через 1,8 года. Процентная ставка наращения 12%.

9. Сумма 18 000 рублей выплачивается через 3,8 года. Ставка процентов 18,5 % годовых. Определить современную стоимость при комбинированном начислении процентов.

10. Какой платеж должен сделать заемщик, если он занял сумму 2200 рублей на 22 месяца под 6 % годовых?

11. Капитал был вложен в банк на 18 месяцев под 10 % годовых, начисляемых по комбинированной процентной ставке. Доход, полученный за год, составил 12000 рублей. Определить первоначальный капитал, вложенный в банк.

II. Применение модели дисконтирования.

Различают 2 вида дисконтирования – математическое и банковское. Если объявлена ставка дисконтирования d, то дисконтированная величина (начальная, современная) вычисляется по формуле: 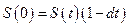. Это банковское дисконтирование. Оно применяется в банковских расчетах при покупке (учете) банковских краткосрочных операций – векселей и облигаций.

При математическом дисконтировании первоначальная денежная величина определяется по известной наращенной и заданной ставке наращения 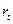. Так как 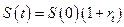, то первоначальная величина будет равна: 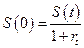. В зависимости от срока финансовой операции математическое и банковское дисконтирование бывает простым, сложным и комбинированным. Условия на срок tтакие же как при наращении. Математическое дисконтирование решает задачу обратную наращению первоначальной денежной величины. Особенно часто дисконтирование применяется при учете (сдаче) векселей в банк. Вексель – это письменное денежное обязательство должника о возврате долга, форма и обращение векселя регулируется вексельным правом. Номинал векселя состоит из величины долга и процентов. Если владелец предъявляет вексель в банк в момент наступления срока платежа, то ему будет выплачен номинал, если раньше срока, то выплачиваемая сумма будет меньше номинала, а если позже указанного срока, то вступает в действие вексельное право.

1). Модель простого дисконтирования (простого дисконта).

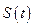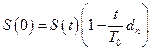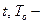А). проведем банковское дисконтирование. Дана ставка простого дисконта (простая учетная ставка), известен срок операции t,который меньше 1 года, наращенная величина . Тогда современная (первоначальная) величина будет равна: ; где срок и временная база, определенные по английской, французской или немецкой практикам. Если срок представлен в долях года, то .

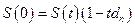Б). проведем математическое простое дисконтирование.

В этом случае величина первоначальная (современная) 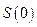выражается из формулы для расчета наращенной величины по модели простых процентов: .

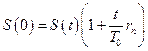Пример.

Владелец векселя на сумму 100000 рублей с уплатой 17.11 учел его в банке по учетной ставке 10% 20.08. определить сумму 1) выплаченную банком владельцу векселя; 2) дисконт банка. Для расчета использовать «германскую практику».

Решение.

Вексель сдан в банк раньше срока, поэтому владелец получит сумму, меньшую, чем номинал векселя. Срок, на который владелец сдает раньше вексель меньше года; поэтому применяем простое банковское дисконтировани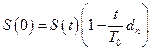е: , где 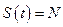- номинал векселя, 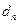- простая учетная ставка, t– срок, 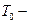временная база.

Определим срок по «германской практике»: количество дней в каждом месяце – 30 дней, а 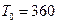дней.

Вычислим срок, на который вексель сдан (учтен) в банк раньше. Определим количество дней в августе: 30-19=11 дней. В сентябре таких дней будет 30, в октябре тоже 30, а в ноябре – 11. Общий срок составит: t=11+30+11+30-1=81 день. Как и раньше срок уменьшаем на 1 день, так как первый и последний день принимаем за один. Вычисляем сумму, выплаченную владельцу: 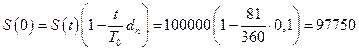рублей. Дисконт банка составит 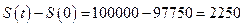рублей.

Пример.

Через 160 дней должник уплатит 10000 рублей. Ссуда была выдана под простые проценты 20% годовых. Какова первоначальная сумма и дисконт, если временная база а) 360 дней; б) 365 дней.

Решение.

В задаче дана ставка простых процентов, поэтому применяем математическое дисконтировани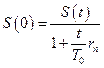е: , где 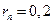- ставка простых процентов, t=160 дней – срок, 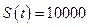руб – наращенная сумма долга. Тогда: 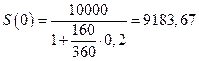рублей.

Дисконт банка: 10000-9193,95=806,05 рублей.

2). Модель сложного дисконтирования.

При использовании этой модели сложная учетная ставка применяется к дисконтированной на предыдущем шаге сумме. Поэтому в случае банковского дисконтирования имеем: 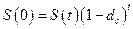, где t– срок (обычно целый срок в годах), 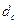- сложная учетная (дисконтная) ставка.

Пример.

Вексель на сумму 40000 рублей, срок платежа по которому наступает через 2 года учтен в банке по учетной ставке 20%. Найти сумму, полученную владельцем при учете(сдаче) векселя и дисконт банка при ежегодном дисконтировании.

Решение.

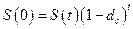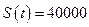Применим модель для сложного банковского дисконтирования: , где руб., 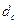=0,2; t= 2 года.

Проведем вычисления: 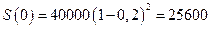руб. дисконт банка при этом будет: 40000-25600=14400 руб.

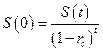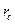Если же проводится сложное математическое дисконтирование, то значение первоначальной денежной величины выражается из формулы для сложных процентов: , где - ставка сложных процентов.

Пример.

Какая сумма была реально выдана, если владелец сдал вексель через 2 года в срок и получил 250000 рублей, если ставка сложных процентов равна 25 % годовых?

Решение.

Применим математическое дисконтирование по ставке сложных процентов: 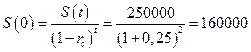рублей.

С помощью операций наращения и дисконтирования проводят сравнение денежных величин во времени. Для этого эти величины надо привести к одному моменту времени, то есть либо провести наращение, либо дисконтирование.

Пример.

Какая сумма больше 1500 у.е. сейчас или 1540 у.е через 0,5 года? Если сложная процентная ставка равна 10%?

Решение.

Обозначим 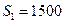у.е, 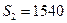у.е. приведем денежные суммы к одному моменту времени. Для этого надо произвести или наращение 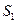или дисконтирование 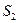на начальный момент времени. В задаче дана ставка сложных процентов, поэтому удобнее провести наращение 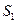в течение 0,5 года: 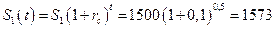у.е. сравним 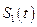и 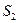. 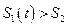, поэтому сейчас сумма 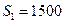у.е. больше, чем 1540 у.е. через полгода.

Пример.

Какая сумма больше 1500 у.е. сейчас или 1540 у.е через 0,5 года? Если простая учетная ставка равна 10% годовых?

Решение.

Обозначим 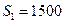у.е, 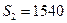у.е. в задаче дана ставка дисконтирования, поэтому удобнее провести дисконтирование 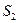и сравнить ее дисконтированную величину с 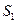на начальный момент времени. Проведем простое банковское дисконтирование. 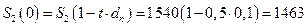у.е. , т.к. 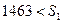, то 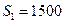у.е. больше, чем 1540 у.е. через 0,5 года.