Рабочая учебная программа курса
И методические указания к изучению предмета
Курс математики разбит на темы. По каждой теме указана литература, рекомендуемая для изучения и задачи для самостоятельного решения. Номера в скобках ( ) означают номер пособия из приведенного выше списка литературы. В каждой теме приведены методические рекомендации и вопросы для самопроверки. Темы объединены в разделы. После изучения раздела нужно выполнить очередную контрольную работу.
РАЗДЕЛ 1.
Векторы, аналитическая геометрия, комплексные числа.
ТЕМА 1. Векторы. ([1], гл.2, §4-§10); ([2], гл.9, §1-§8).
Векторы, линейные операции над ними.
Скалярное, векторное, смешанное произведения, их свойства и вычисление через координаты перемножаемых векторов.
Методические указания
Понятие вектора используется как в самой математике, так и в других дисциплинах: в механике, физике, электротехнике и др. Например, все основные действия над векторами соответствуют операциям над силами.
Изучая тему, выпишите определения коллинеарных, равных, компланарных векторов, определения скалярного, векторного, смешанного произведений. Научитесь вычислять скалярное, векторное, смешанное произведения по координатам перемножаемых векторов.
Вопросы для самопроверки
1. Определение вектора. Линейные операции над векторами.
2. Координаты вектора.
3. Определение скалярного произведения двух векторов, его свойства, выражение через координаты перемножаемых векторов.
4. Формула длины вектора, угла между двумя векторами, формула расстояния между двумя точками в декартовой системе координат.
5. Определение векторного произведения двух векторов, его свойства, выражение через координаты перемножаемых векторов.
6. Определение смешанного произведения трёх векторов, его свойства, выражение через координаты перемножаемых векторов.
ТЕМА2. Аналитическая геометрия.([1], гл.4, §18-24); .([2], гл.3, §6-7; гл.9, §11-§14).
Прямая на плоскости, различные формы её уравнения.
Взаимное расположение прямых.
Методические указания
В аналитической геометрии изучение фигур на плоскости производится с помощью их уравнений. В декартовой системе координат на плоскости уравнения вида Ax+By+C=0 или Y=kX+b определяют некоторую прямую.
Вопросы для самопроверки
1. Определение линий в аналитической геометрии.
2. Виды уравнений прямой на плоскости.
ТЕМА 3. Комплексные числа.( [1], гл. 3, §12-17, стр.78-117, [2], гл. 14, §6); ([3] стр.145 № 1, 3, 5, 20, 22, 29, 34, 43).
Комплексные числа, действия над ними.
Тригонометрическая и показательная форма комплексного числа.
Методические указания
Наибольшие трудности вызывает тригонометрическая форма записи комплексного числа. Чтобы не сделать ошибку при определении аргумента комплексного числа, изображайте число в виде вектора на комплексной плоскости.
Вопросы для самопроверки
1. Определение комплексного числа. Изображение его на комплексной плоскости.
2. Действия над комплексными числами в алгебраической форме.
3. Тригонометрическая форма комплексного числа. Действия над комплексными числами в тригонометрической форме.
4. Показательная форма комплексного числа. Формула Эйлера.
РАЗДЕЛ 2.
Введение в математический анализ.
Дифференциальное исчисление функции одной переменной.
ТЕМА 4. Введение в математический анализ.([1], гл.6, §29-§32); ([2], гл.2, гл. 4).Функция. Обзор элементарных функций.
Числовая последовательность, её предел. Бесконечно малые и бесконечно большие величины.
Теоремы о пределах. Замечательные пределы. Сравнение бесконечно малых.
Непрерывность функций. Точки разрыва. Непрерывность основных элементарных функций. Свойства функций, непрерывных на отрезке.
Методические указания
Понятие предела одно из наиболее важных и трудных в математическом анализе. Определение предела функции в точке и в бесконечности сопровождайте рисунком. Типы точек разрыва также иллюстрируйте графически. Чтобы освоить технику вычисления пределов, разберите примеры, решённые в задачниках (2), (3). Обратите внимание, какие пределы вычисляются на основе двух «замечательных» пределов.
Вопросы для самопроверки
1. Определение предела последовательности.
2. Определение предела функции при х→а и при х→∞.
3. Понятие бесконечно малой и бесконечно большой. Примеры.
4. Основные теоремы о пределах.
5. Первый и второй замечательные пределы.
6. Определение непрерывности функции в точке и на отрезке. Точки разрыва. Непрерывность элементарных функций.
ТЕМА 5. Дифференциальное исчисление функции одной переменной. ([1], гл.7); ([2],гл.5, гл.6).
Определение производной функции, её геометрический смысл. Непрерывность функции, имеющей производную. Производная суммы, произведения и частного функций.
Производная сложной и обратной функции. Таблица производных.
Дифференциал функции, его геометрический смысл.
Исследование функций: условия возрастания и убывания функций, экстремум, выпуклость и вогнутость, точки перегиба, асимптоты.
Методические указания
Выучите наизусть таблицу производных основных элементарных функций. Умение находить производные сложных функций необходимо для успешной сдачи экзамена и дальнейшего изучения высшей математики.
При изучении темы "экстремум функции" довольно распространённой ошибкой является использование необходимого условия экстремума вместо достаточного. На самом деле обращение в некоторой точке производной в нуль не является достаточным условием наличия в этой точке экстремума. Например, производная функции у=x  равна нулю в точке х=0, но в этой точке функция не имеет экстремума.
равна нулю в точке х=0, но в этой точке функция не имеет экстремума.
Вопросы для самопроверки
1. Определение производной. Её геометрический смысл, её механический смысл.
2. Производная суммы, произведения, частного.
3. Производная сложной функции.
4. Таблица производных основных элементарных функций.
5. Определения возрастающей и убывающей на отрезке функции. Достаточные признаки возрастания и убывания.
6. Определения точки максимума и точки минимума функции. Экстремум. Необходимое условие экстремума. Достаточные условия экстремума.
РАЗДЕЛ 3
Неопределённый и определённый интегралы
ТЕМА 6.Интегральное исчисление функции одной переменной. ([1], гл.8, гл.9); ([2],гл.7, гл.8 ).
Первообразная. Неопределённый интеграл, его свойства. Таблица интегралов. Основные методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.
Разложение рациональных дробей на сумму простейших. Интегрирование рациональных дробей.
Интегрирование иррациональных и тригонометрических выражений.
Определение определённого интеграла, его свойства.
Формула Ньютона - Лейбница.
Замена переменной и интегрирование по частям в определённом интеграле.
Геометрические и физические приложения определённого интеграла.
Несобственные интегралы на конечном и бесконечном интервалах.
Методические указания
Выпишите таблицу основных формул интегрирования. На примерах разберите метод подстановки и метод интегрирования по частям.
Важно понять определение определённого интеграла как предела интегральной суммы и вытекающие из него приложения к геометрическим и физическим задачам.
Вопросы для самопроверки
1. Определение первообразной и неопределённого интеграла. Свойства неопределённого интеграла.
2. Таблица основных интегралов.
3. Замена переменной в неопределённом интеграле.
4. Метод интегрирования по частям.
5.Определение определённого интеграла. Его геометрический смысл и свойства.
6.Формула Ньютона- Лейбница.
7.Вычисление площадей, длин дуг, объёмов с помощью определённого интеграла.
8.Несобственные интегралы первого и второго рода. Сходимость и расходимость.
РАЗДЕЛ 4
Тема 7.Обыкновенные дифференциальные уравнения.([1], гл.10, §57-64)
1. Физические задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка. Задача Коши. Частное и общее решения.
2. Дифференциальные уравнения первого порядка с разделяющимися переменными. Однородные и линейные уравнения первого порядка. Уравнение Бернулли.
3. Линейные дифференциальные уравнения, однородные и неоднородные. Структура общего решения.
4. Линейные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
Методические указания
1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Уравнение, в котором содержится независимая переменная, искомая функция и её производные или дифференциалы, называется обыкновенным дифференциальным уравнением.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в это уравнение.
Дифференциальное уравнение первого порядка имеет вид: F (х, y, y') = 0 (уравнение первого порядка в неявной форме), или y ' = f (х, y) ( уравнение первого порядка, разрешённое относительно производной), или
P(х, y) • dx + Q(х, y) • dy = 0 (дифференциальная форма).
Решением дифференциального уравнения называется функция, при подстановке которой в уравнение получается тождество.
Решение дифференциального уравнения называется общим решением, если оно содержит столько независимых произвольных постоянных, каков порядок уравнения.
Общее решение дифференциального уравнения первого порядка имеет вид y = 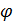 ( х, C), оно зависит от одной произвольной постоянной С и является решением уравнения при любом допустимом С.
( х, C), оно зависит от одной произвольной постоянной С и является решением уравнения при любом допустимом С.
Частным решением дифференциального уравнения первого порядка называется решение, получаемое из общего решения при каком - либо определённом значении произвольной постоянной С.
Соотношение вида Ф(х, y, C)=0, неявно определяющее общее решение, называется общим интегралом дифференциального уравнения первого порядка. Соотношение, получаемое из общего интеграла при конкретном значении постоянной С, называется частным интегралом дифференциального уравнения.
Задача нахождения частного решения по начальным условиям называется задачей Коши.
Задача Коши для дифференциального уравнения первого порядка ставится следующим образом:
Найти частное решение, удовлетворяющее начальному условию y (х0) = y0 , где х0, y0 заданные значения независимой переменной х и
искомой функции y.
График частного решения дифференциального уравнения называется интегральной кривой. Графиком общего решения является семейство интегральных кривых.
2. ОСНОВНЫЕ ТИПЫ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
2.1. УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ.
Дифференциальные уравнения с разделяющимися переменными могут быть записаны в виде:
У ' = f(х) • g(У) или М(х) • N(у) •dх + Р(х) Q( у) •dу = 0. Для решения такого уравнения надо обе его части умножить или разделить на такое выражение, чтобы в одну часть уравнения входило только х, а в другую только у и затем проинтегрировать обе части. При делении обеих частей уравнения на выражение, содержащее х и у, могут быть потеряны решения, обращающие это выражение в нуль.
Пример 1. Найти частное решение уравнения х • dх + у • dу = 0, удовлетворяющее начальному условию у(1) = 0 . Выделить интегральную кривую, проходящую через точку М (1,0).
Решение. Разделим переменные: х • dх = - у • dу. Интегрируем:
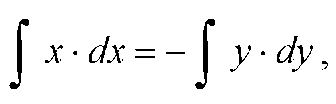 получаем
получаем 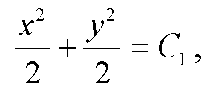 или, обозначив 2 С1
или, обозначив 2 С1
через С2, будем иметь х2 + у2 = С2 - общий интеграл. Это уравнение семейства концентрических окружностей с центром в начале координат
и радиуса С. Для решения задачи Коши подставим в общий интеграл
начальные условия х = 1, у = 0: 12 + 02 = С2 ,откуда
С2 = 1, а тогда искомое частное решение х2 + у2 = 1 (частный интеграл)- окружность с центром в начале координат радиуса 1. Это интегральная кривая, проходящая через точку М (1,0).
2.2.ОДНОРОДНЫЕ УРАВНЕНИЯ
Однородные уравнения могут быть записаны в виде:
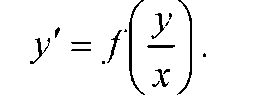
Для решения однородного дифференциального уравнения применяется подстановка u =  или y = u • x, где u - функция от x, подлежащая определению; при этом y' = u' x + u .
или y = u • x, где u - функция от x, подлежащая определению; при этом y' = u' x + u .
Пример 2. Найти общее решение (или общий интеграл) дифференциального уравнения:
(x 2 + y 2)dx–xydy = 0 .
Решение. Разделив обе части уравнения на dx, приведём его к виду
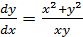 или
или 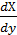 =
= 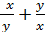
Применив подстановку у = uxу' = u'х + u, найдём:
u'х+ u = u +  .
.
Разделяем переменные и интегрируем:
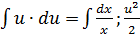 =ln│x│+C
=ln│x│+C
Учитывая, что u =  , получим:
, получим: 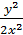 , = ln│х│ + C. Это - общий интеграл.
, = ln│х│ + C. Это - общий интеграл.
Кроме того, х = 0 - интеграл данного уравнения.
Ответ: 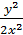 , = ln│х│ + C; х = 0
, = ln│х│ + C; х = 0
2.3 ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и её производной. Общий вид линейного уравнения
у' + P(х) • у = Q(х). Линейное уравнение сводится к двум уравнениям с разделяющимися переменными, если искомую функцию y заменить произведением двух вспомогательных функций. Полагаем y=u(x)-v(x), где и(х) и v(x) - неизвестные функции от х, одна из которых, например v(x), может быть выбрана произвольно. Подставляя в уравнение у = u • v, у' = u' • v + u • v', после преобразования получаем
u' • v + u • (v' + P(х) • v) = Q(х). (*)
Определяем v(х) из условия v' + P(х) • v = 0, выбирая в качестве v( х) одно из частных решений этого уравнения. Затем из уравнения (*) находим функцию и(х, С) и общее решение линейного уравнения
у=u(х, С)∙v(х).
Пример 3. Найти общее решение дифференциального уравнения
у' - у • ctgx = 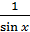
Решение. Ищем общее решение уравнения в виде у = u • v, тогда у' = u' • v + u • v' и данное уравнение примет вид
u' •v+u• (v' -v•ctgx) =—1—. (**)
sin x
Полагаемv’- v•ctgx = 0, откуда v’=v∙ctg x = v•ctgx, dv/v =ctgx • dx.
Интегрируя последнее уравнение, получаемv=sinx.Подставляяv=sinx
в уравнение (**), получим уравнение относительноu(x):
u’ •sinx=1/sinx.Интегрируя это уравнение, получаем u=- ctgx +C .
Итак, общее решение заданного уравнения имеет видy=uv=
=( - ctgx+C) sin x= - cosx+C sin x.
Ответ:y= - cosx+C sin x.
ЗАДАНИЯ КОНТРОЛЬНЫХ РАБОТ
ЗАДАНИЕ 1

Даны координаты точек:A, B, C.
Найти: 1) длину вектора 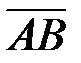 ,
,
2) угол между векторами 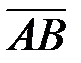 и
и 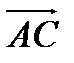 ,
,
3) уравнение прямой AB,
4) уравнение высоты, опущенной из вершины Cна сторону AB,
5) уравнение медианы, опущенной из вершины В на сторону АС,
6) сделать чертеж.
1.1 A (5, 1 ); B (-7, 6 ); C (3, -4 ).
1.2 A(5, 2 ); B(2, 5 ); C(1, 2 ).
1.3 A(-2, 0 ); B(-1, 7 ); C(4, -8).
1.4 A(2, -1 ); B(1, 2 ); C(3, 2 ).
1.5 A(-1, 2 ); B(4, -1 ); C(2, 1 ).
1.6 A(1, -1 ); B(-2, 0 ); C(2, 1 ).
1.7 A(1, 2 ); B(1, -1 ); C(0, 1 ).
1.8 A(1, 0 ); B(1, 2 ); C(2, -2 ).
1.9 A (1, 3 ); B (4, -1 ); C (3, 0 ).
1.10 A (0, 3 ); B (-1, 3 ); C (-2, 4 ).
ЗАДАНИЕ 2
Дано комплексное число 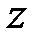 . Требуется:
. Требуется:
1) записать число 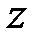 в алгебраической и тригонометрической формах;
в алгебраической и тригонометрической формах;
2) найти все значения 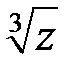 и изобразить их радиус-векторами;
и изобразить их радиус-векторами;
3) найти 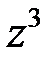 , ответ записать в тригонометрической и алгебраической формах.
, ответ записать в тригонометрической и алгебраической формах.
2.1 z= 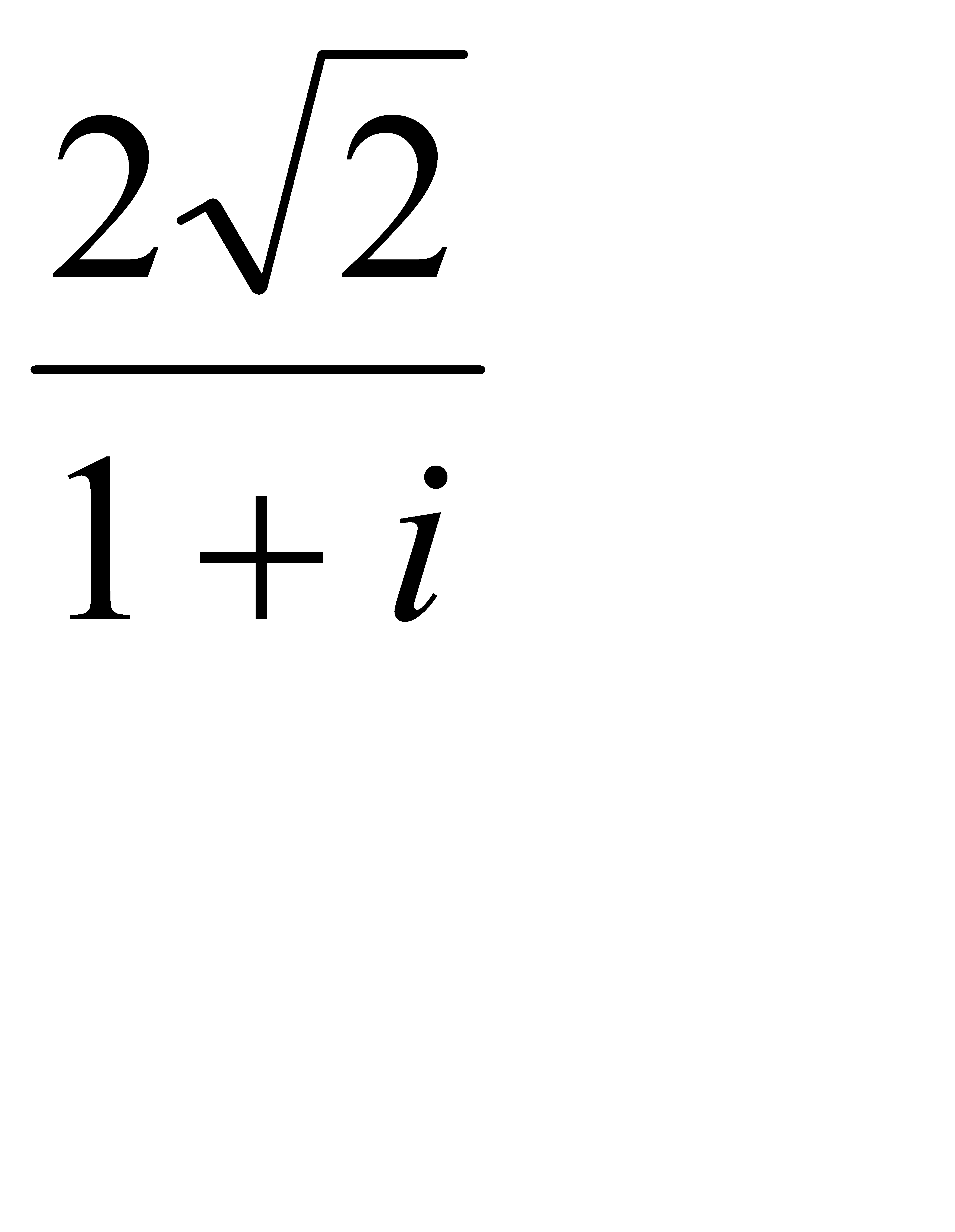 ;
;  2.2 z =
2.2 z = 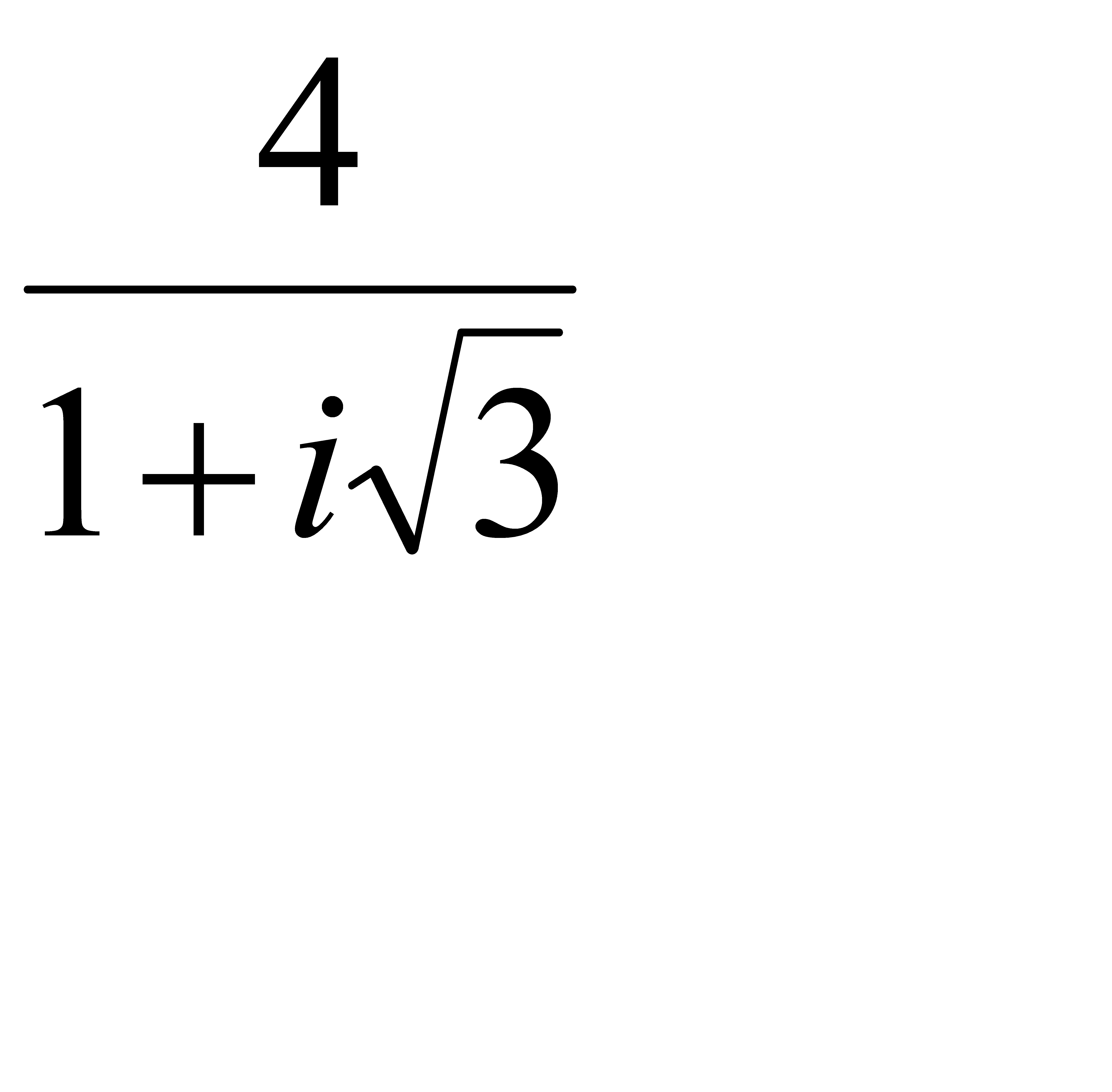 ;
;
2.3 z = – 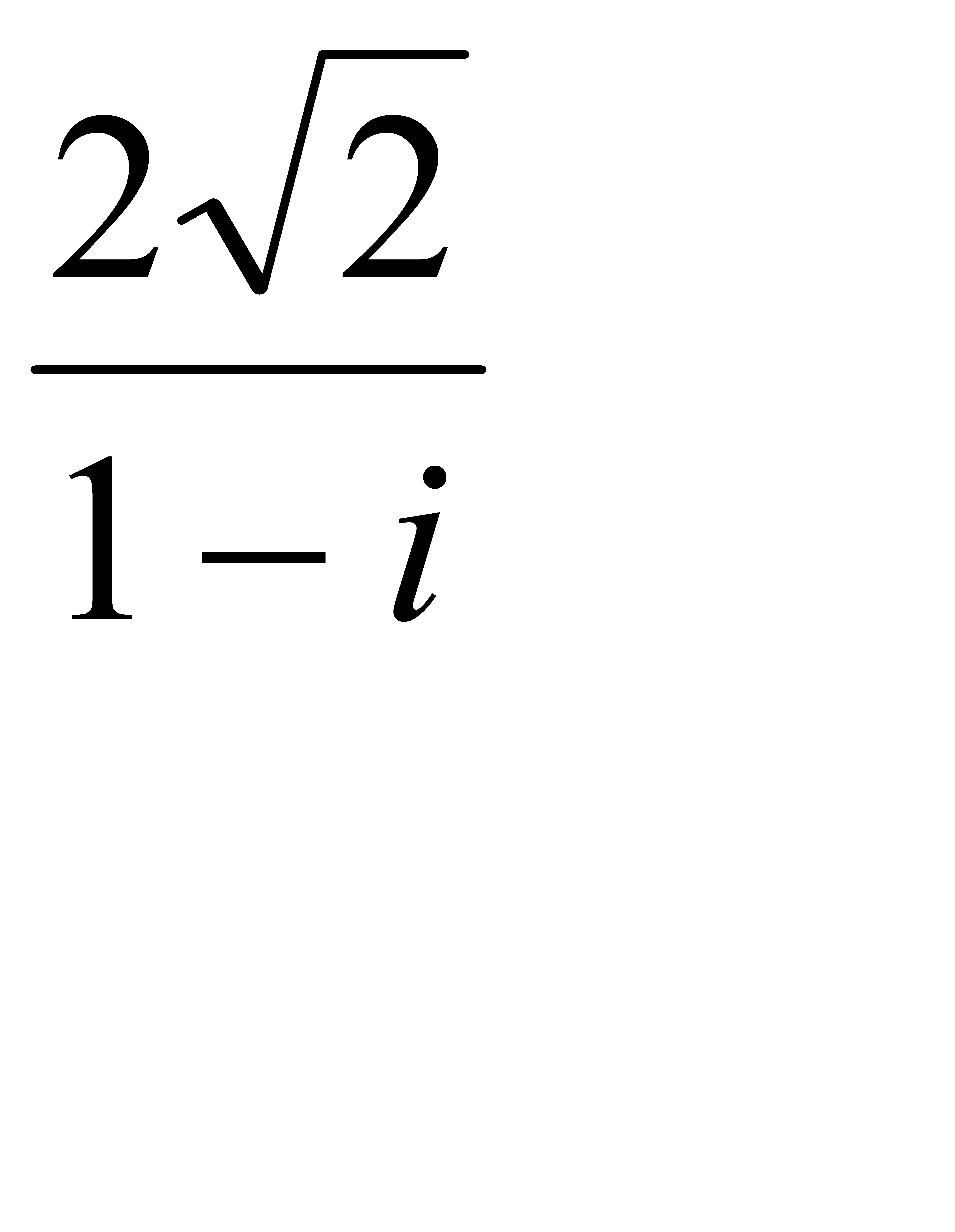 ;2.4 z = –
;2.4 z = – 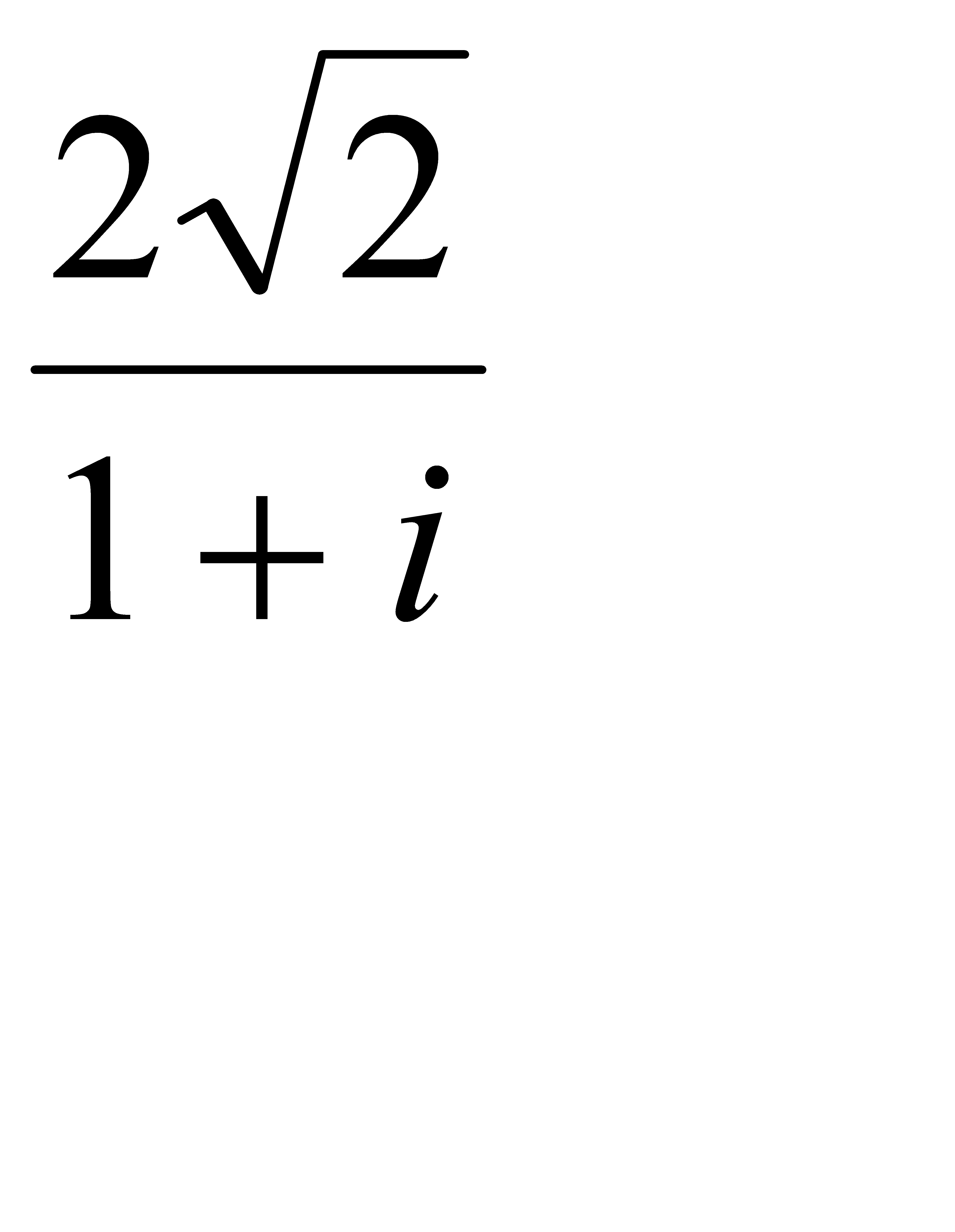 ;
;
2.5 z = 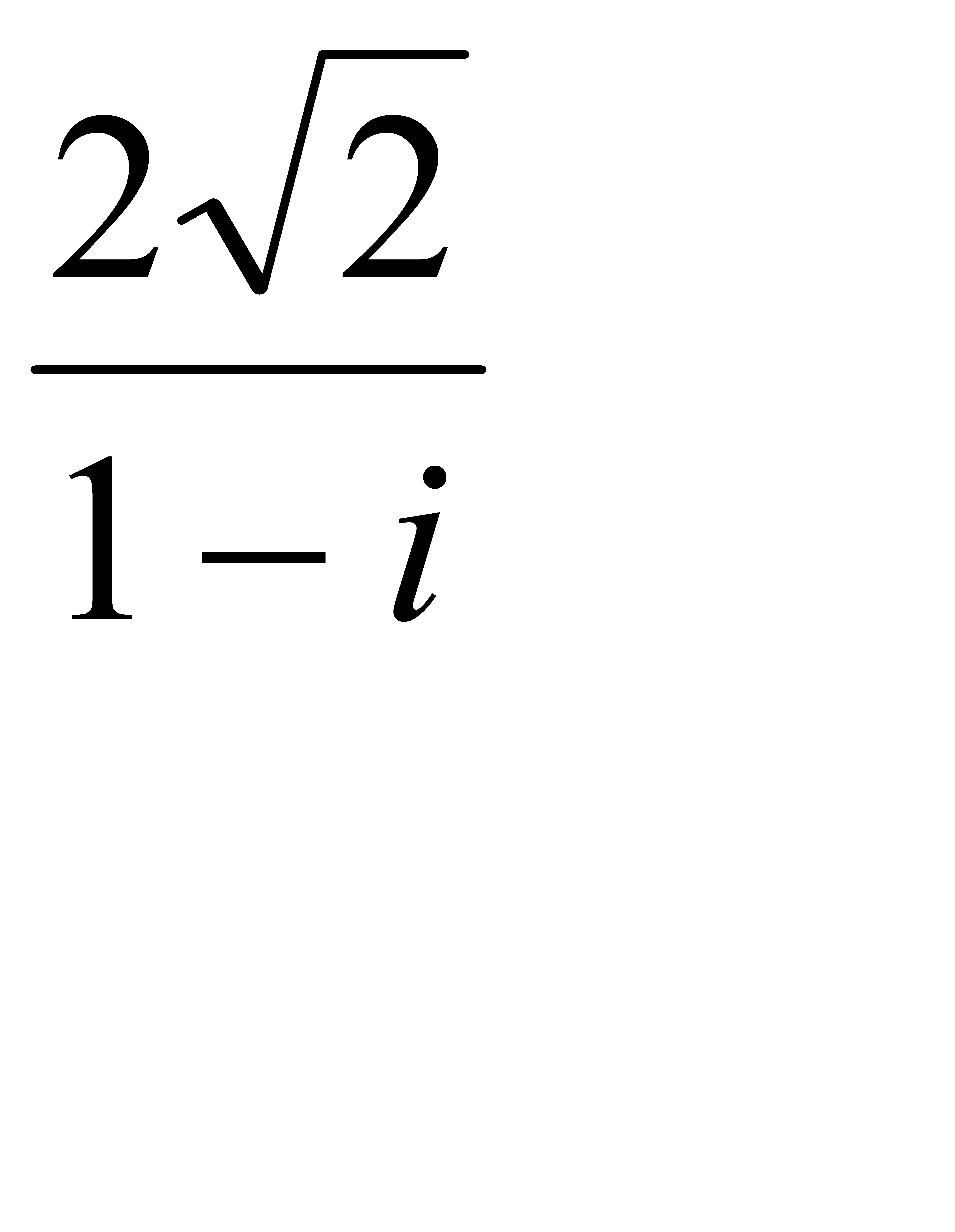 ; 2.6 z =
; 2.6 z = 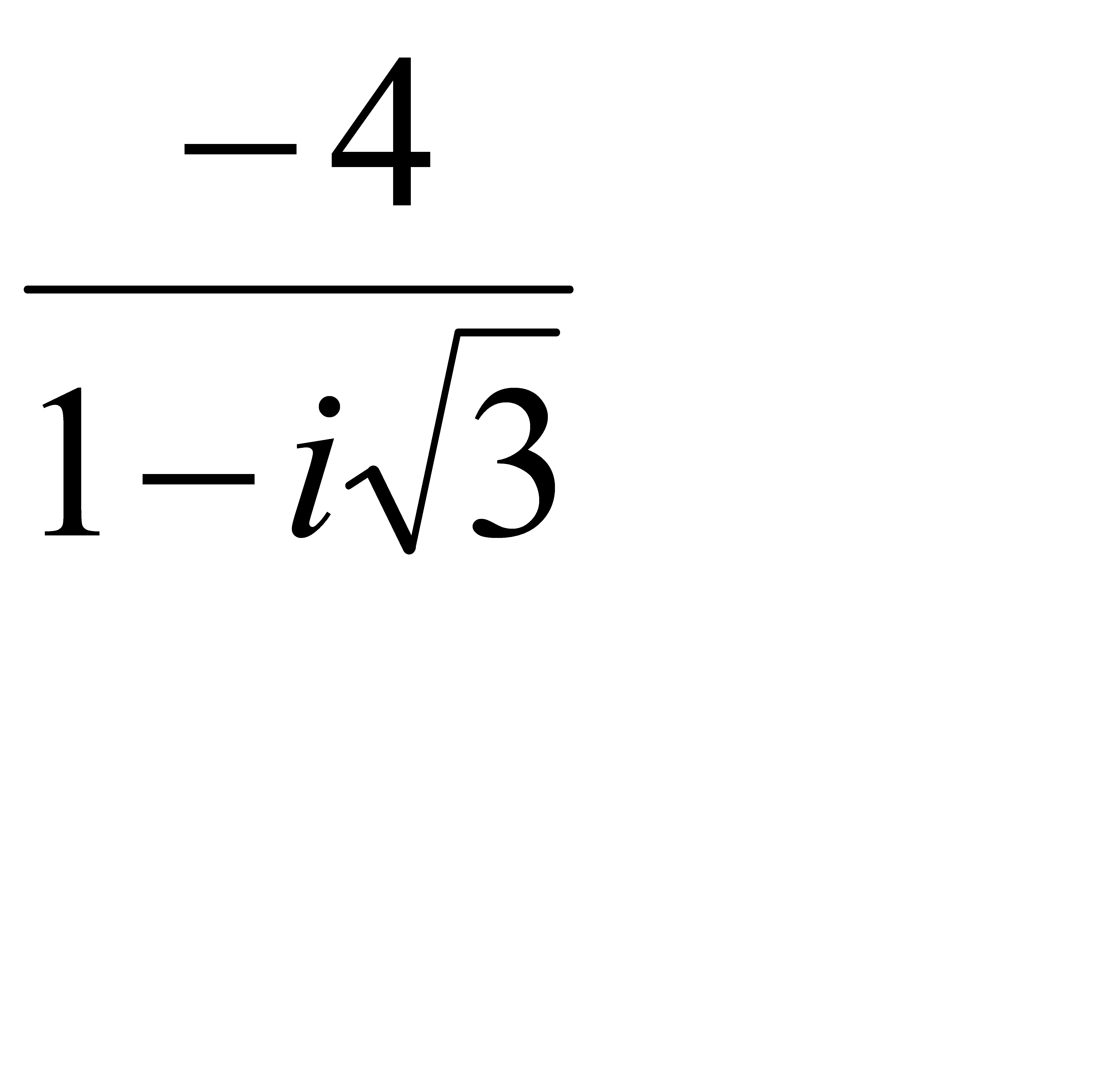 ;
;
2.7 z = 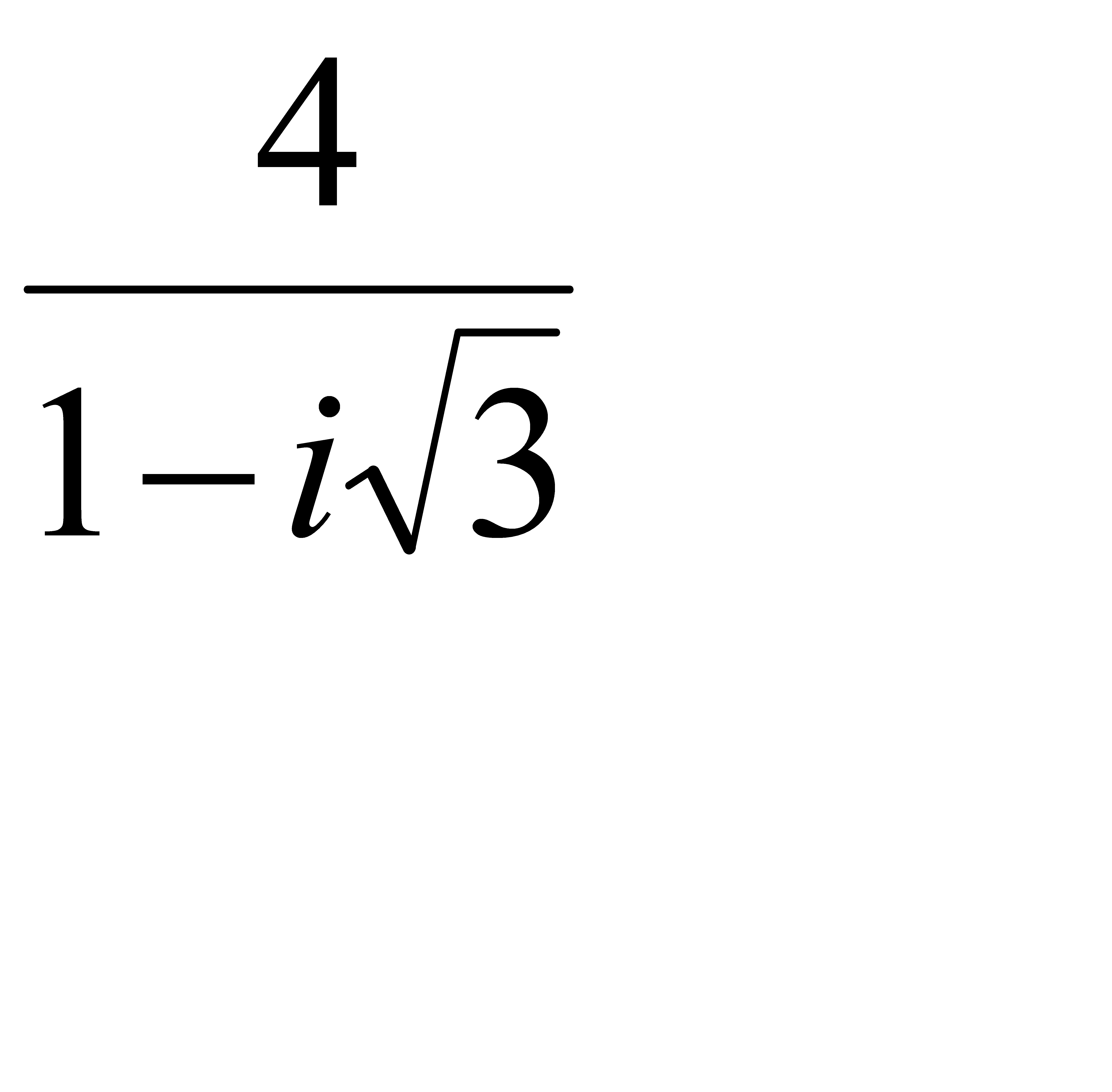 ; 2.8 z =
; 2.8 z = 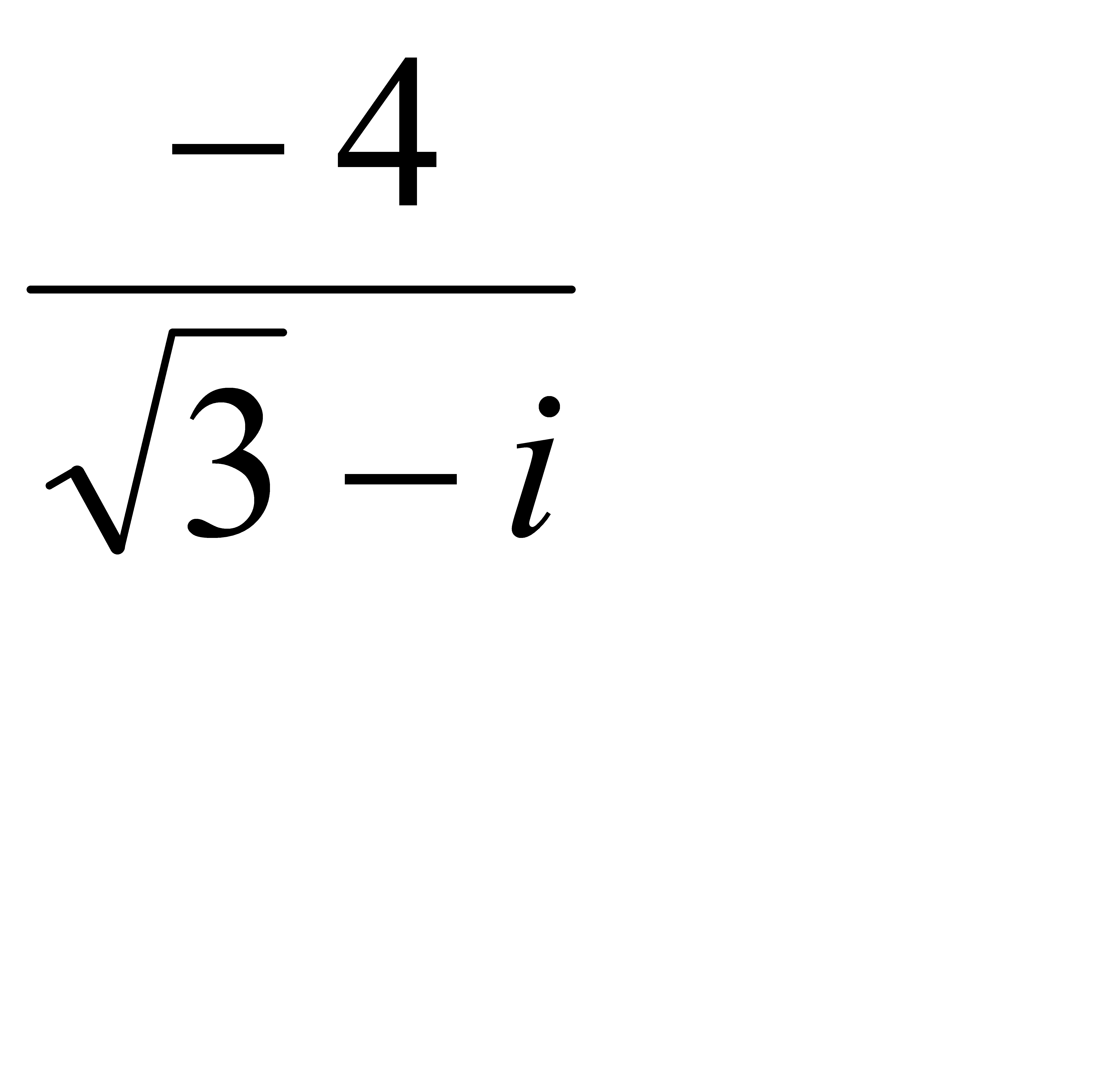 ;
;
2.9 z = 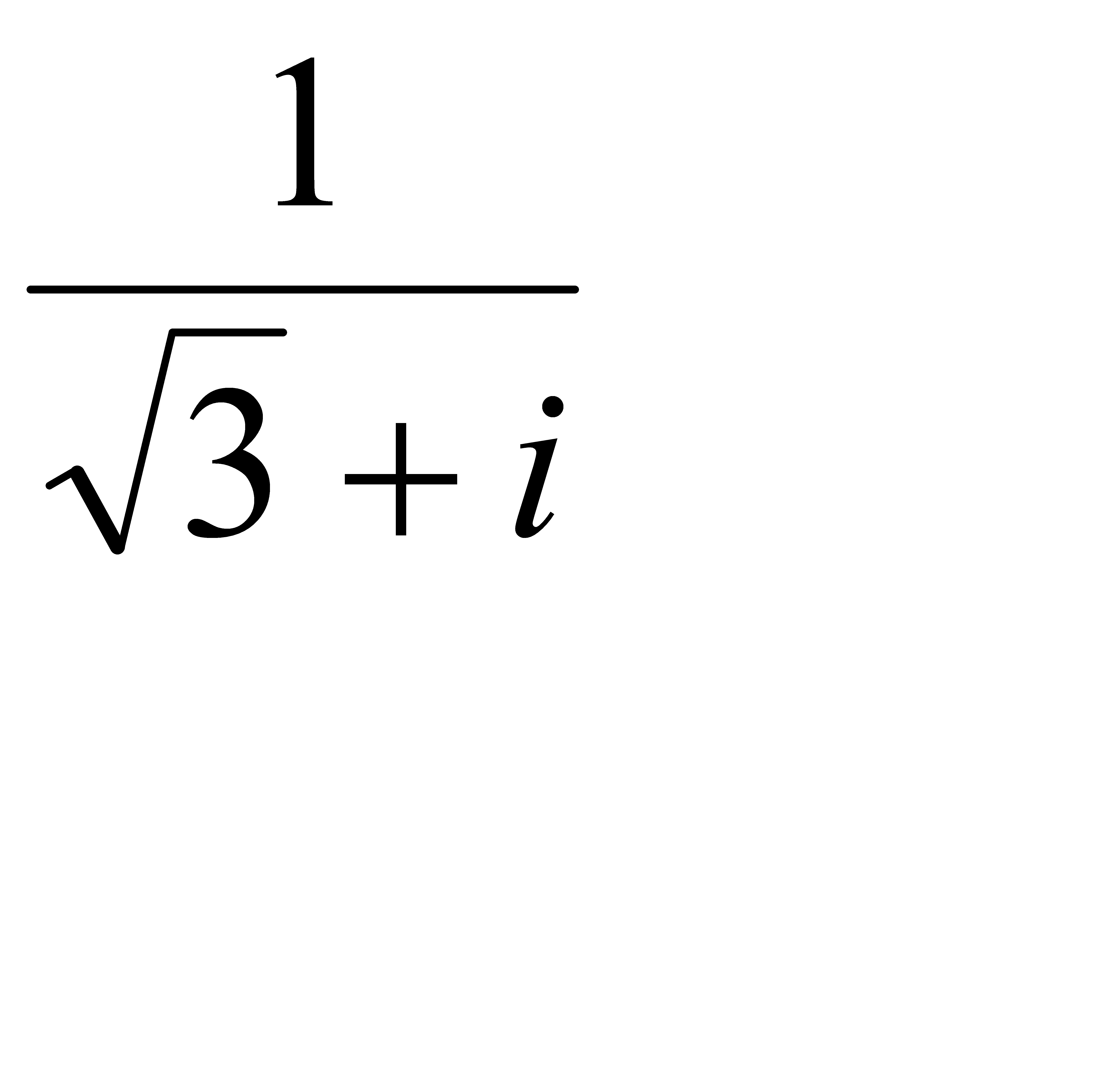 ; 2.10 z =
; 2.10 z = 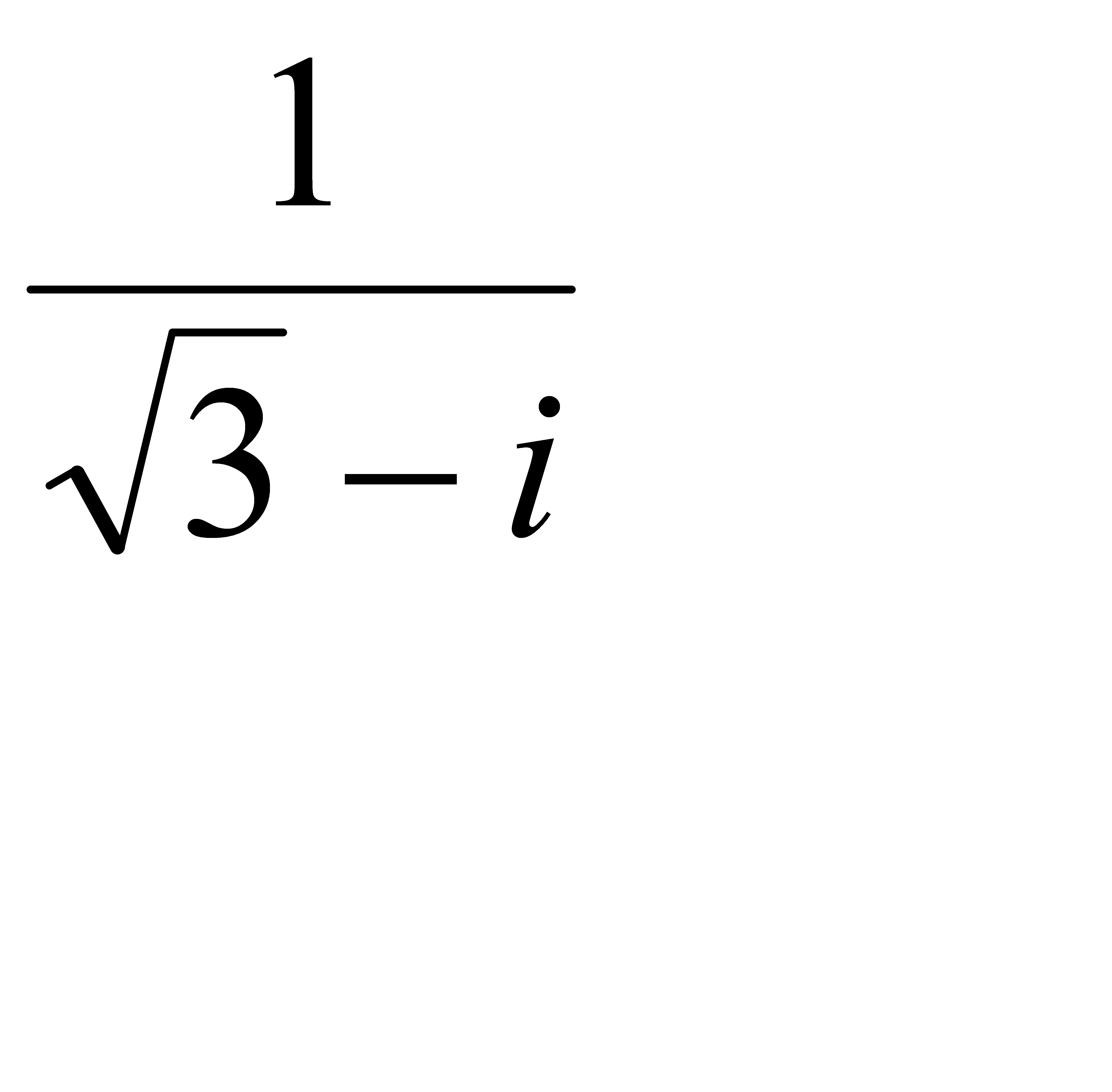 .
.
ЗАДАНИЕ 3
Найти пределы функций.
3.1 a) 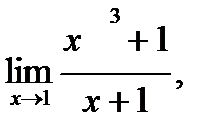 б)
б) 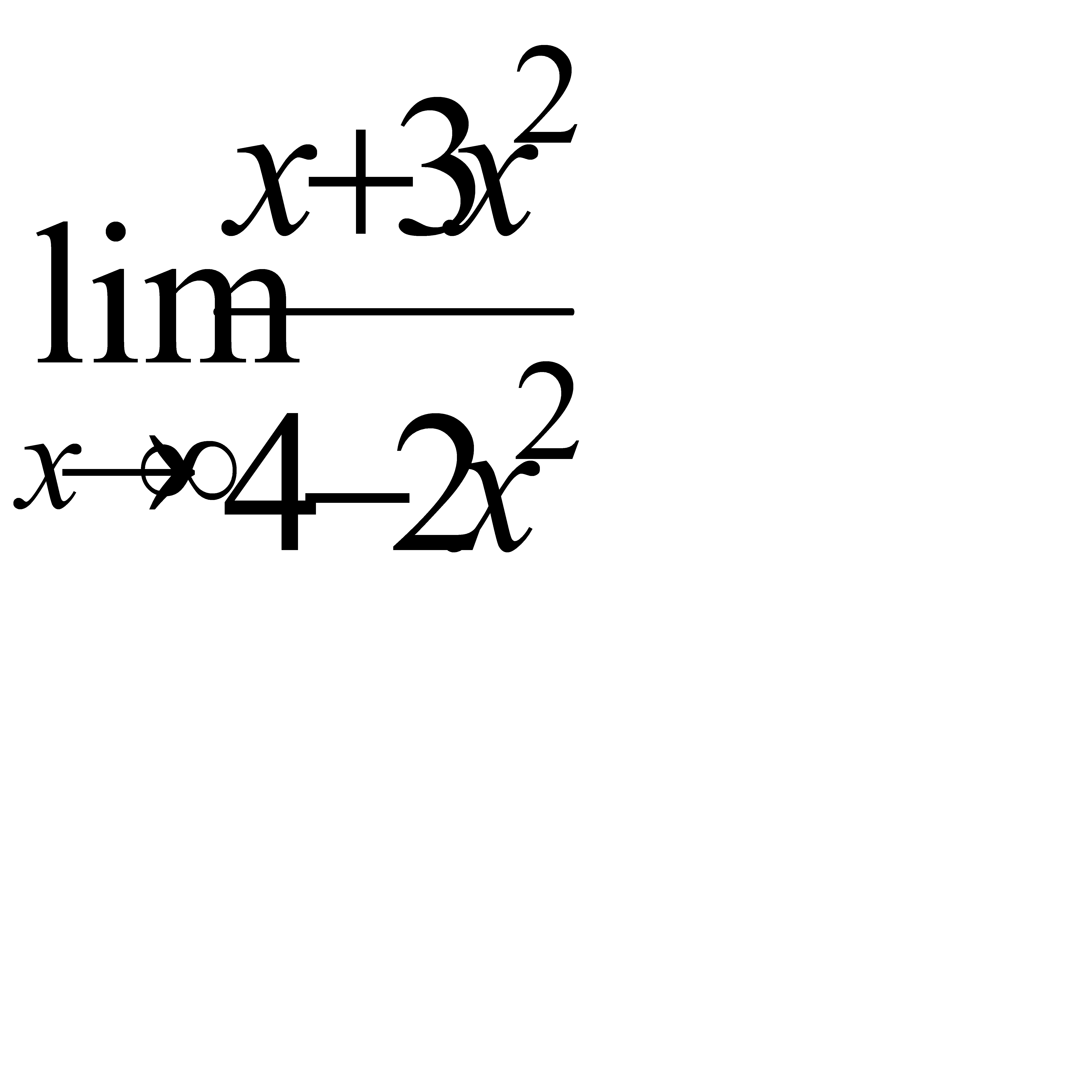 , в)
, в) 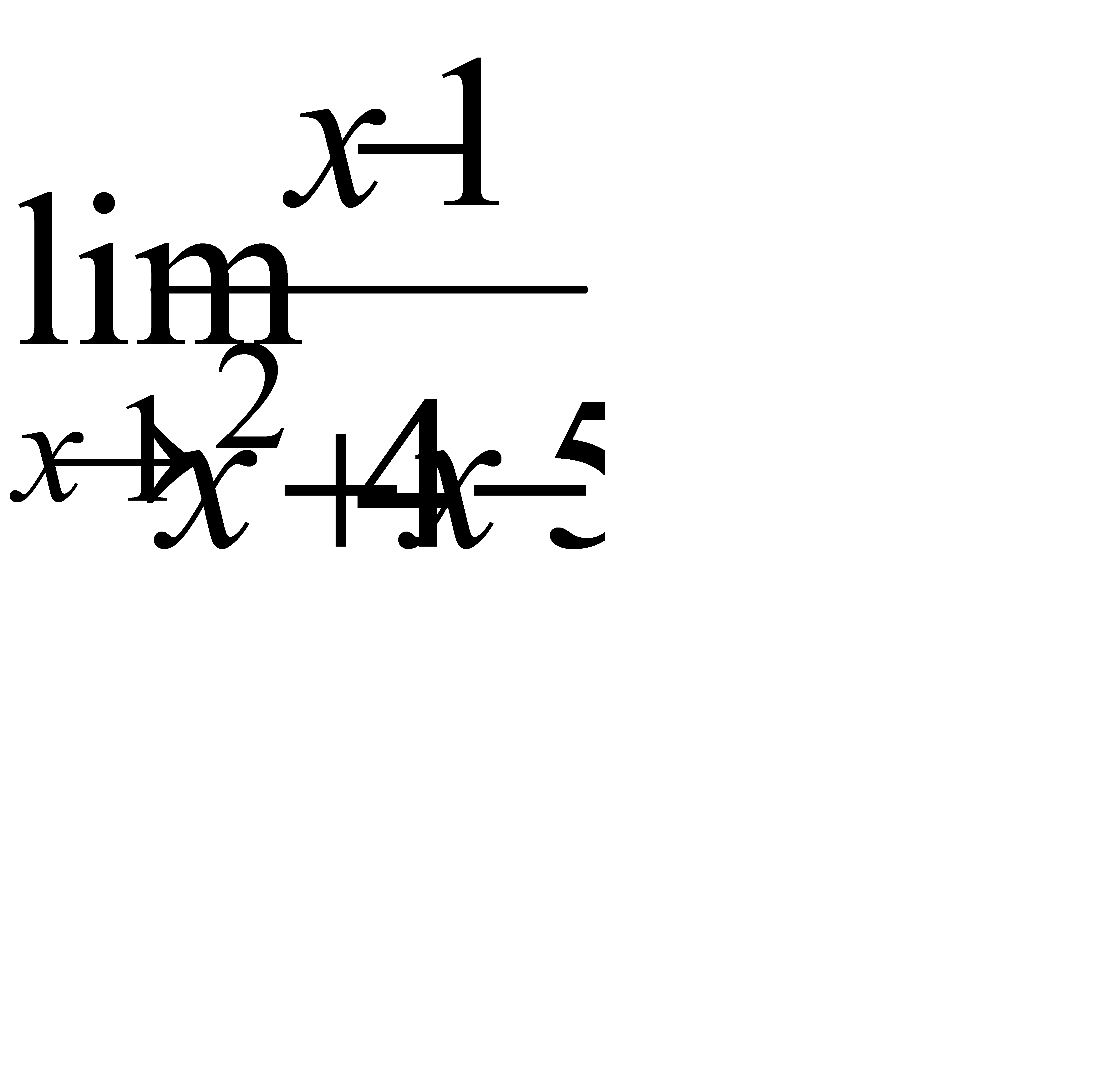 ,
,
г) 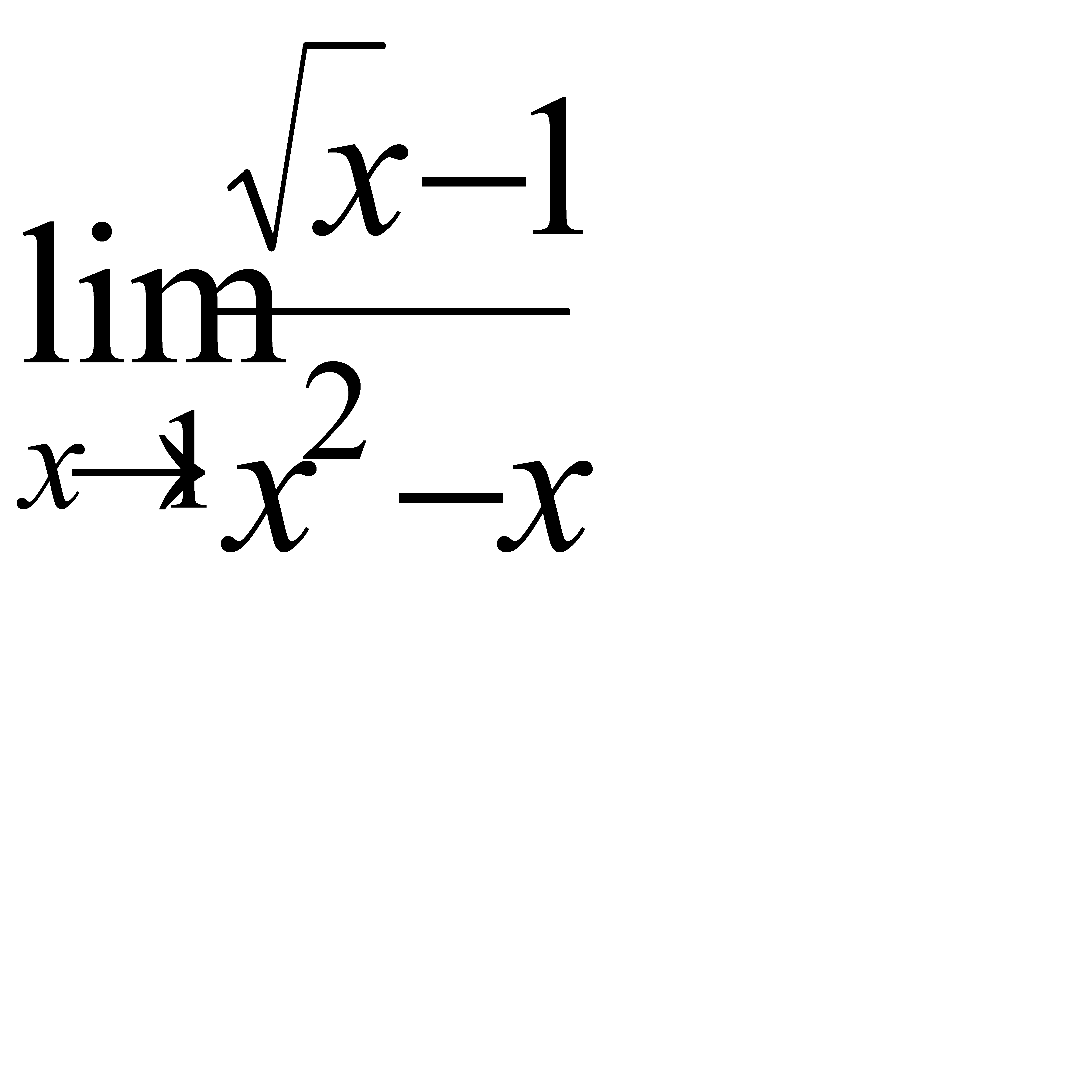 , д)
, д) 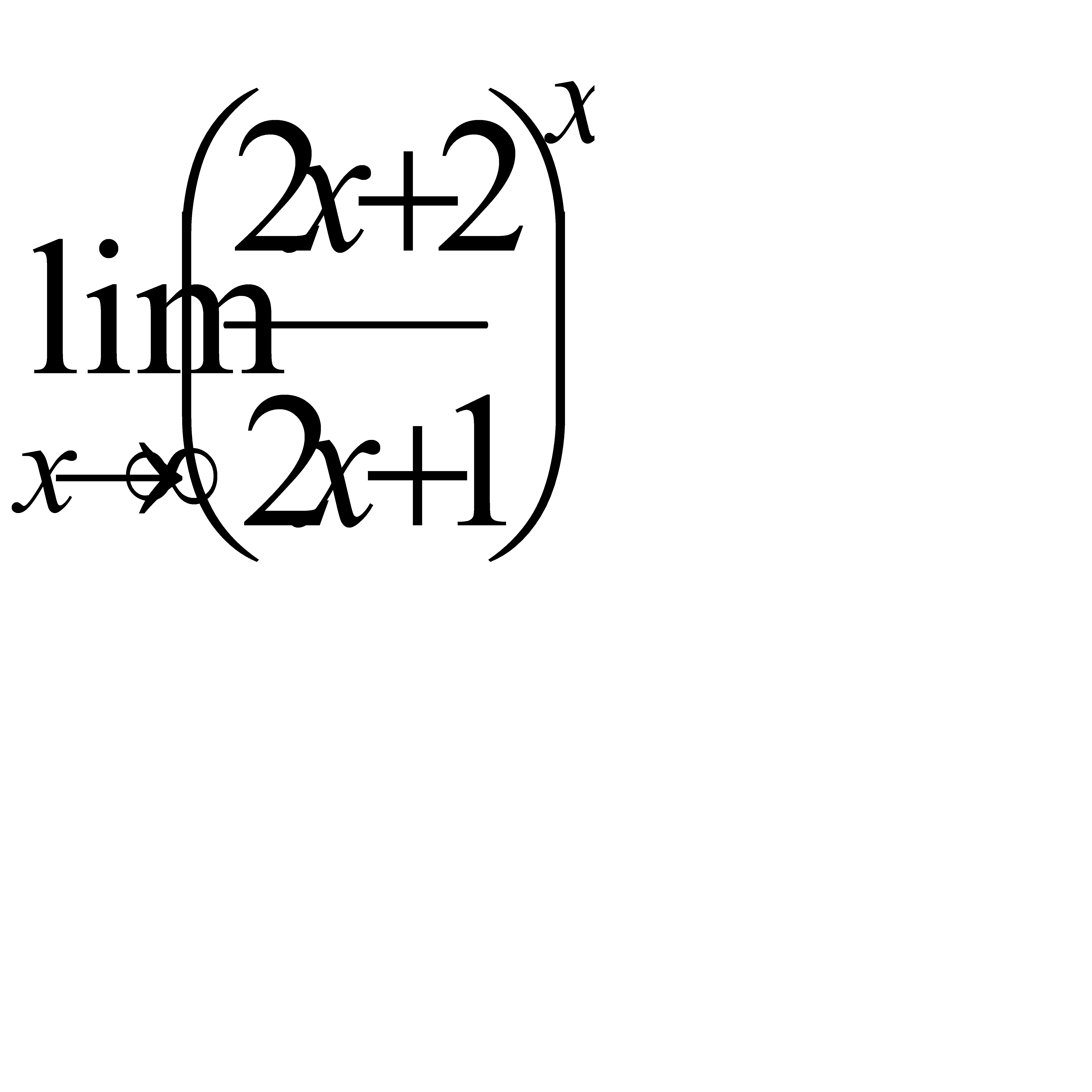
3.2 а) 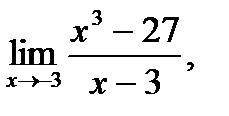 б)
б) 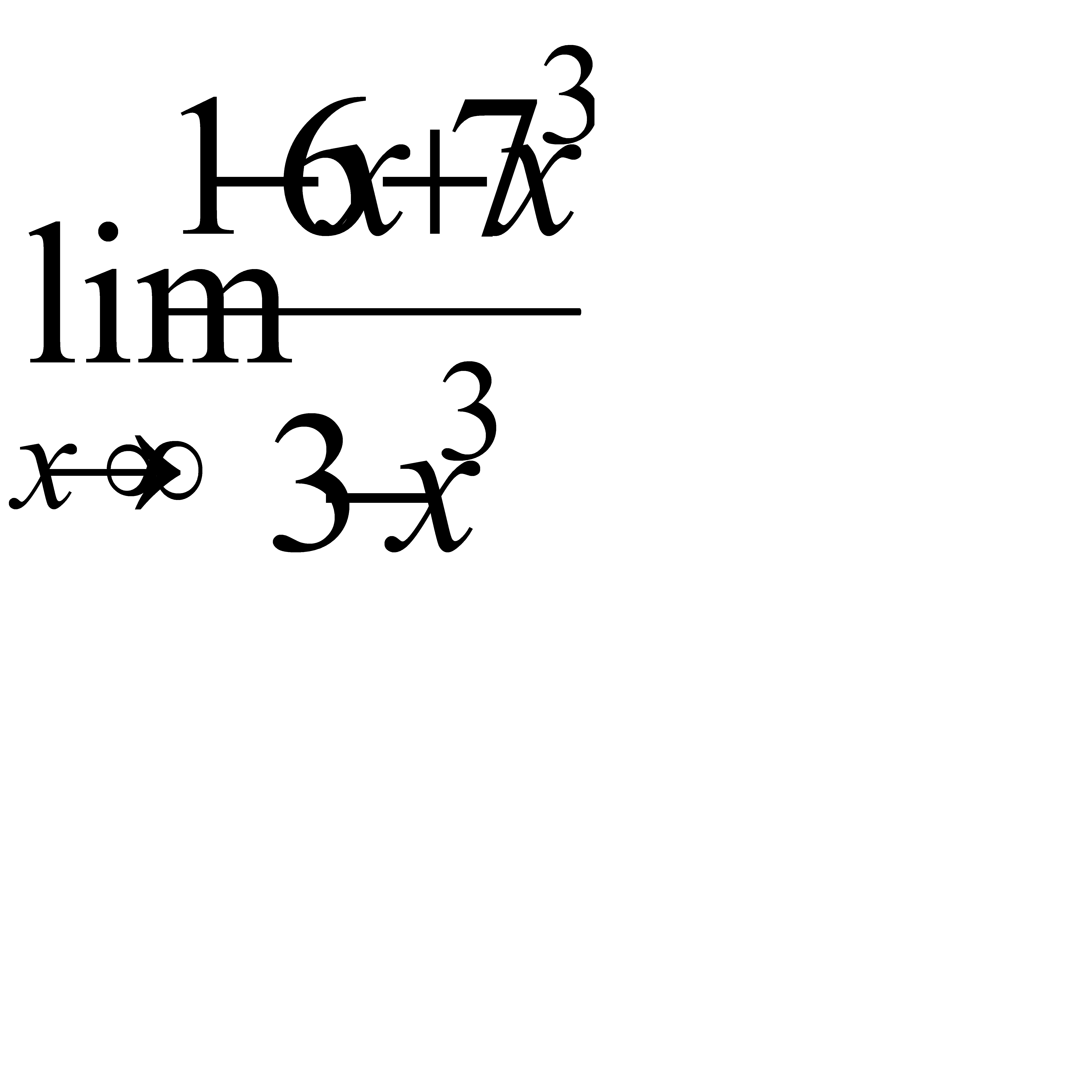 , в)
, в) 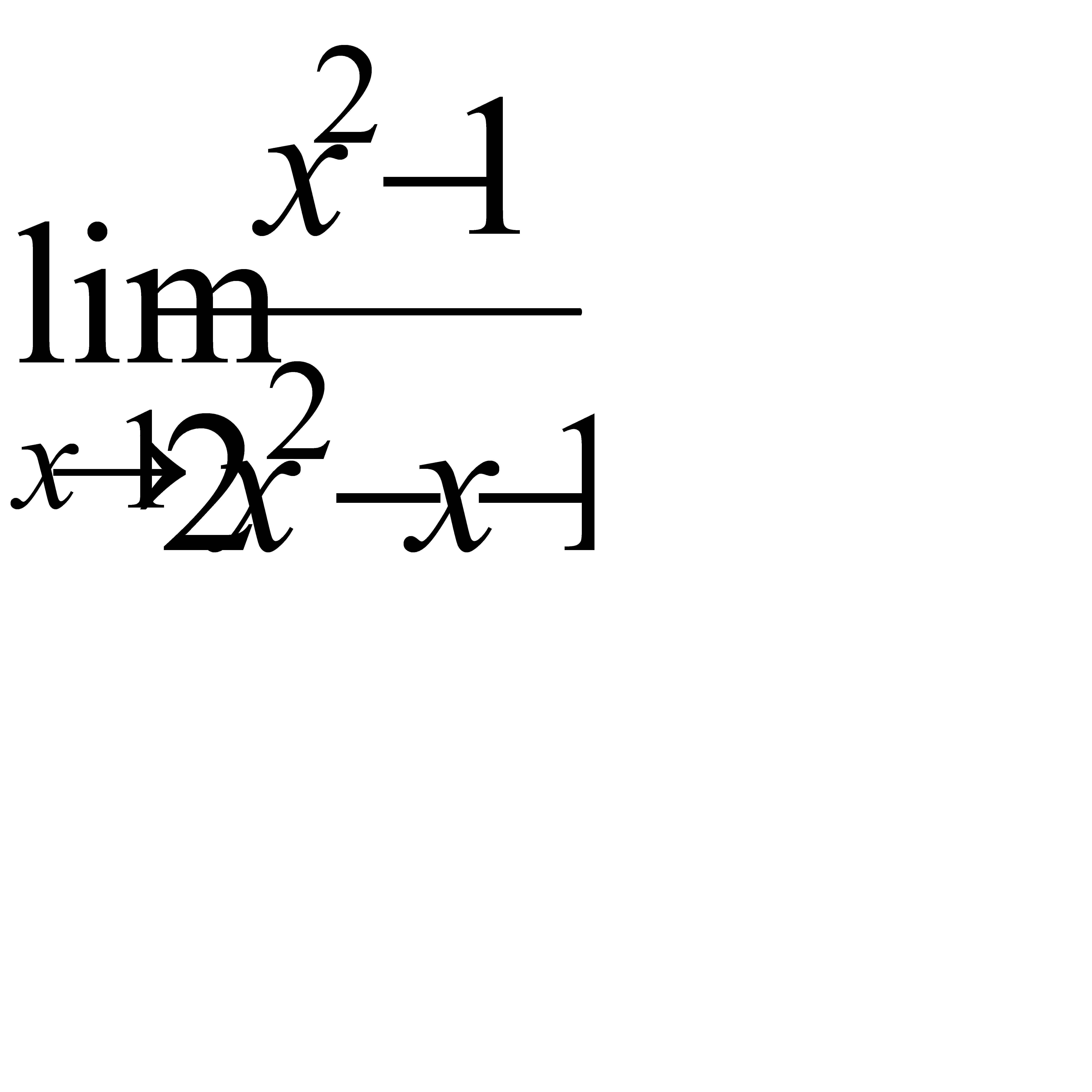 ,
,
г), 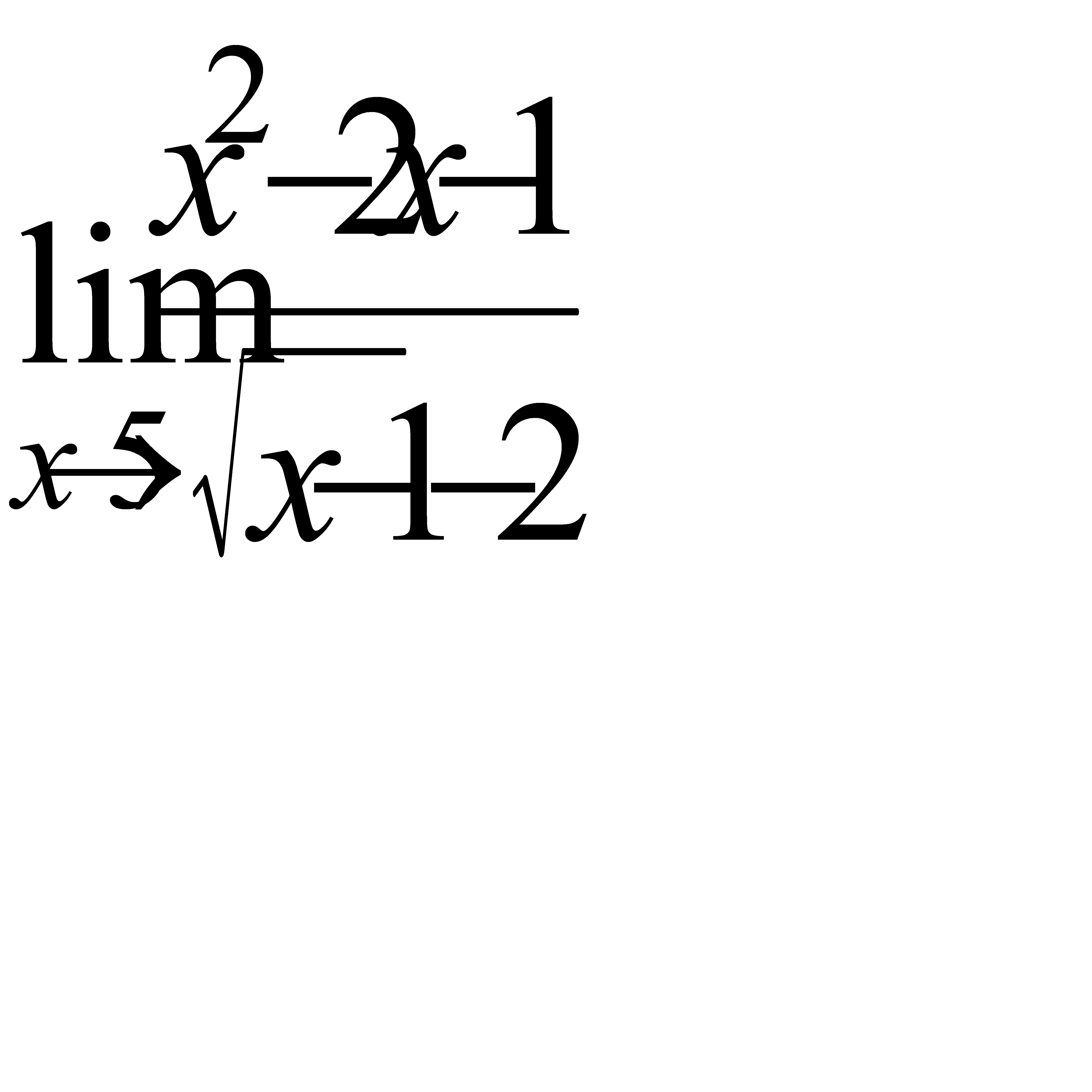 д)
д) 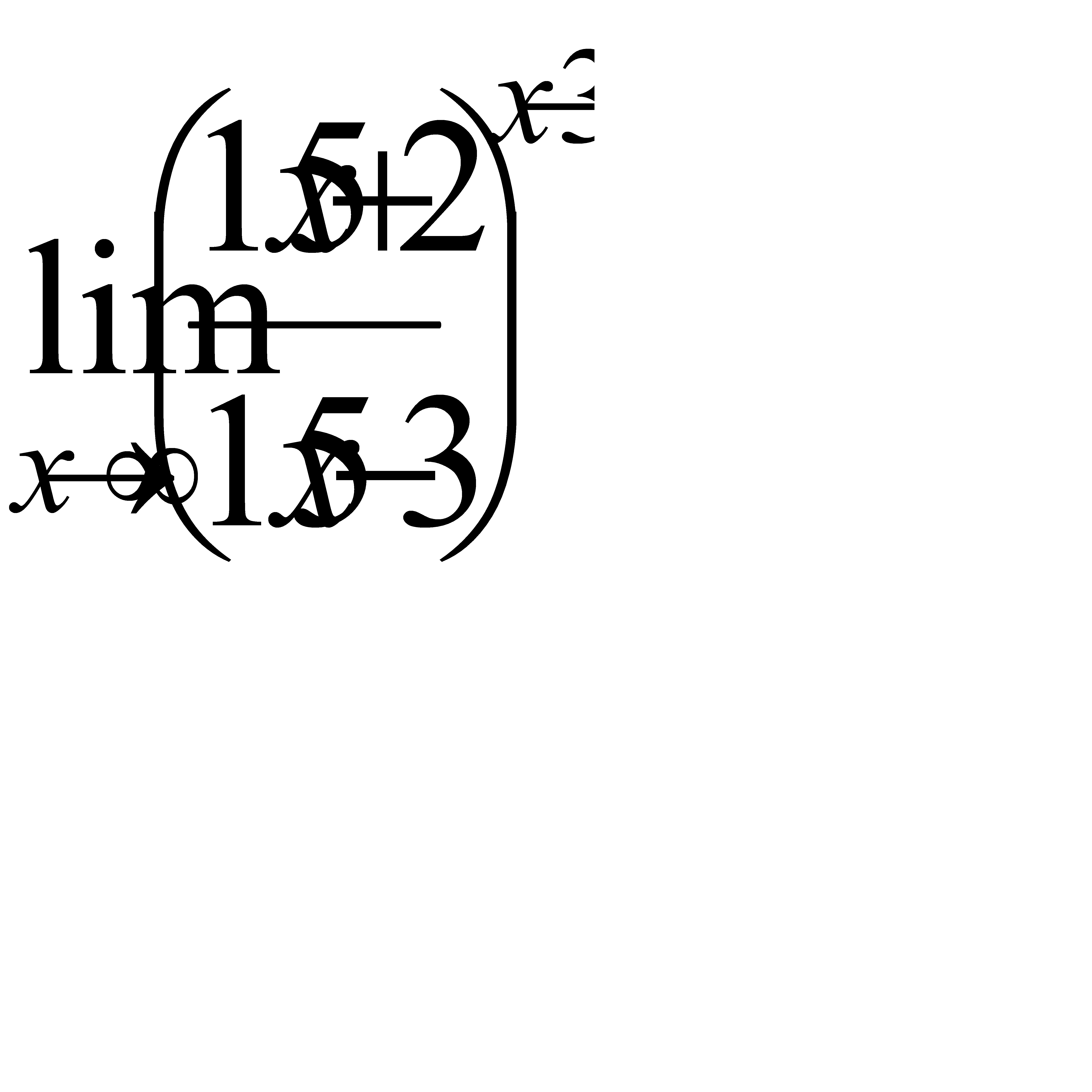
3.3 а) 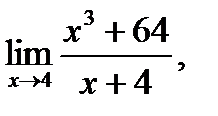 б)
б) 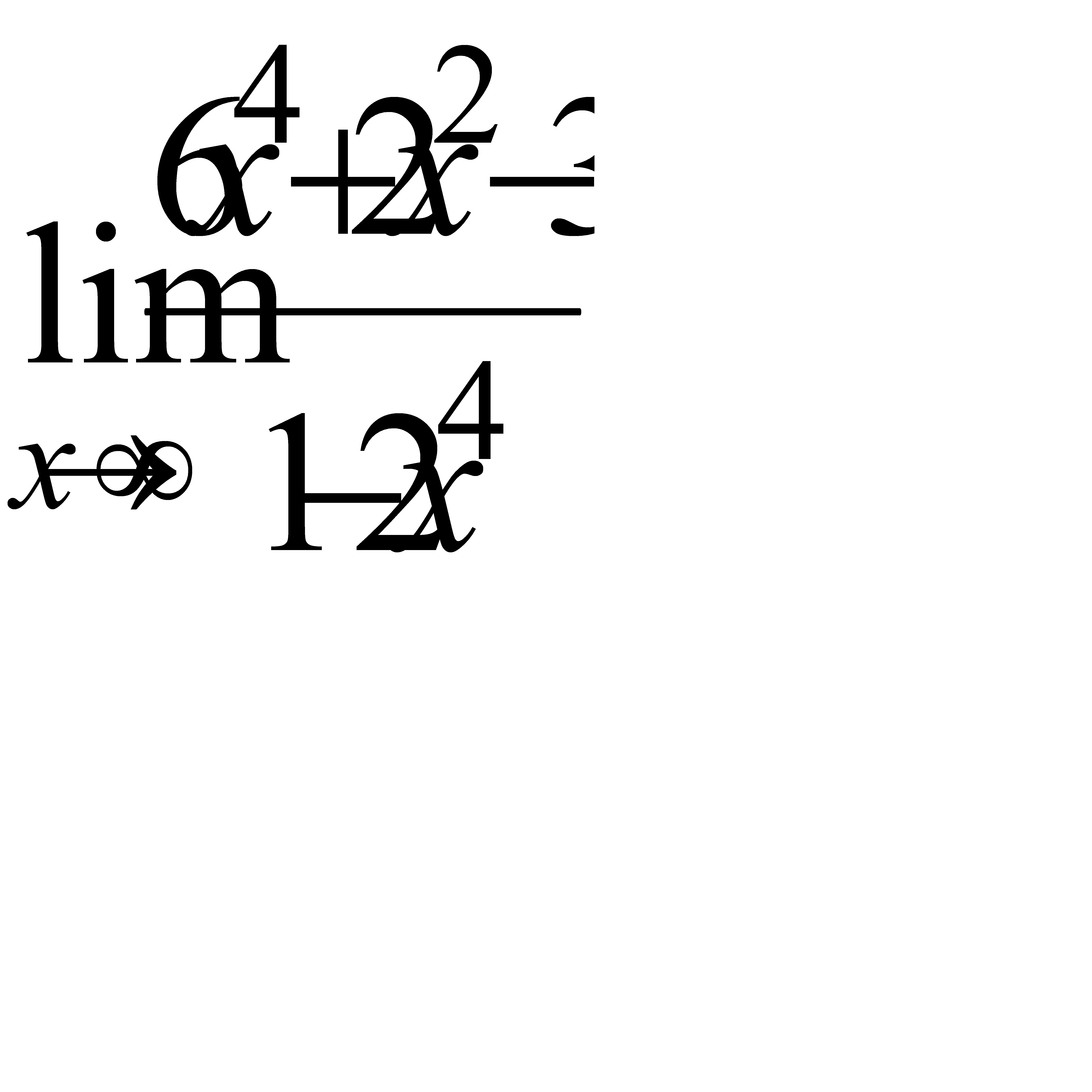 , в)
, в) 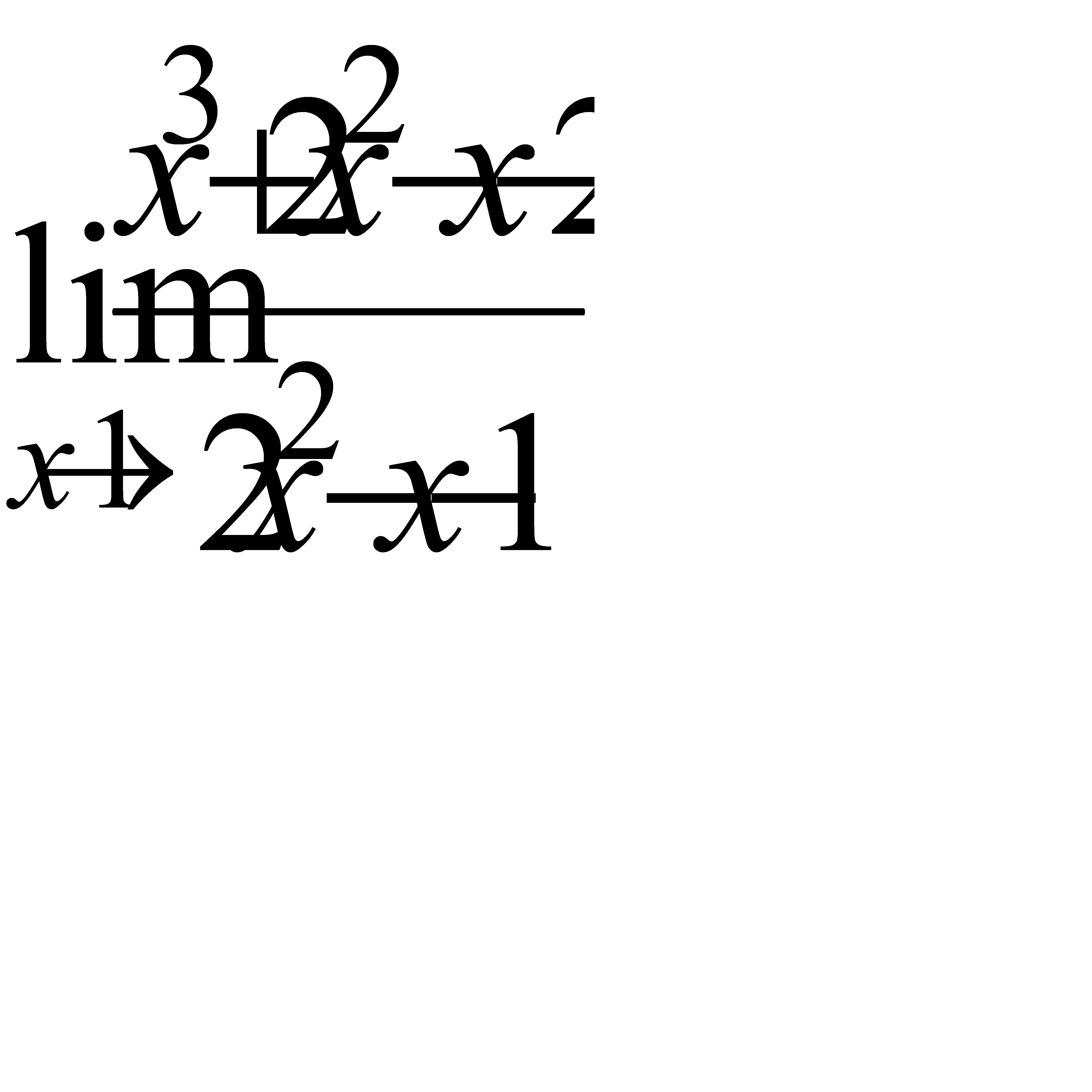 ,
,
г) 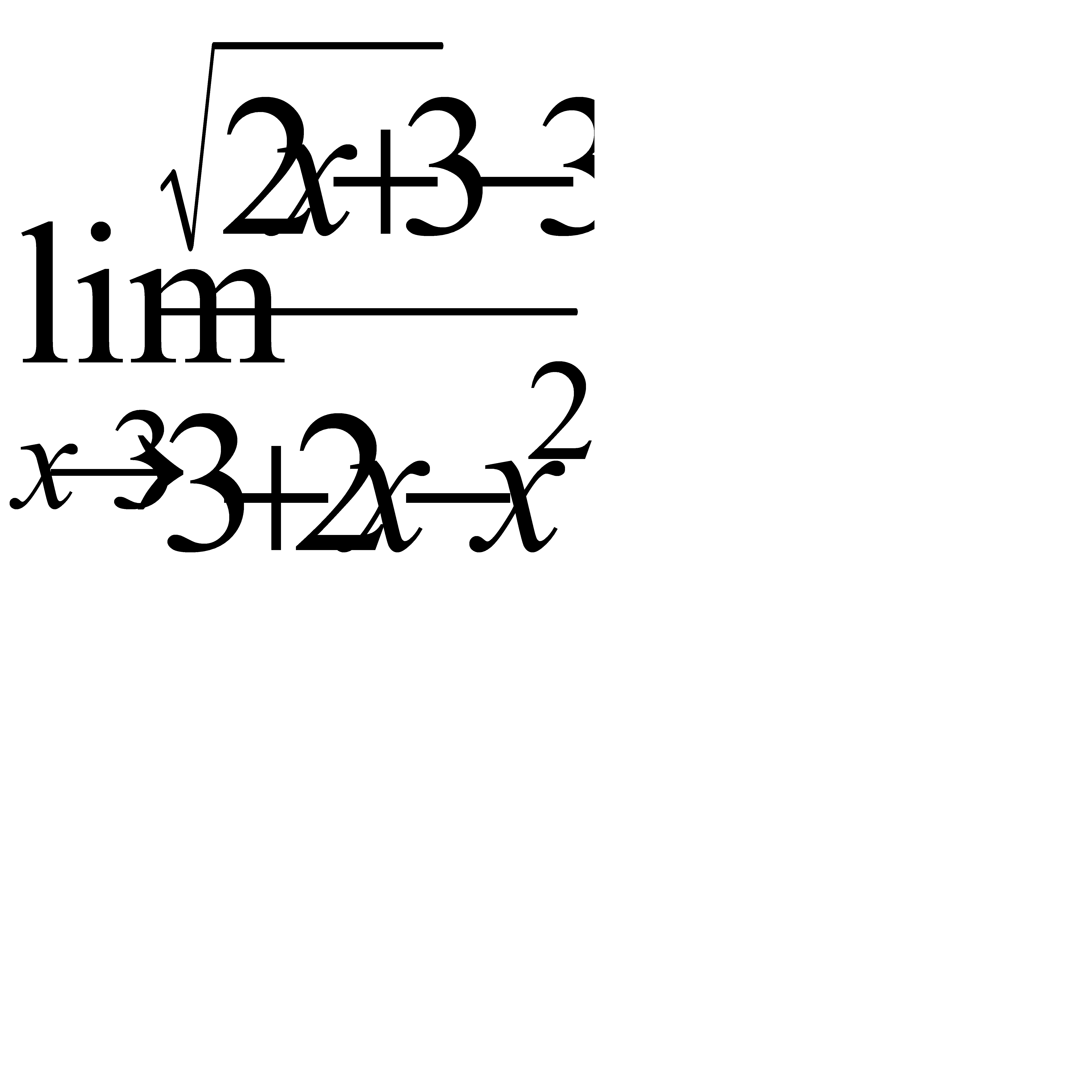 , д)
, д) 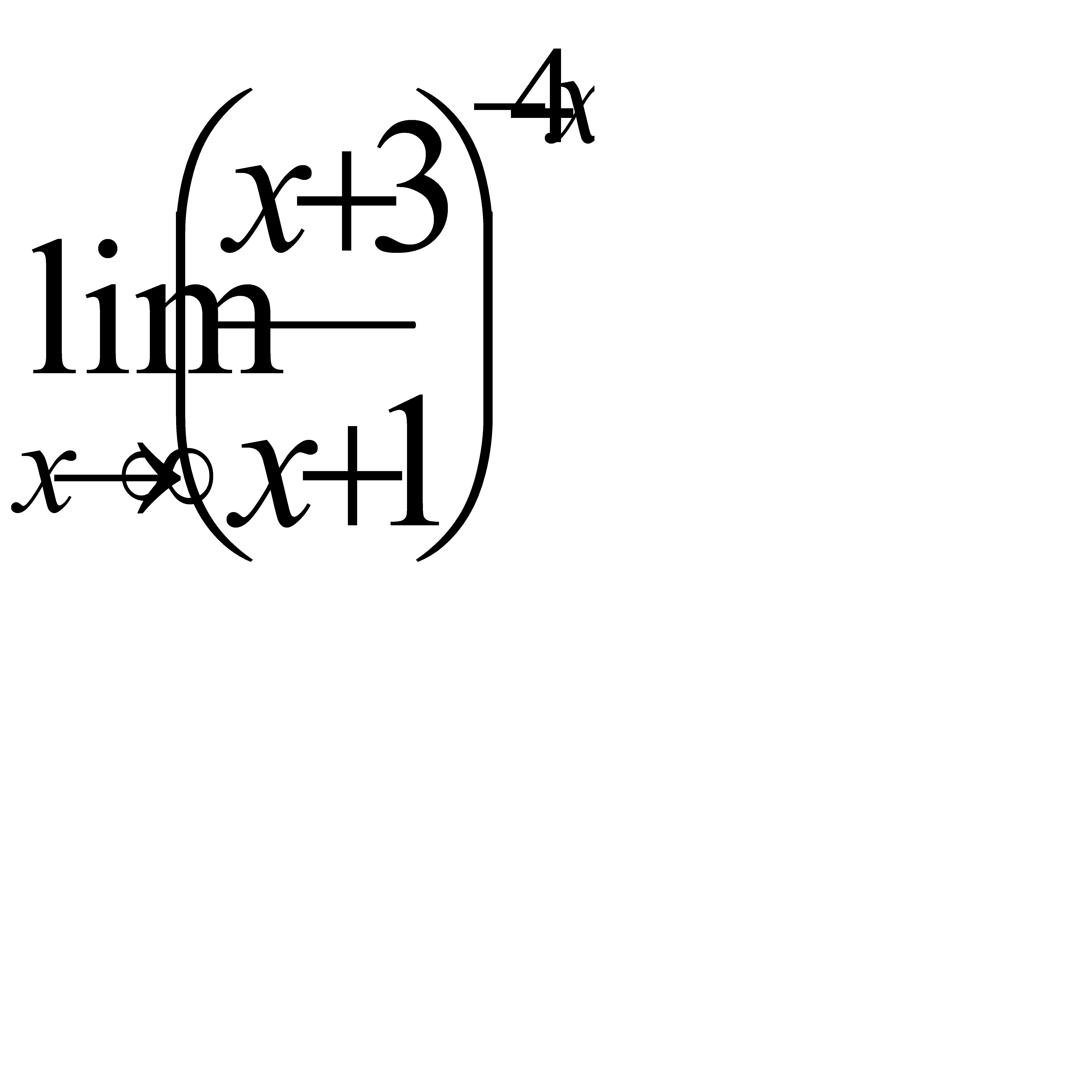
3.4 а)  , б)
, б) 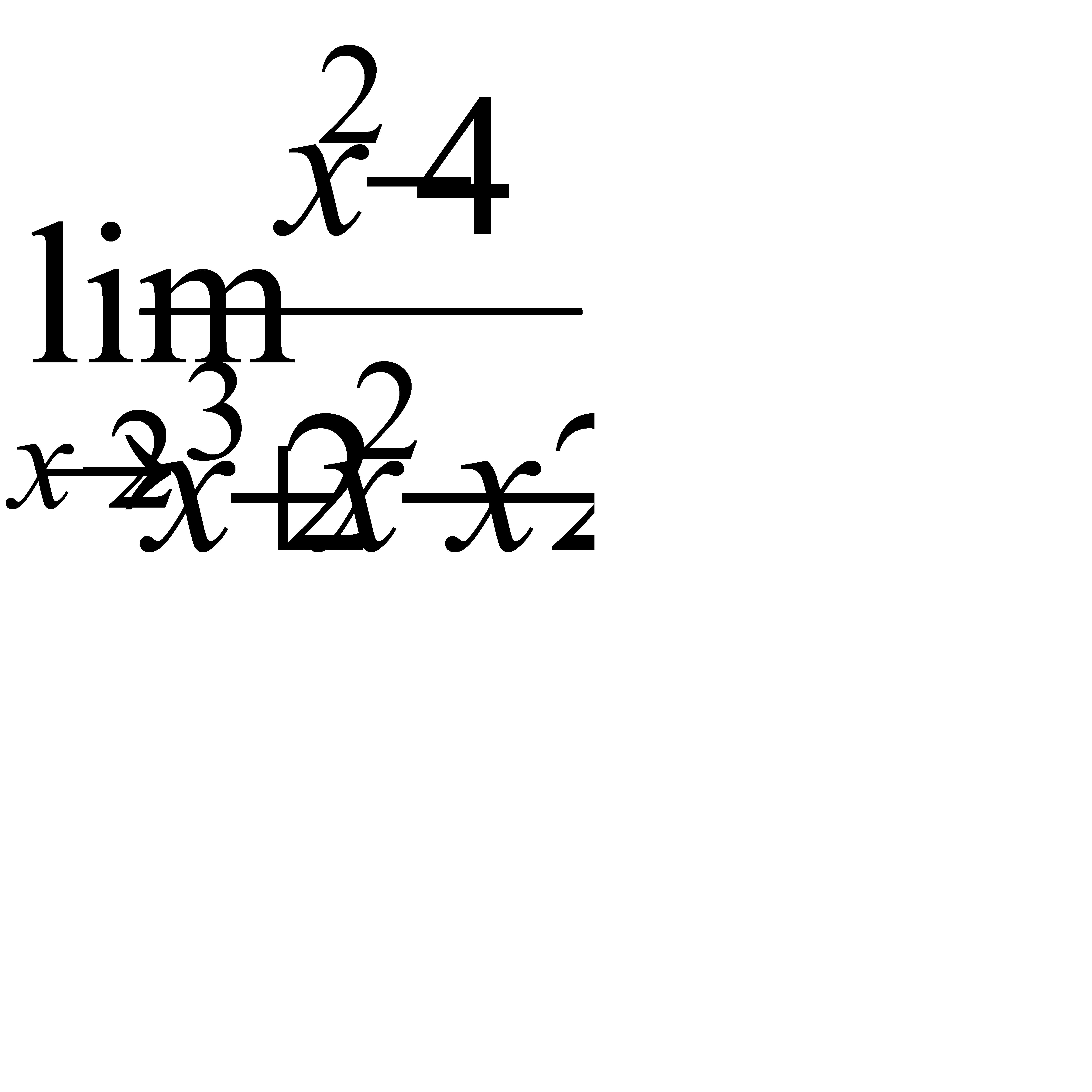 , в)
, в) 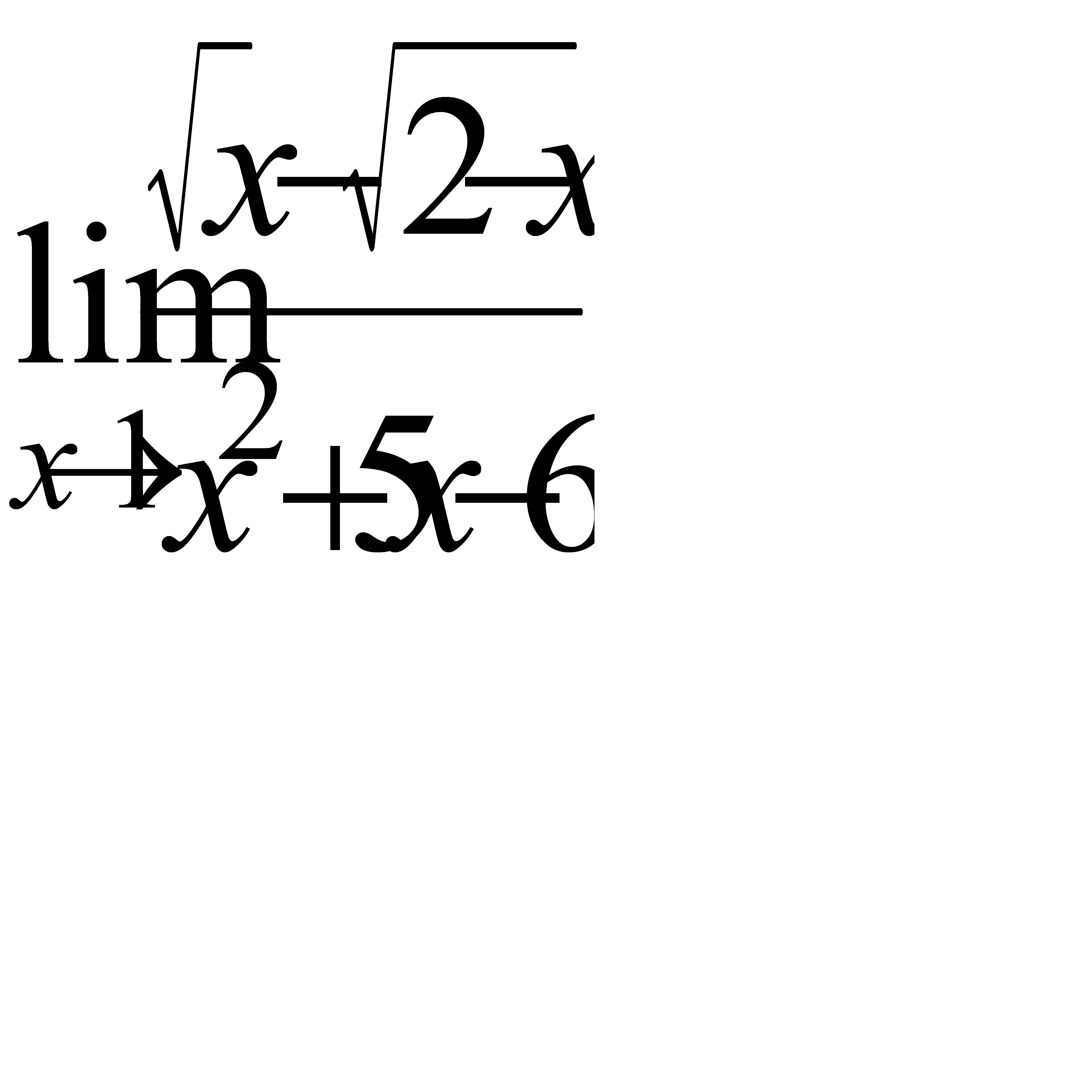 ,
,
г) 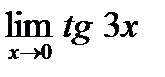 , д)
, д) 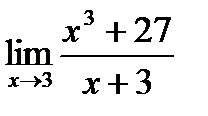
3.5 а) 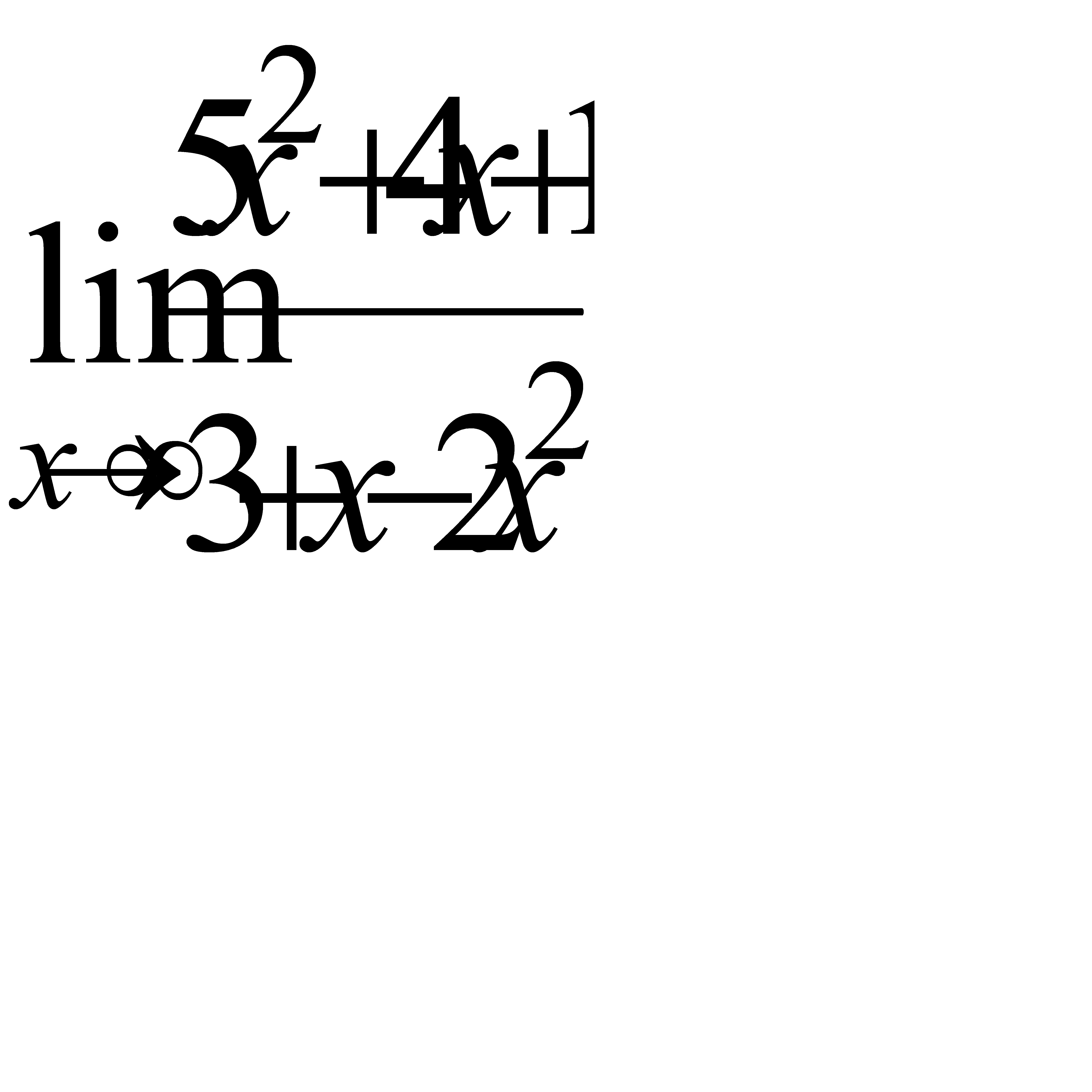 , б)
, б) 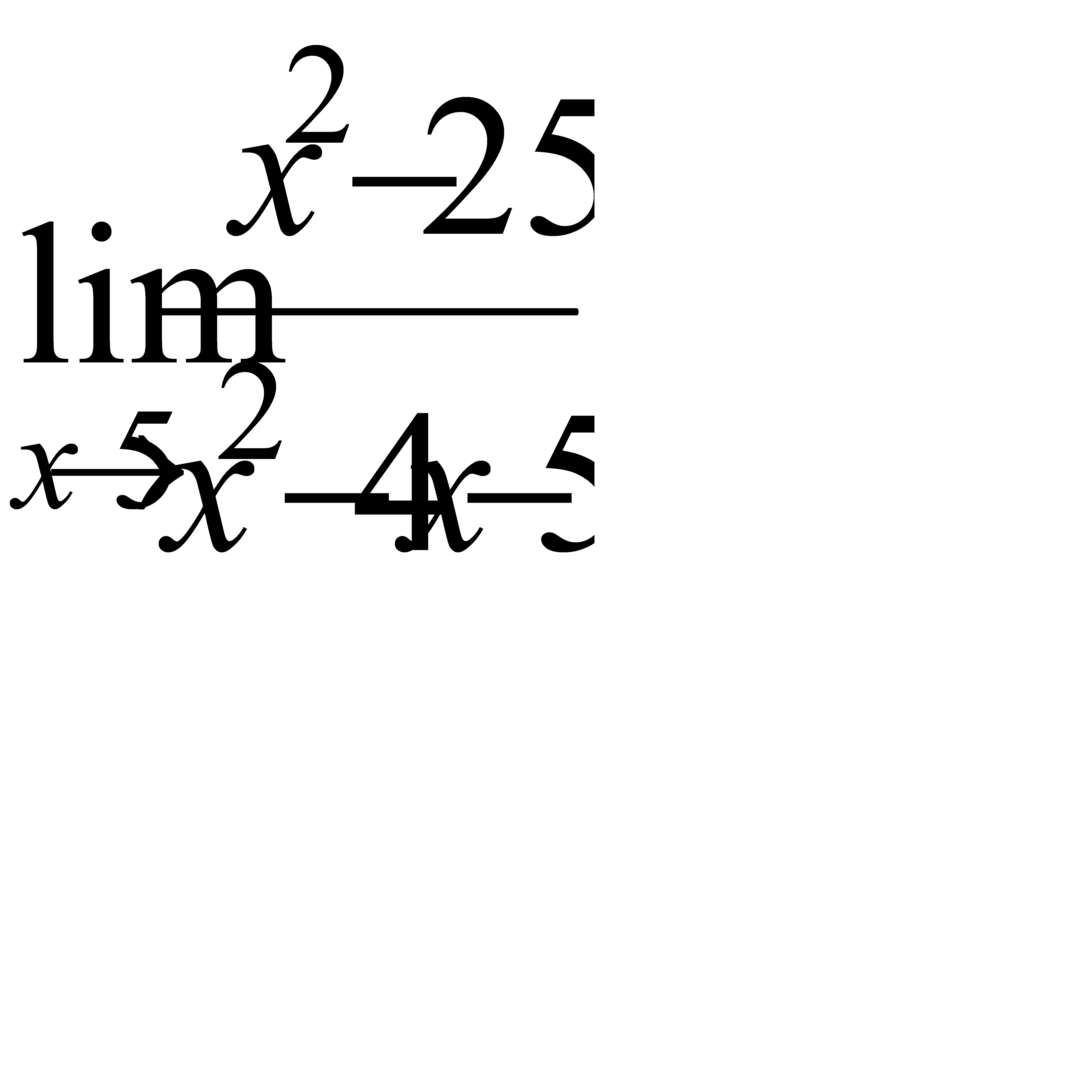 , в)
, в) 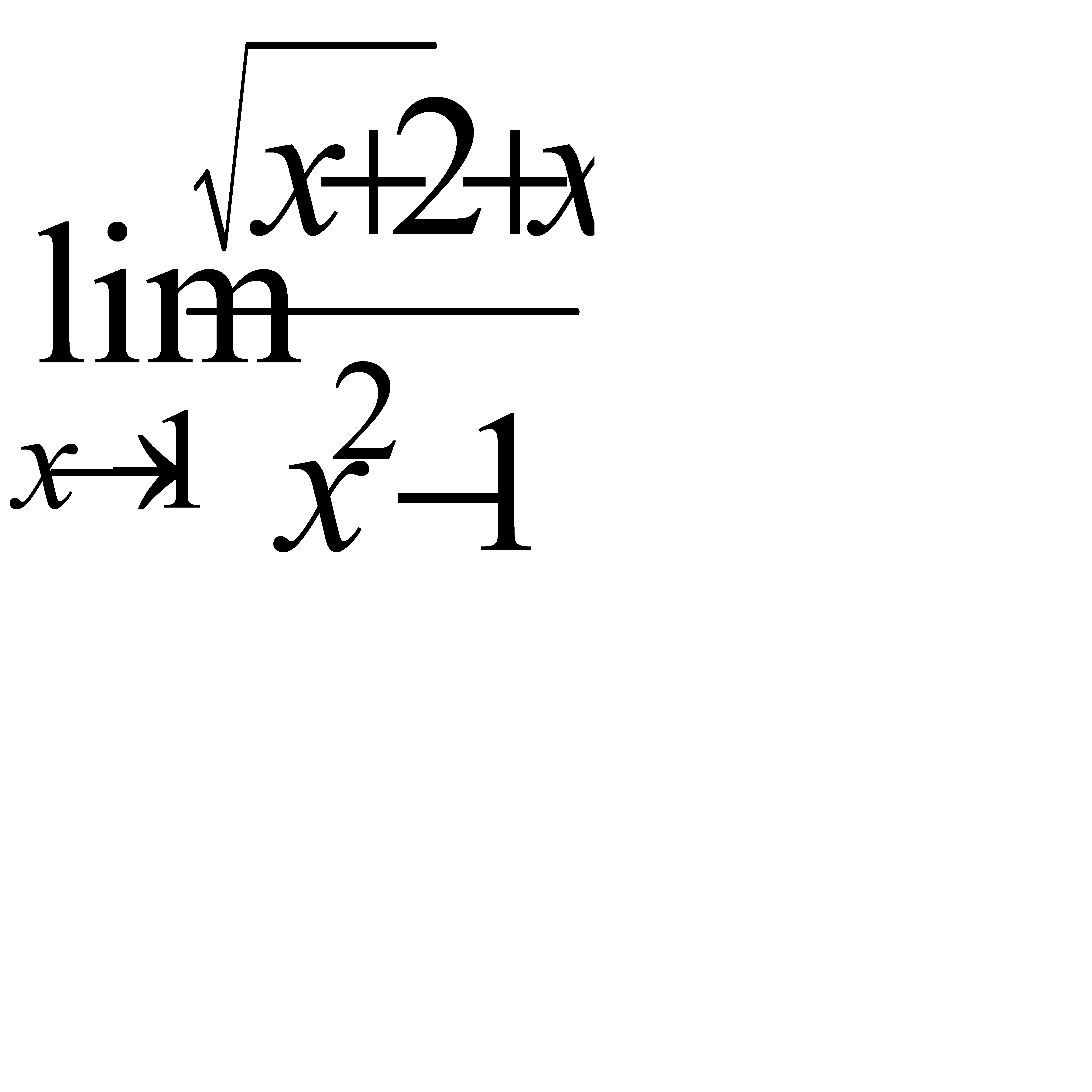 ,
,
г) 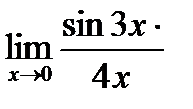 , д)
, д) 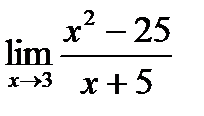
3.6 а)  , б)
, б) 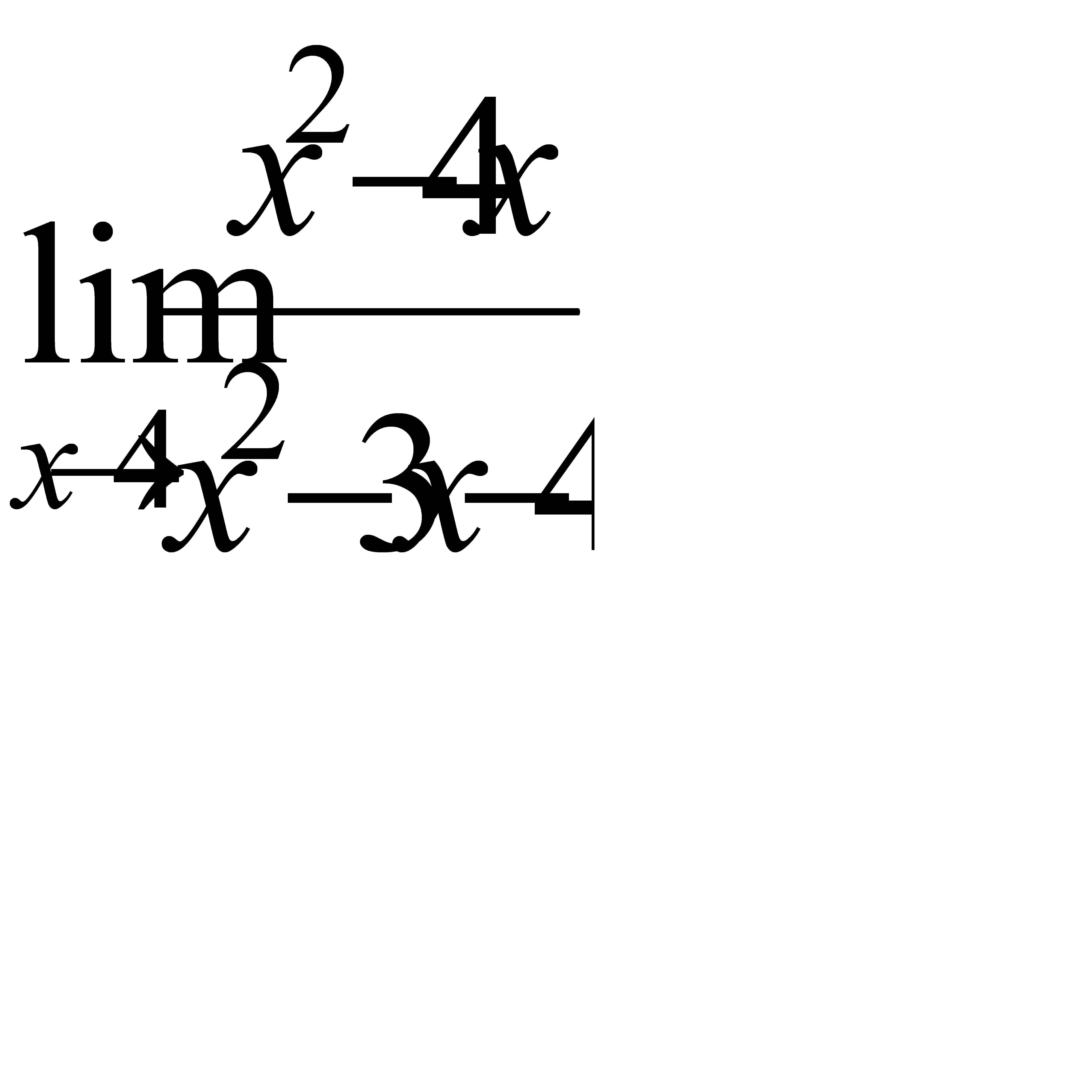 , в)
, в) 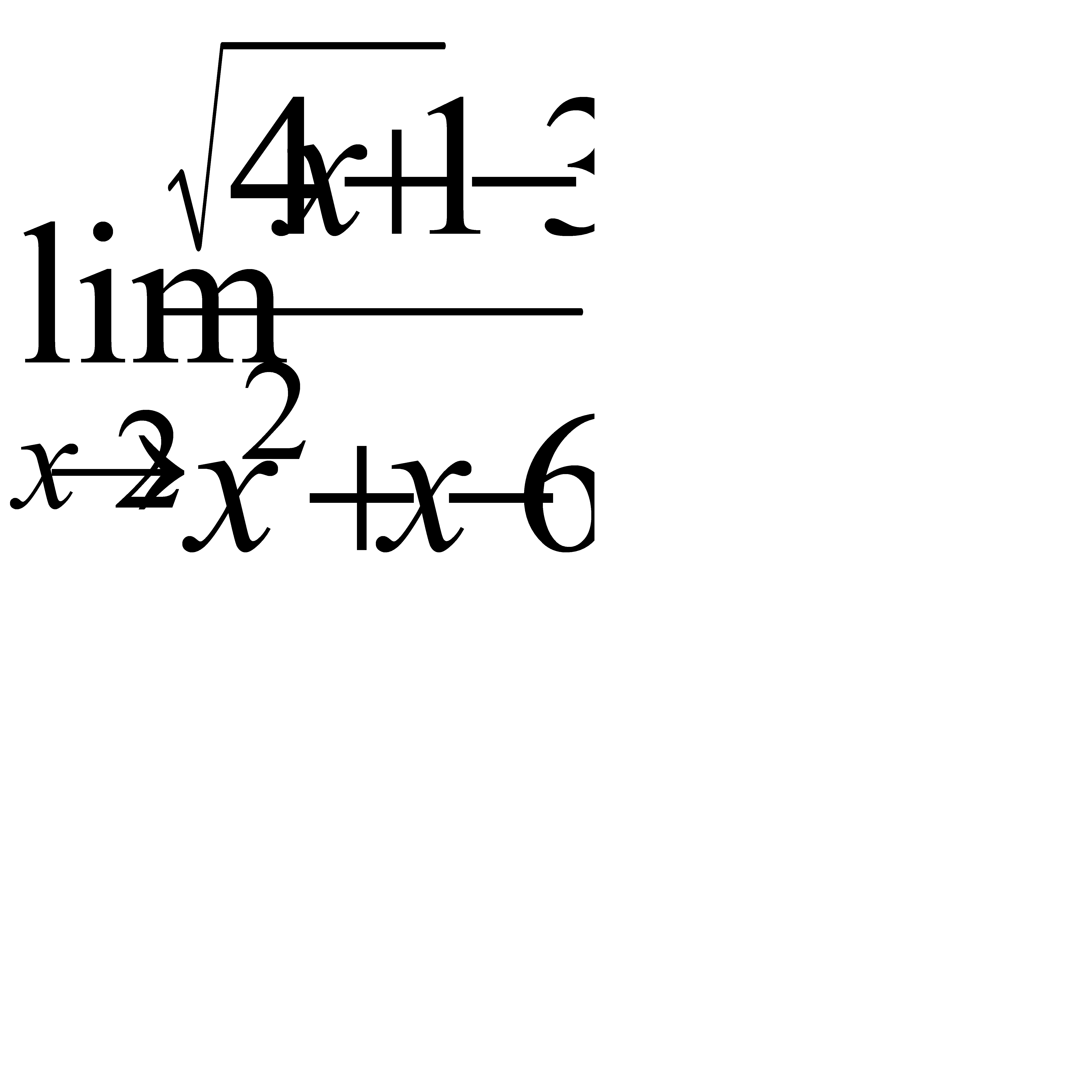 ,
,
г) 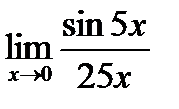 , д)
, д) 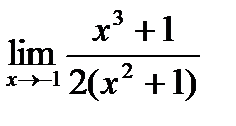
3.7 а) 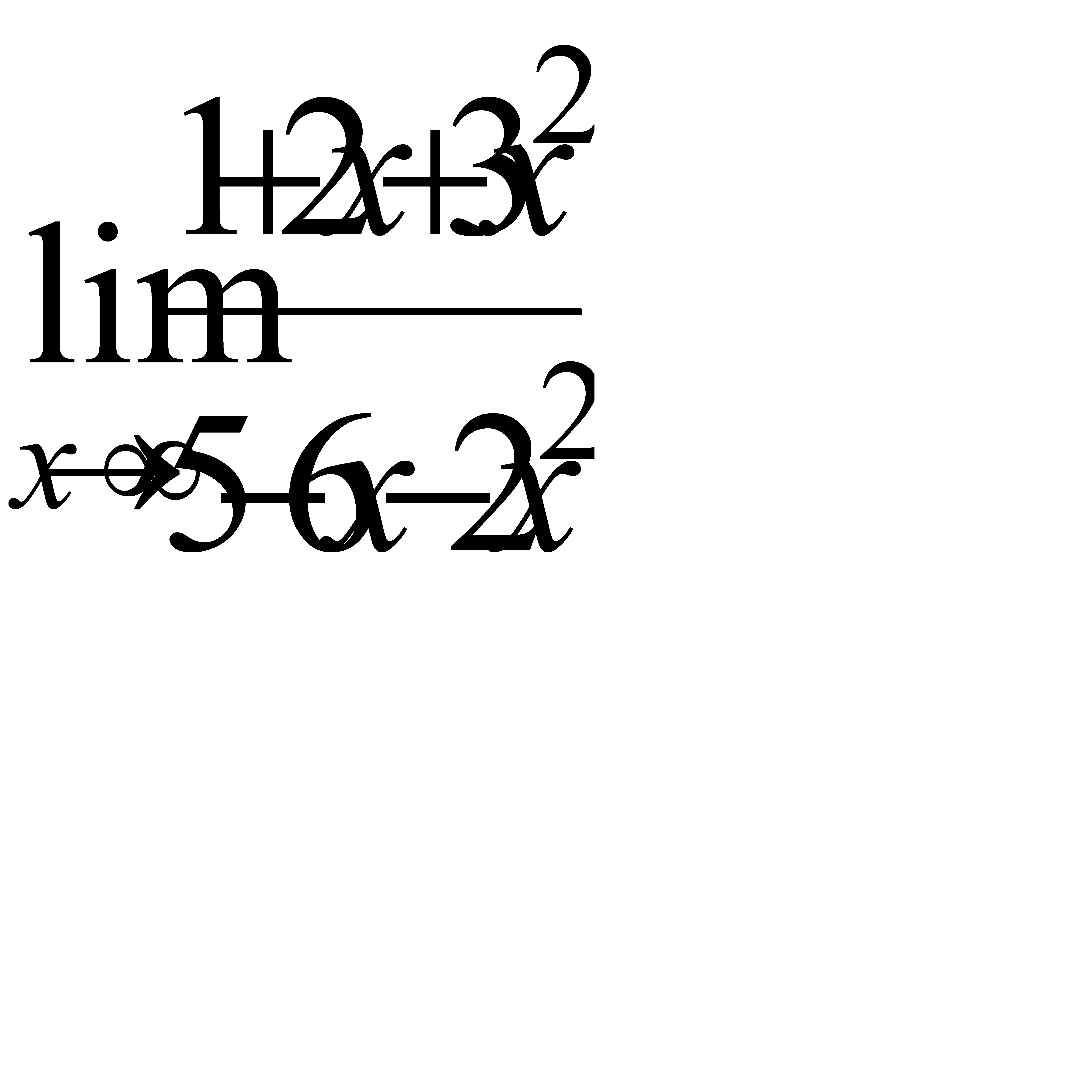 , б)
, б) 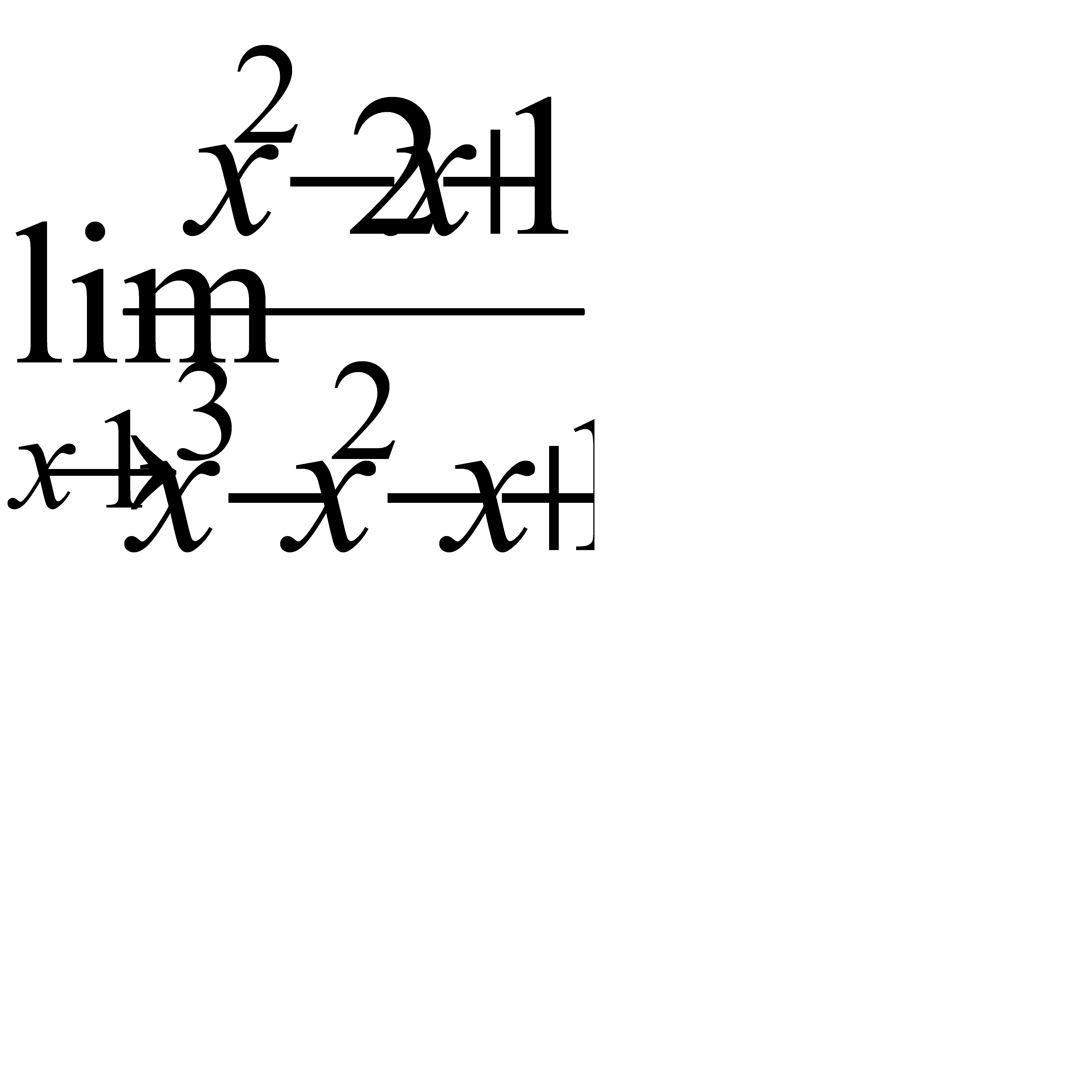 , в)
, в) 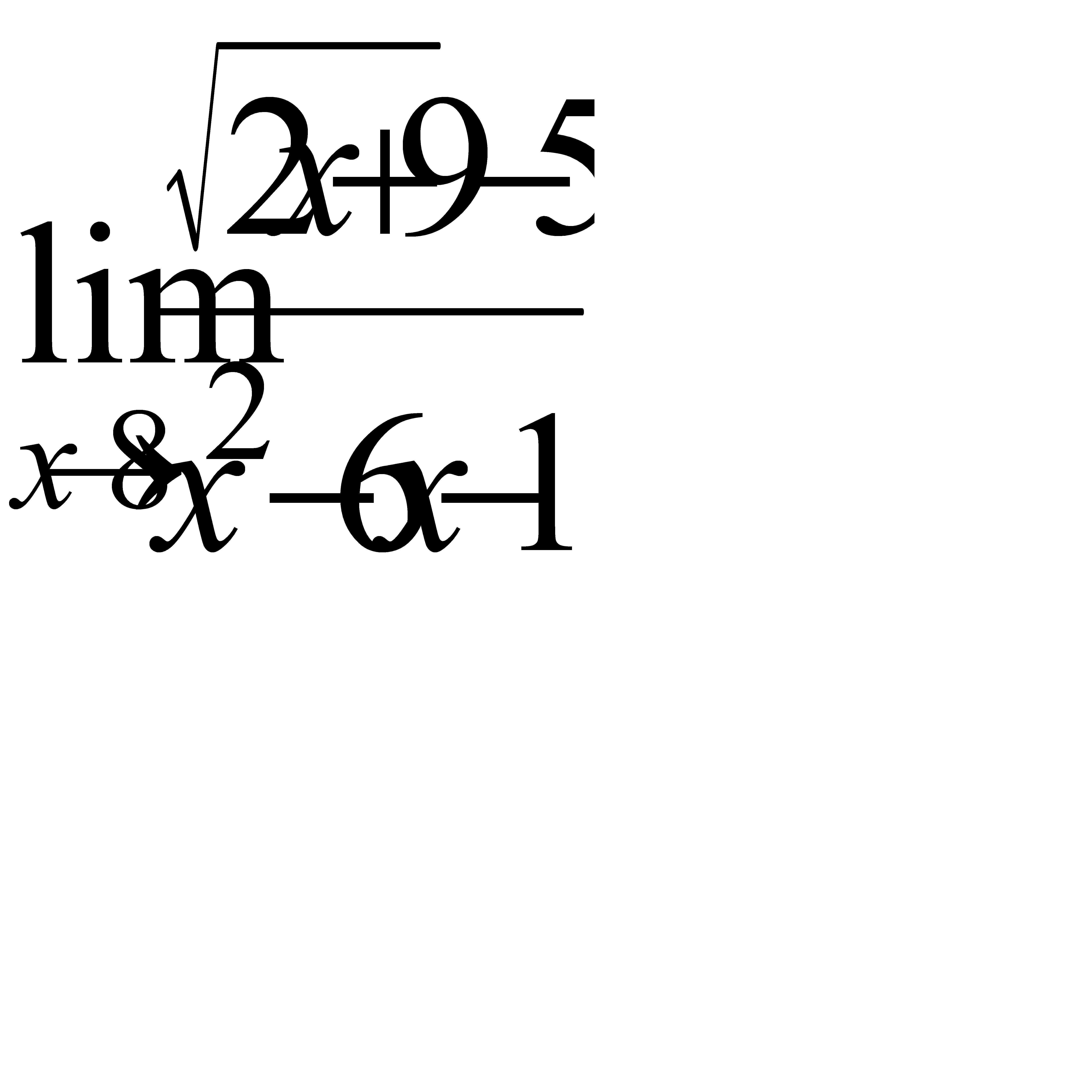 ,
,
г) 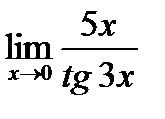 , д)
, д) 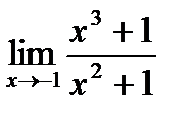
3.8 а)  , б)
, б) 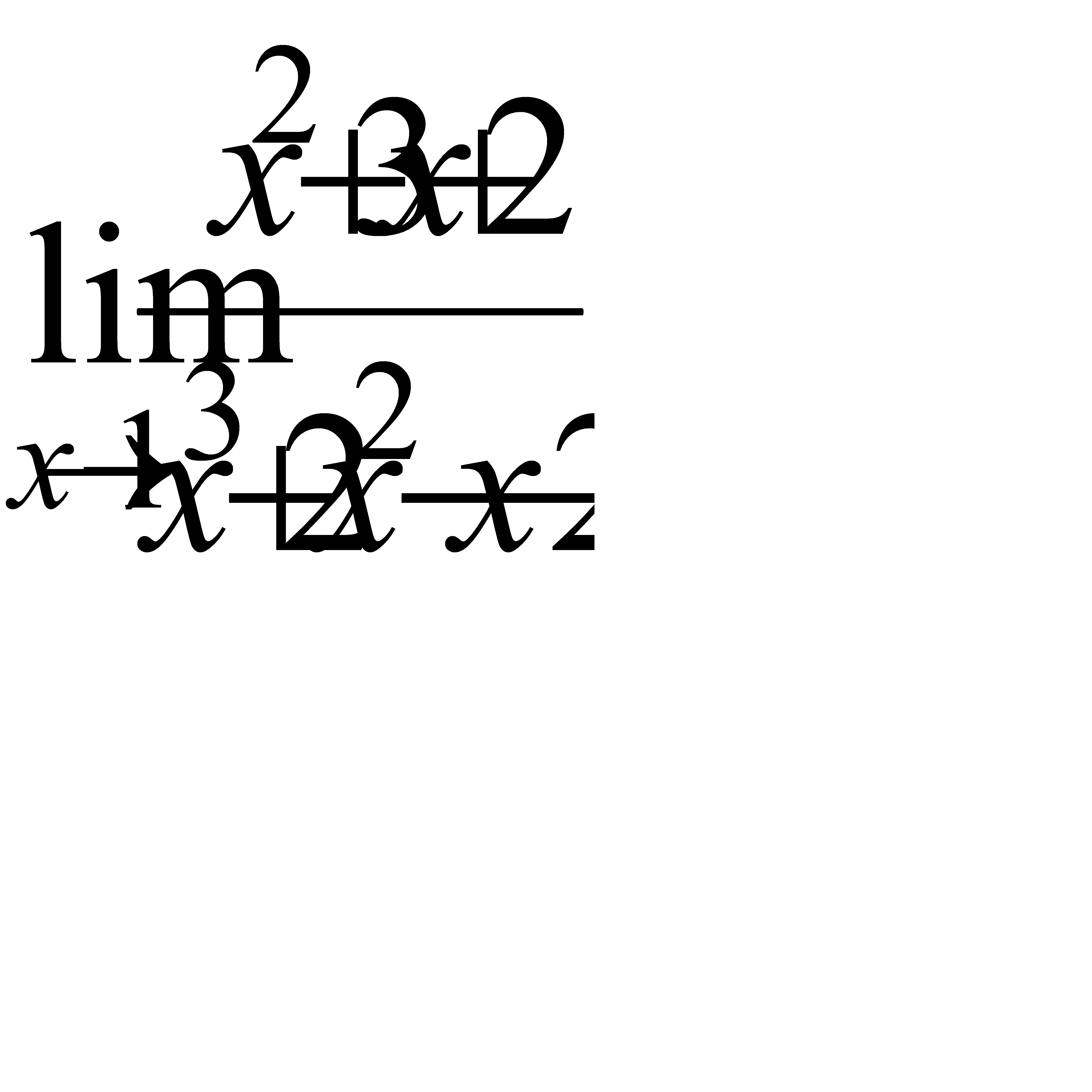 , в)
, в) 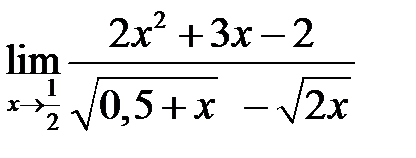 ,
,
г) 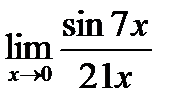 , д)
, д) 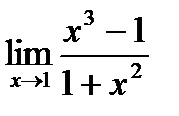
3.9 а)  , б)
, б) 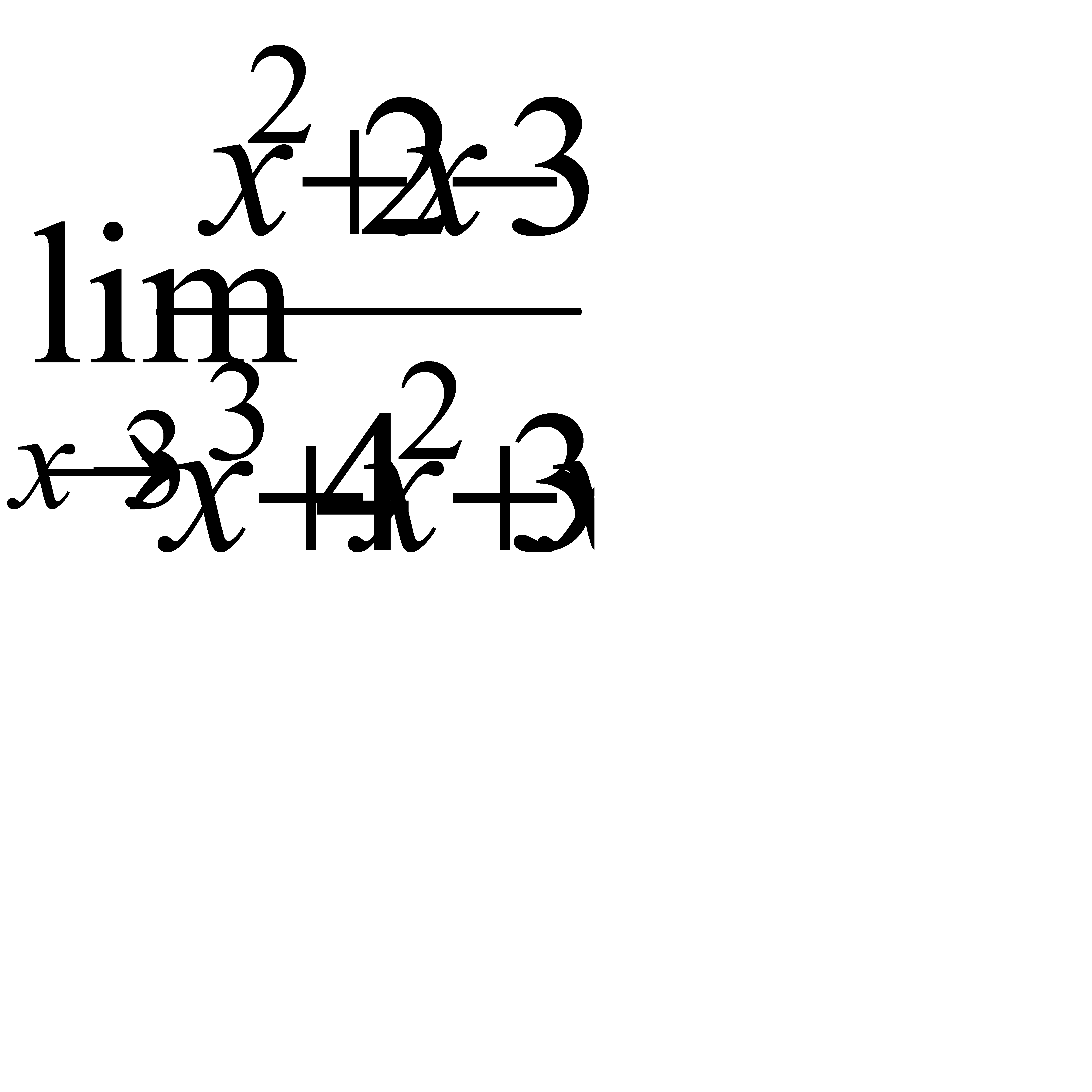 , в)
, в) 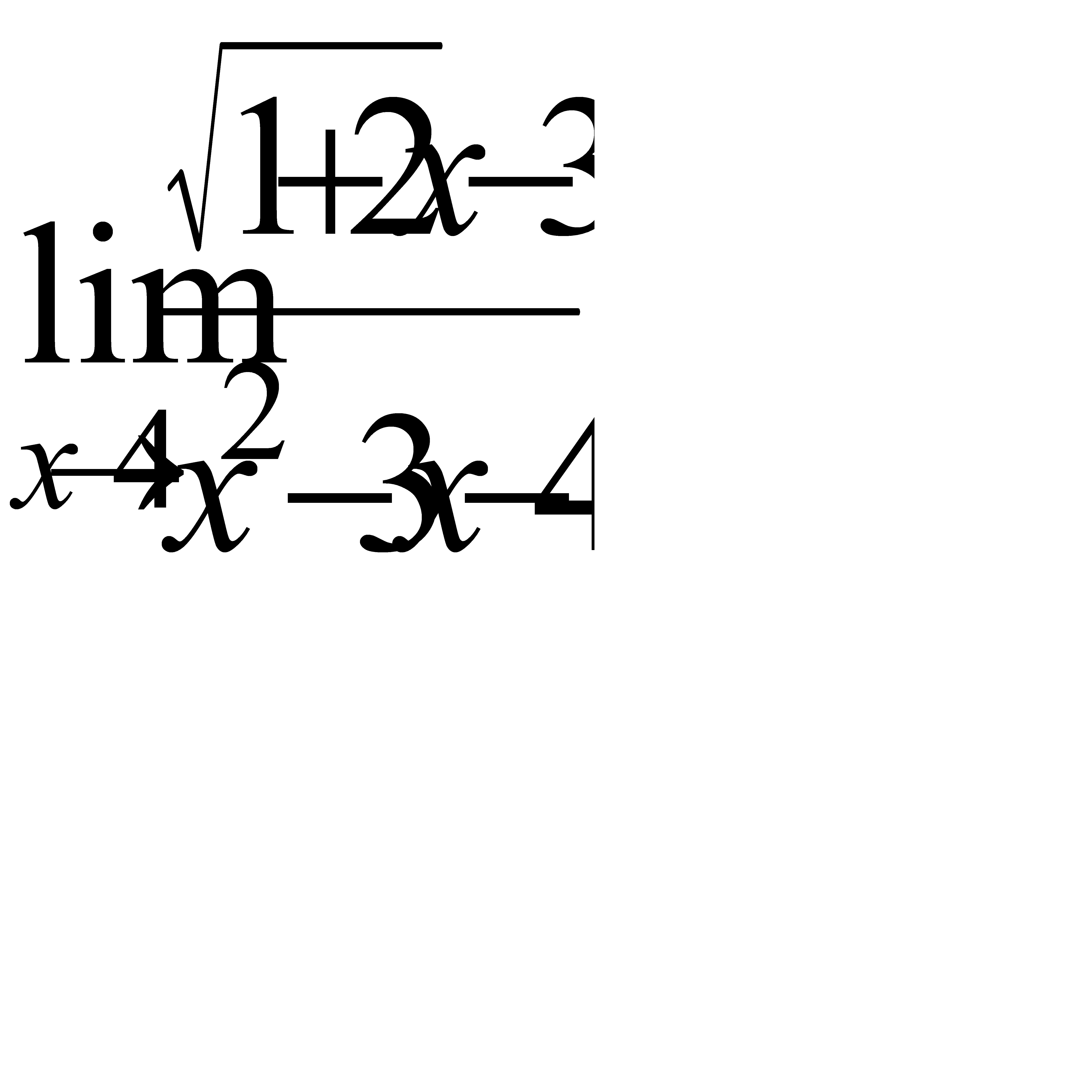 ,
,
г) 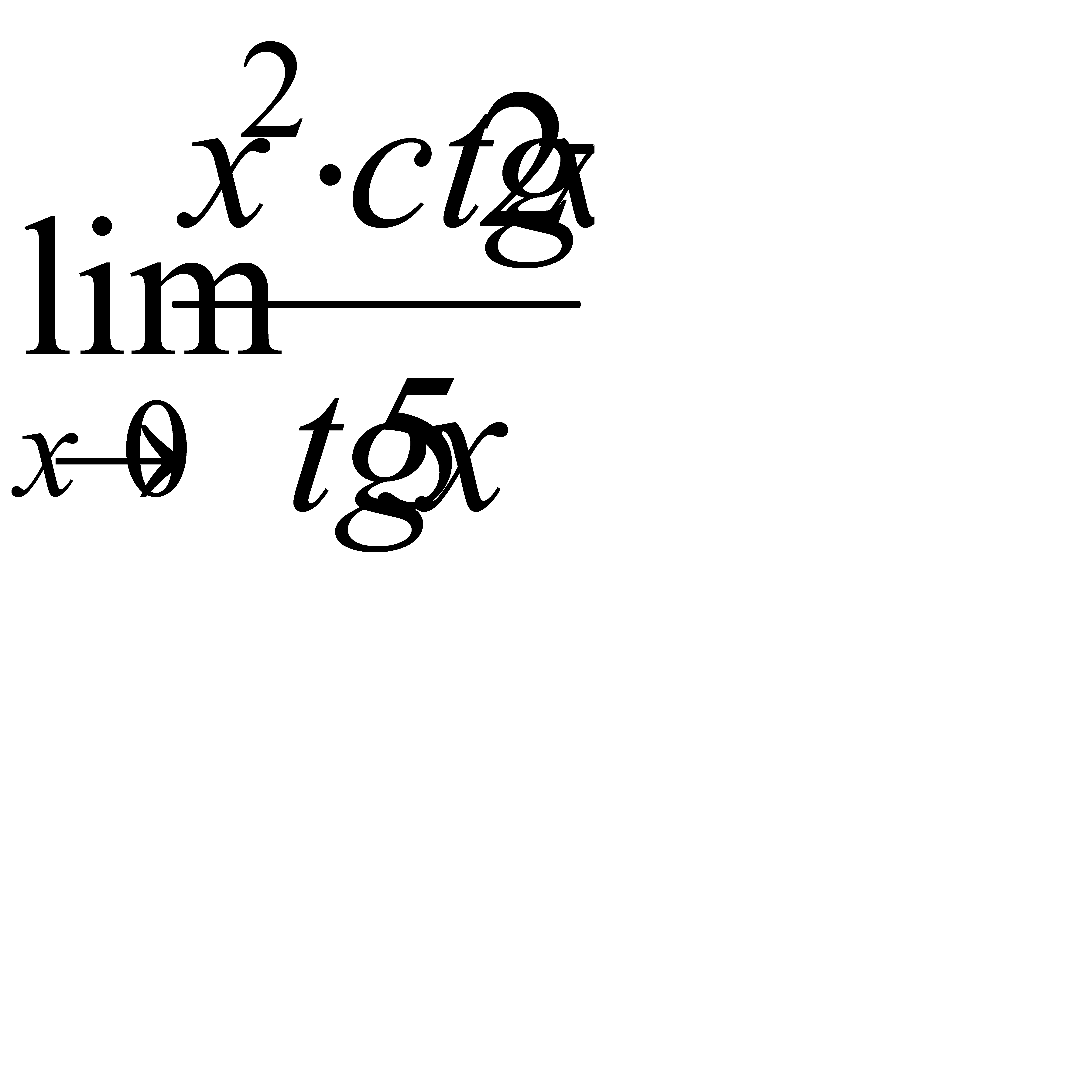 , д)
, д) 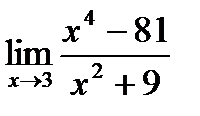
3.10 а) 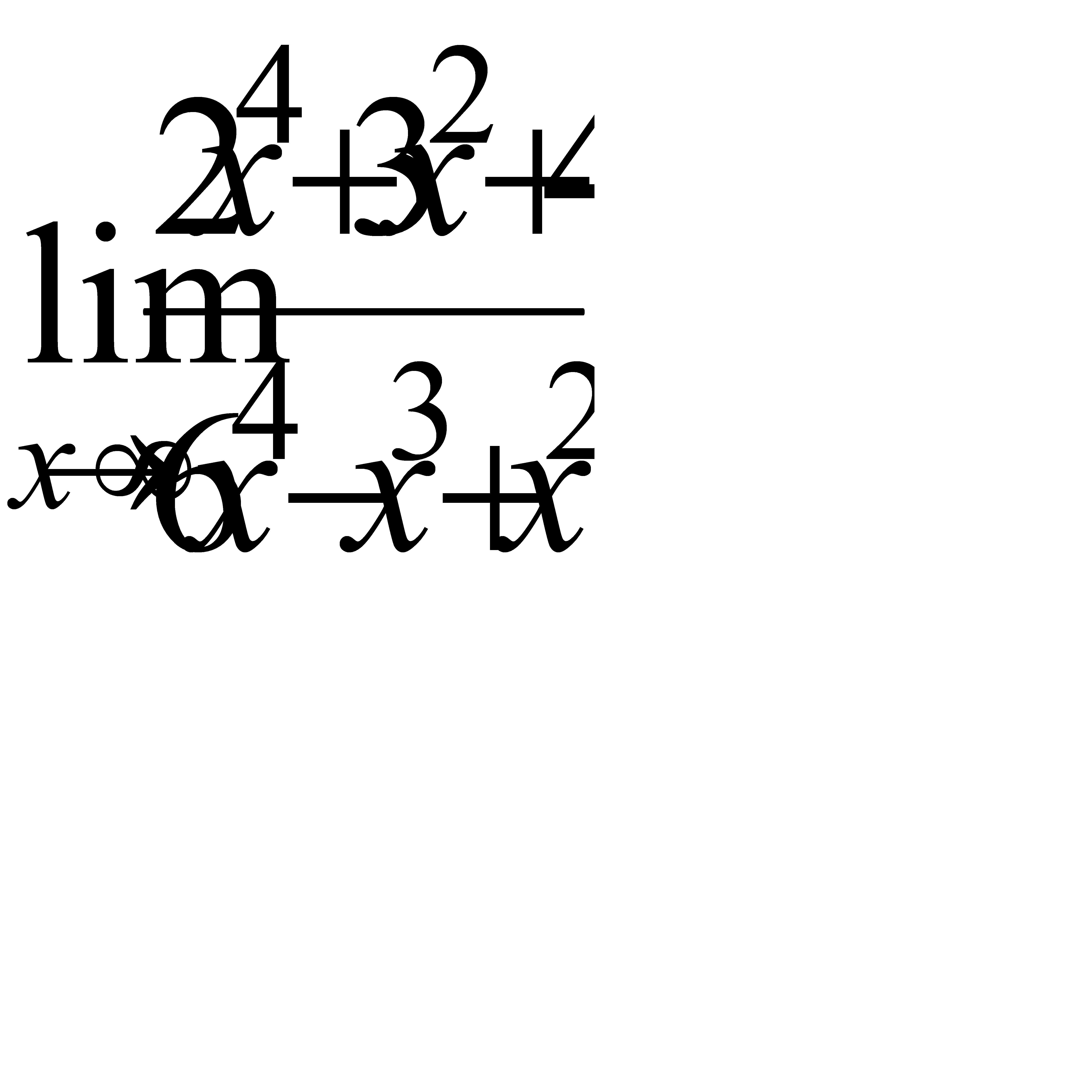 , б)
, б)  , в)
, в) 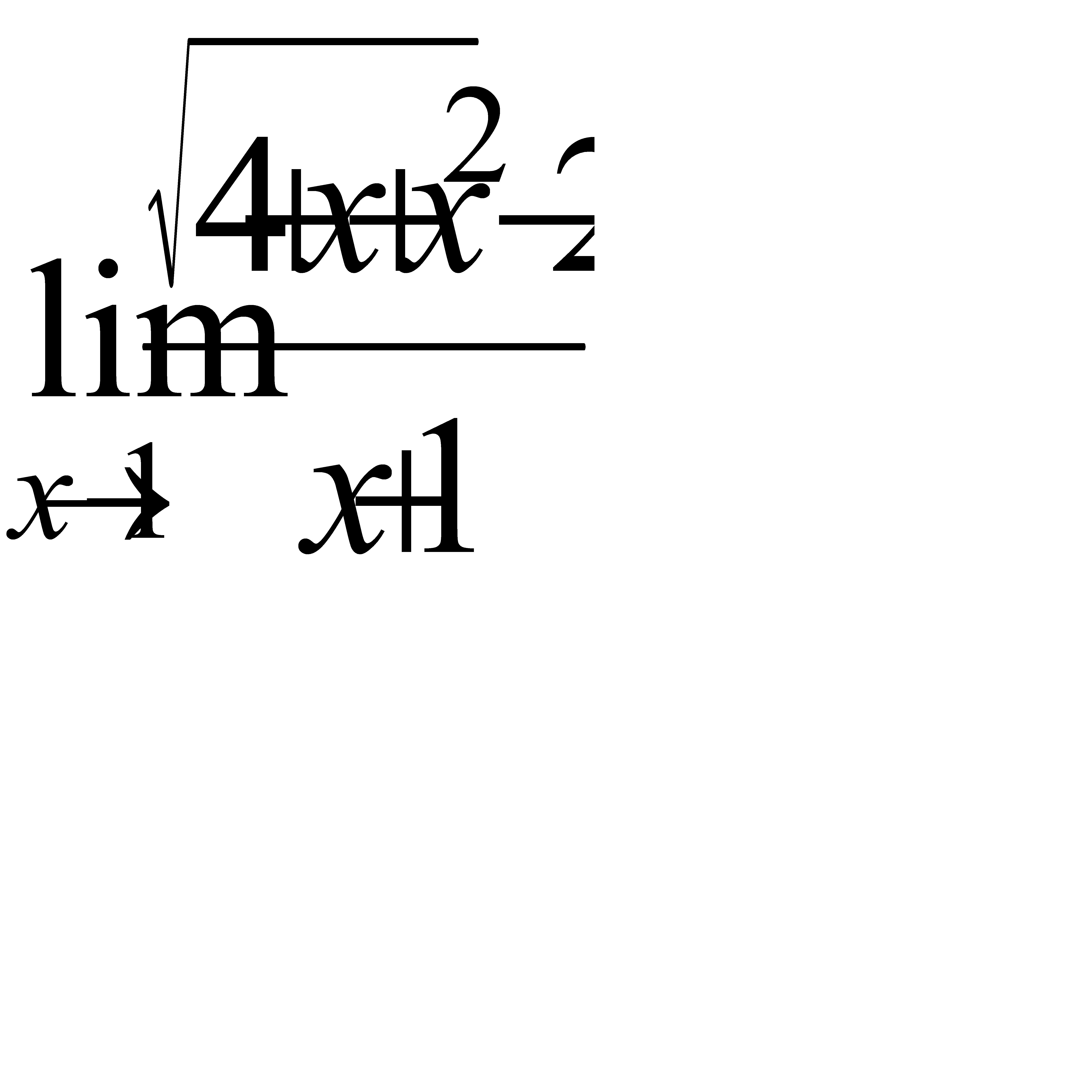 ,
,
г) 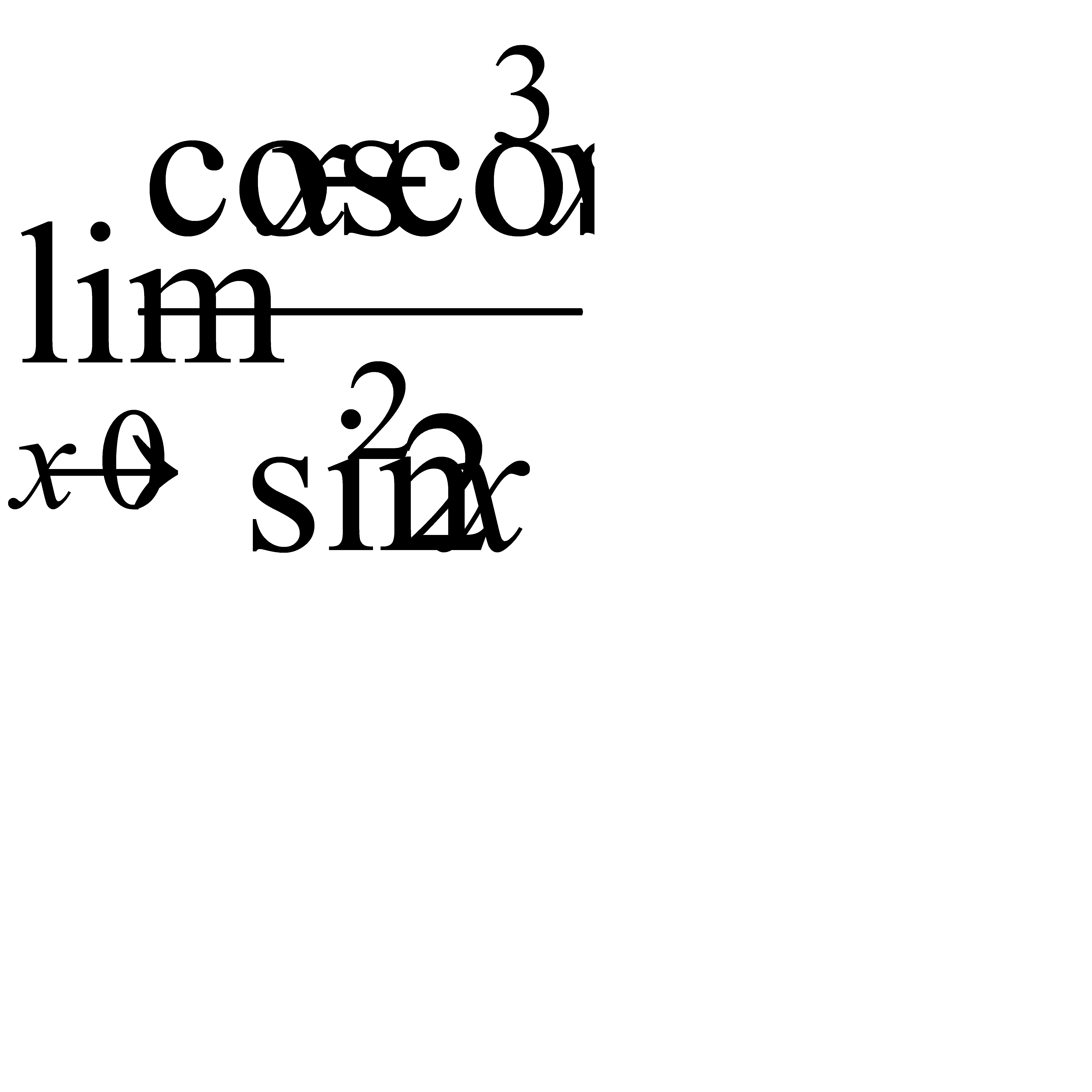 , д)
, д) 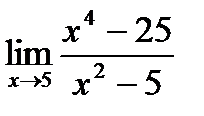
ЗАДАНИЕ4
Найти производные 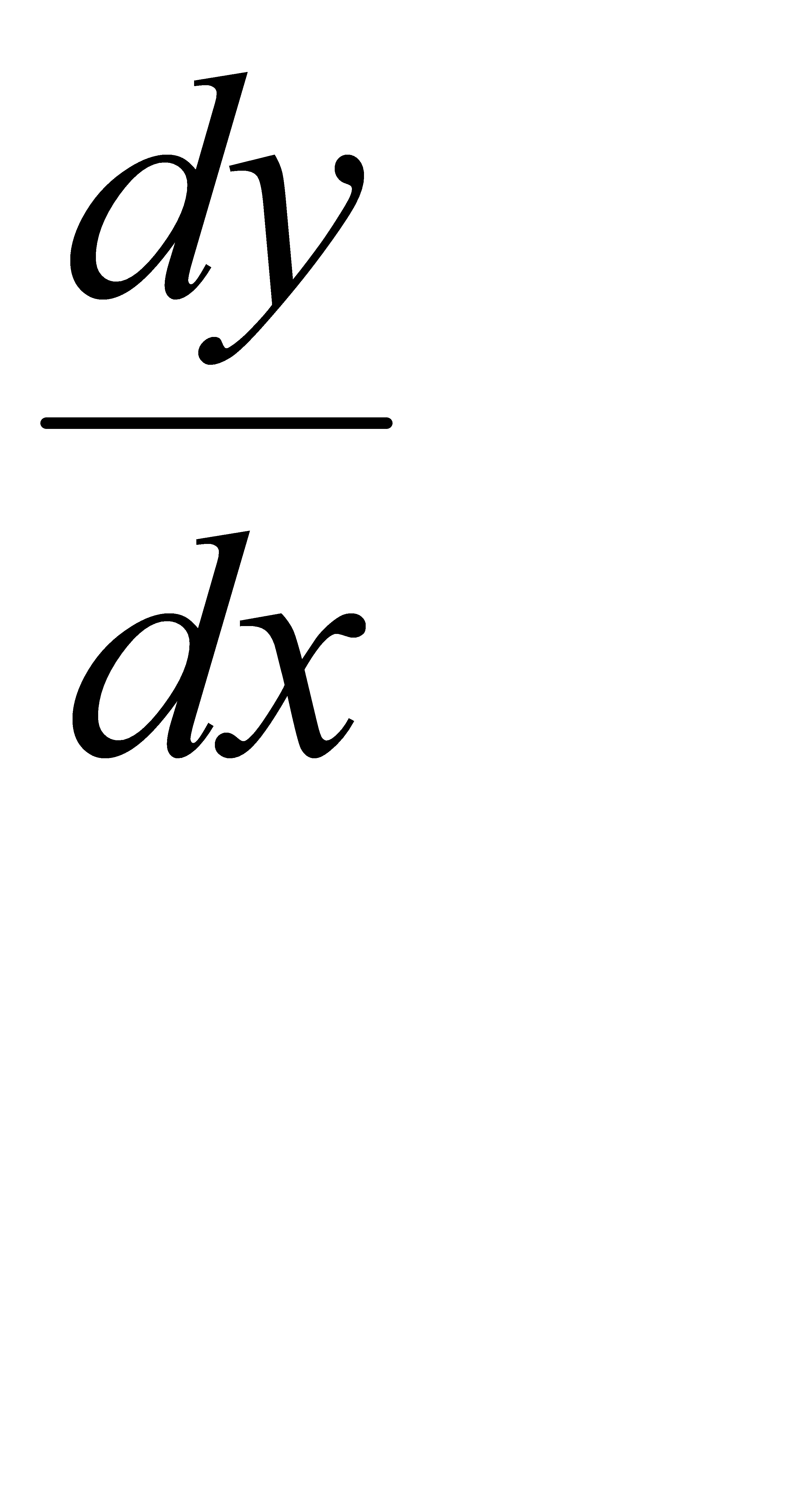 данных функций.
данных функций.
4.1 а) 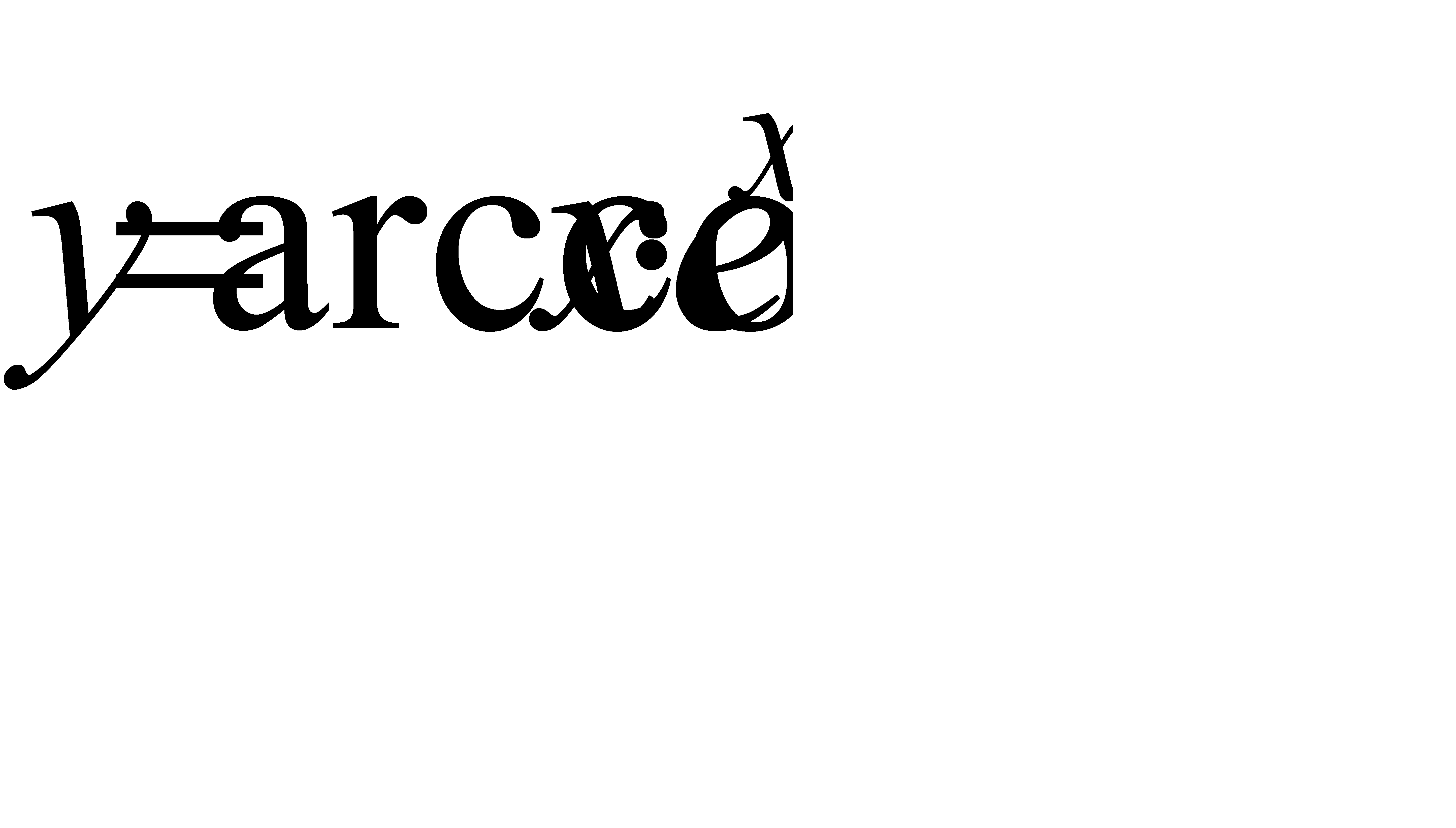 ; б)
; б) 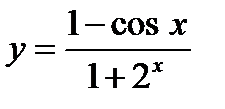 ; в)
; в) 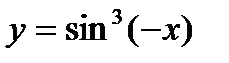 .
.
4.2 а) 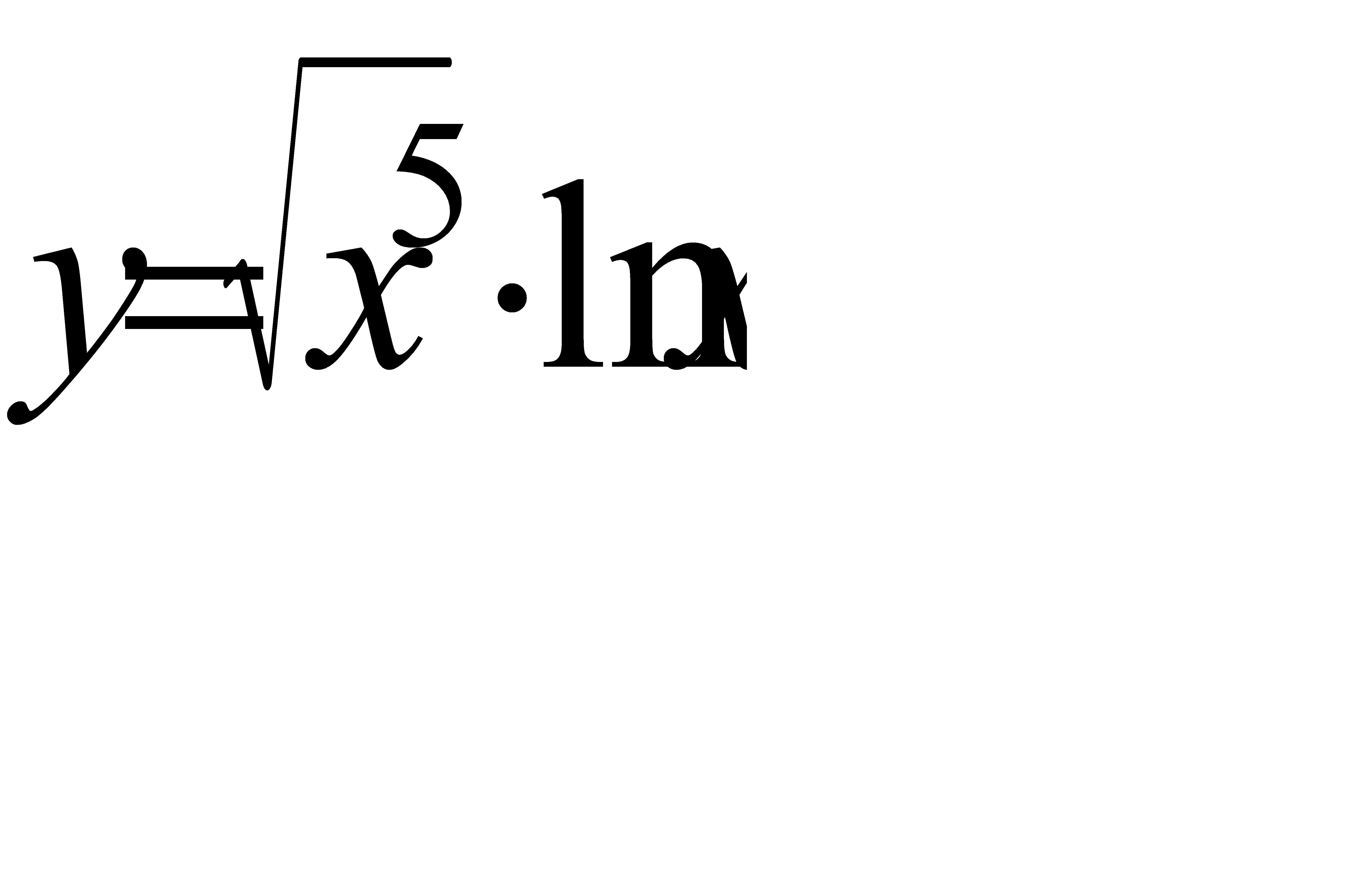 ; б)
; б) 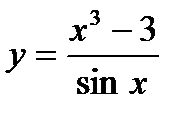 ;в)
;в) 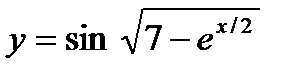 .
.
4.3 а) 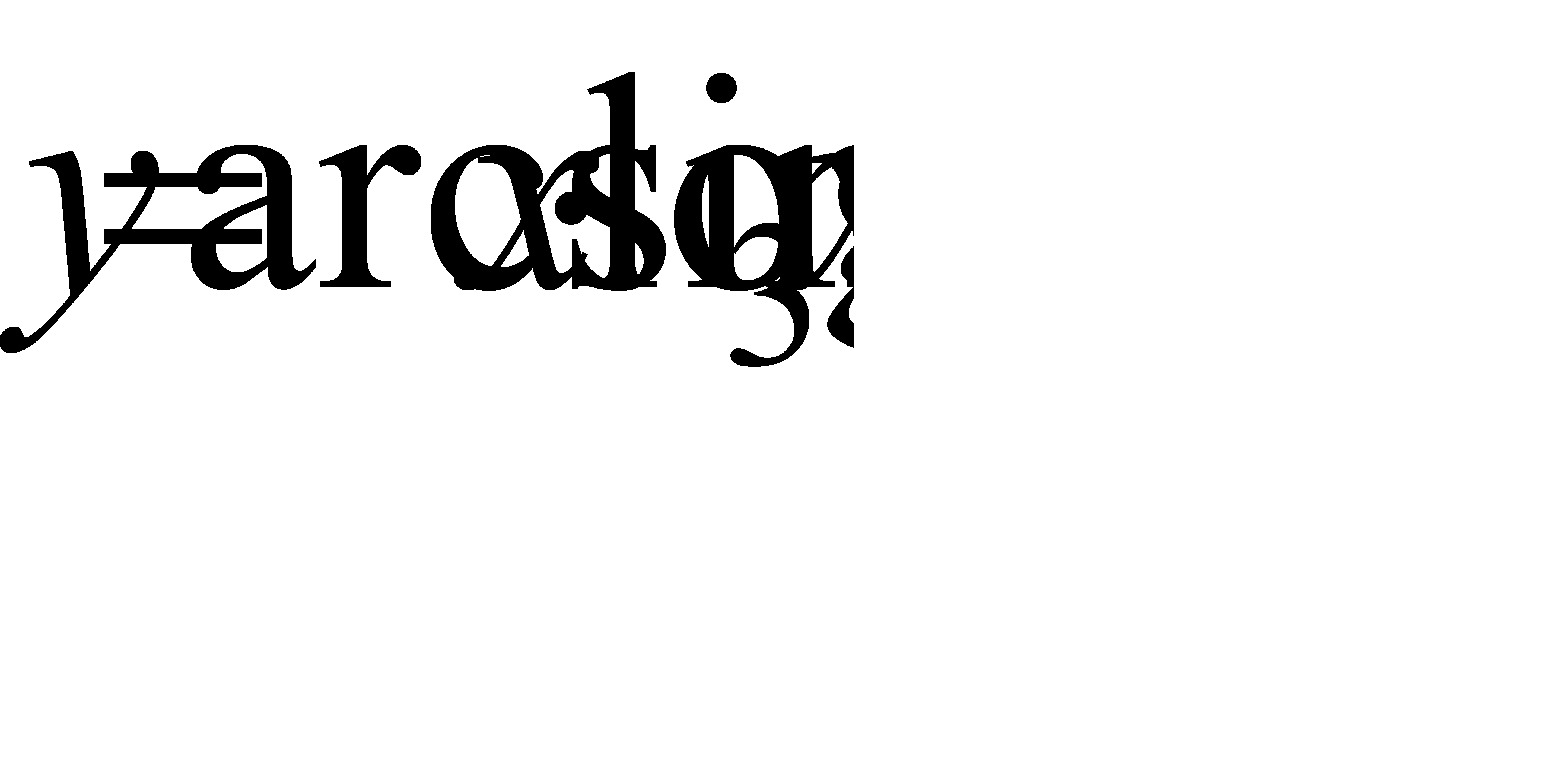 ; б)
; б) 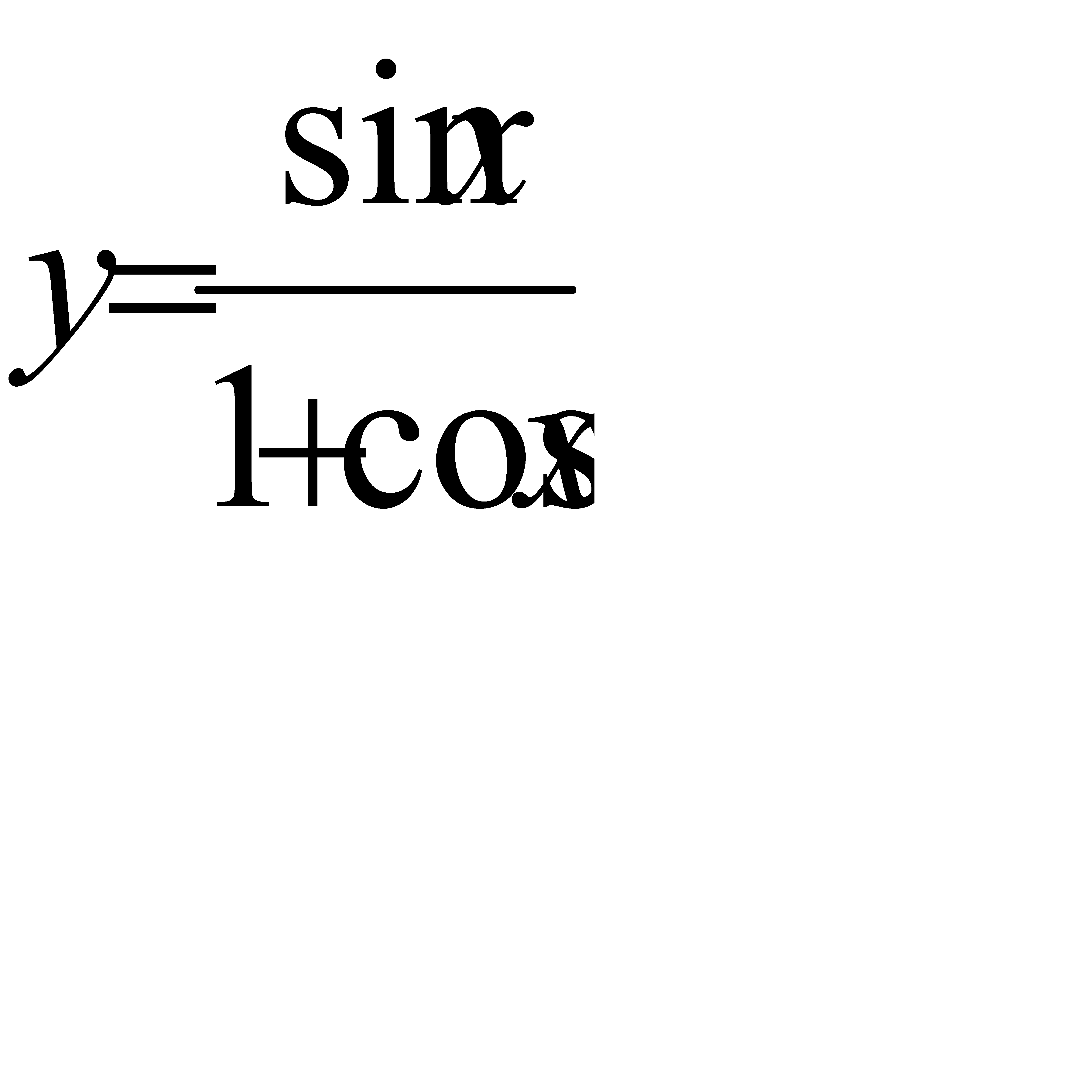 ; г)
; г) 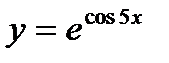 .
.
4.4 а) 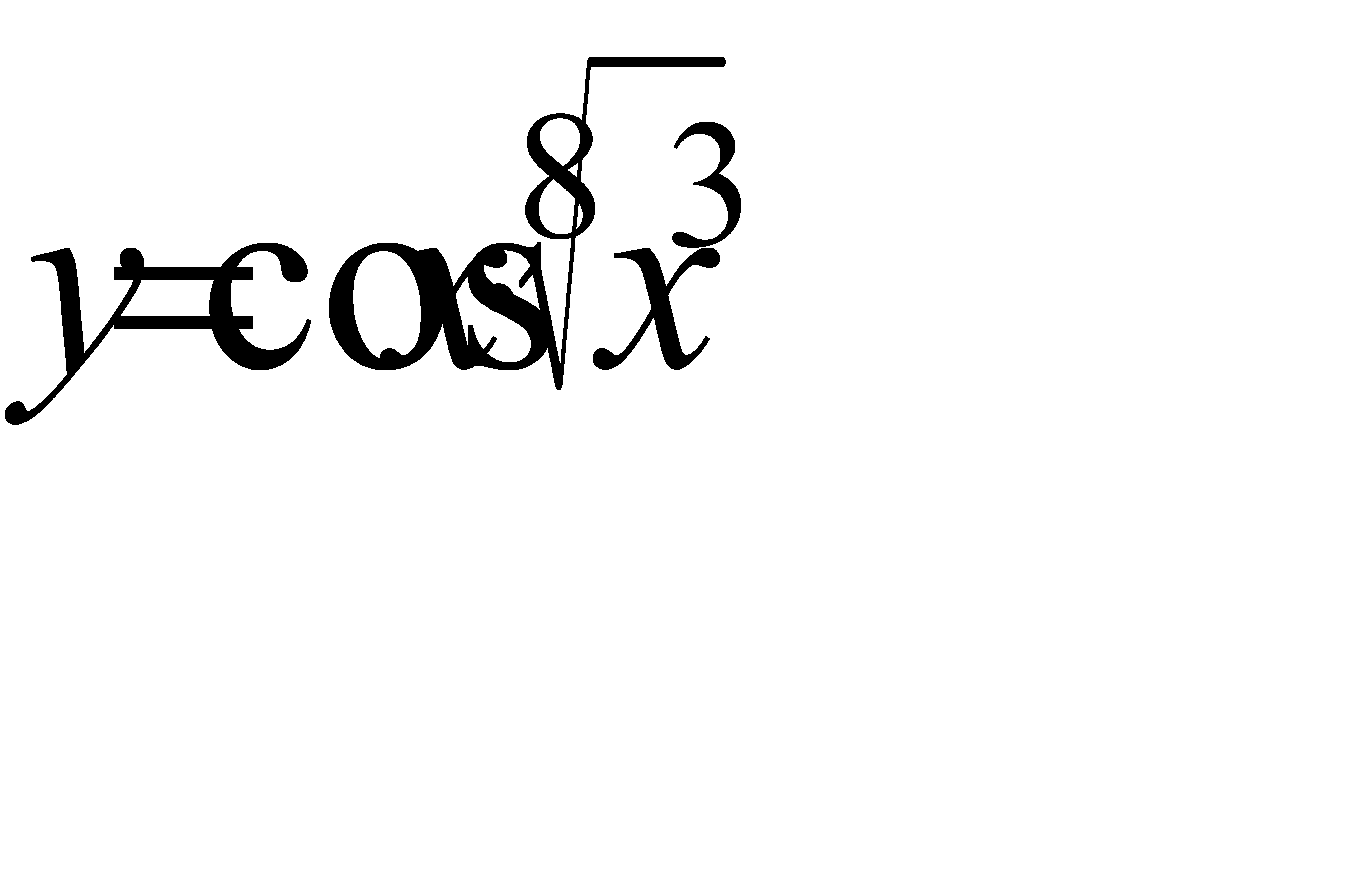 ; б)
; б) 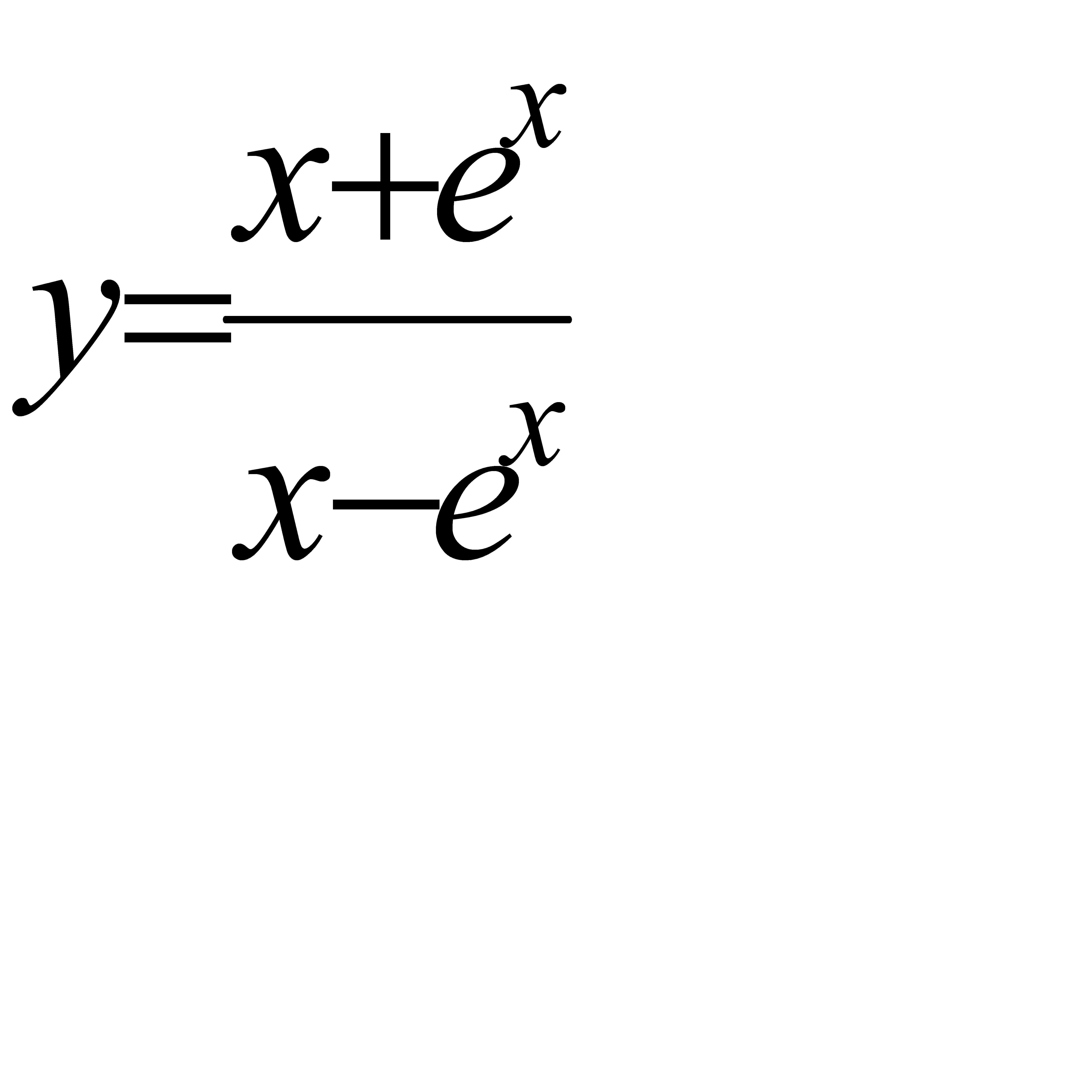 ; в)
; в) 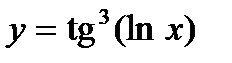 .
.
4.5 а) 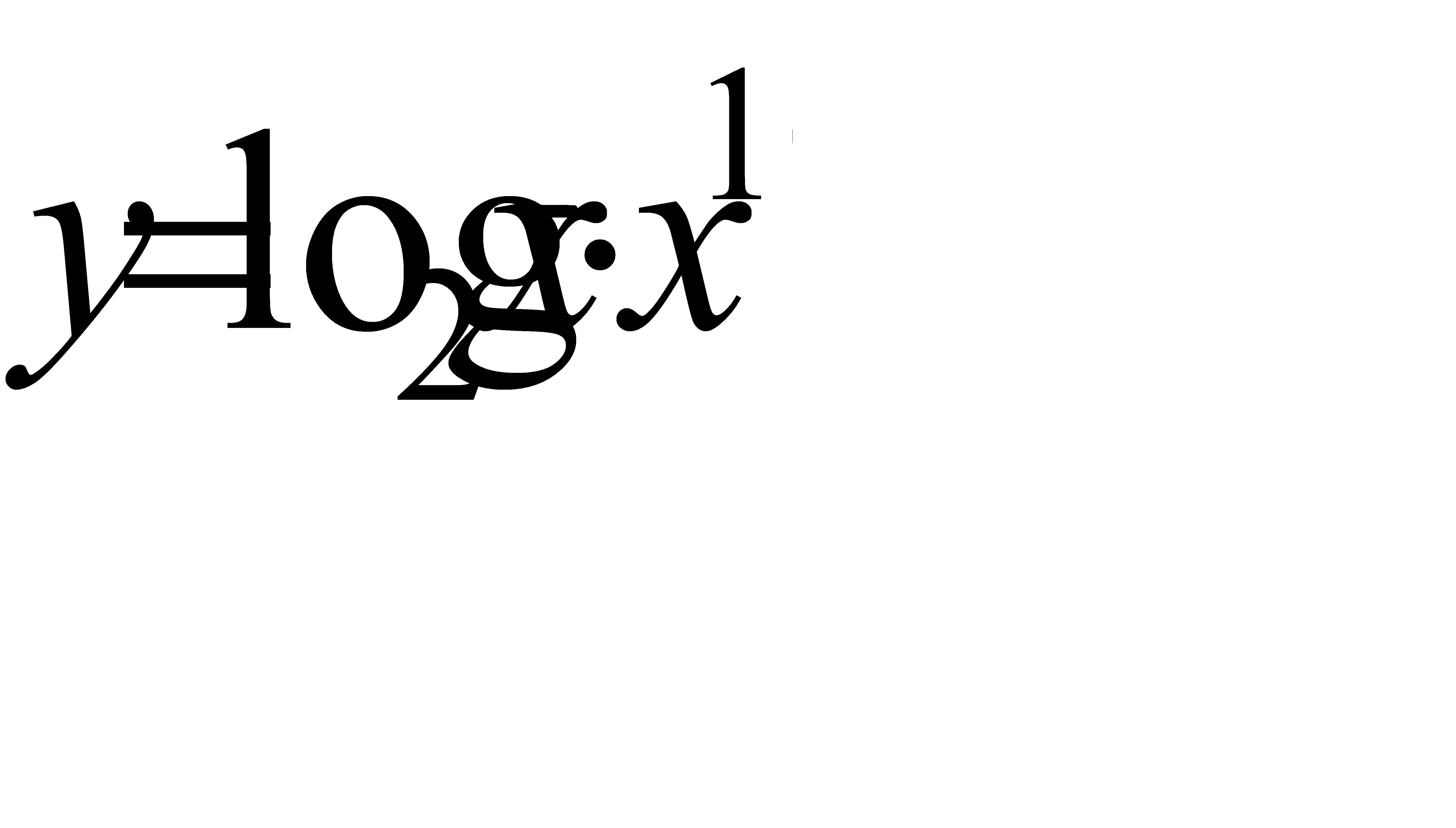 ; б)
; б) 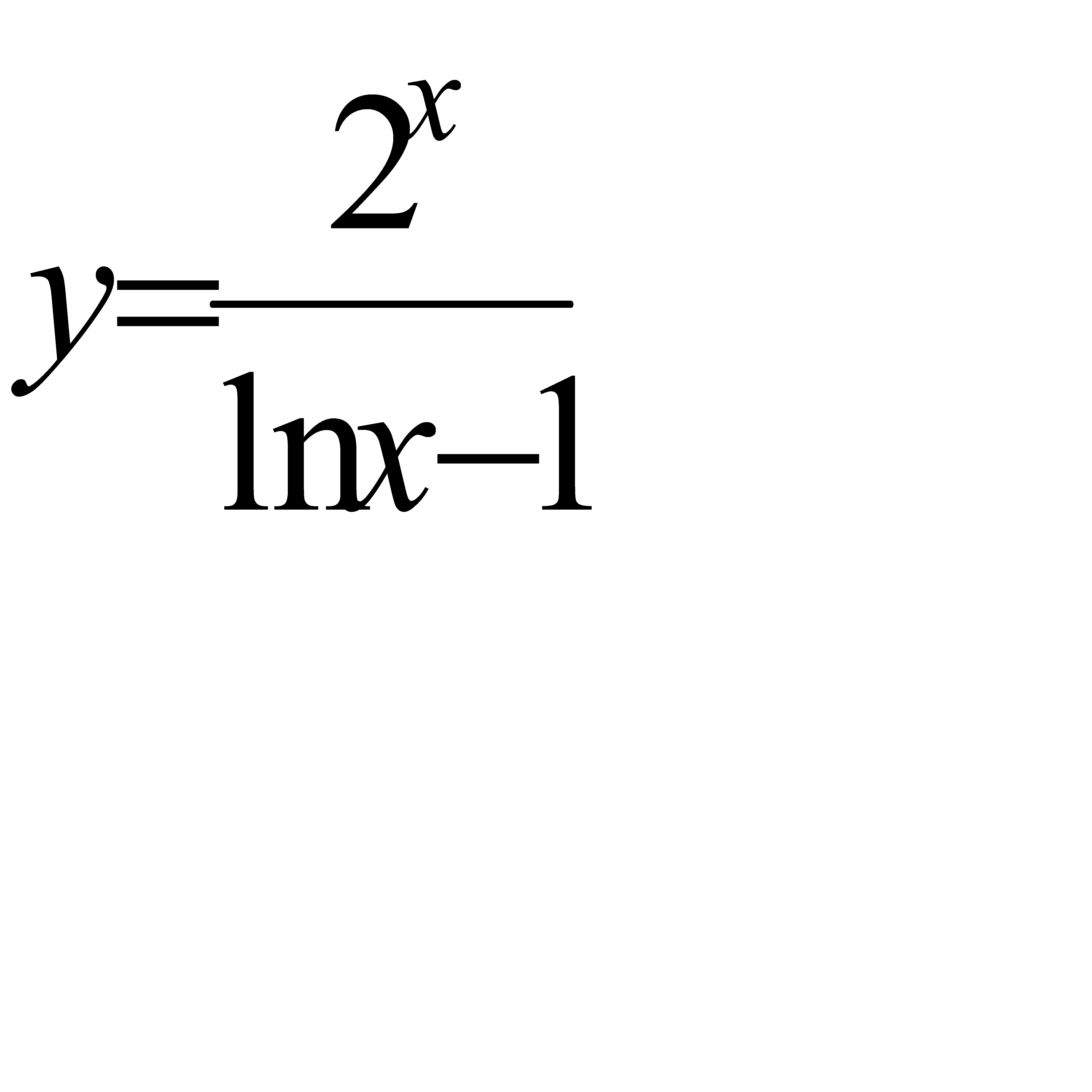 ; в)
; в) 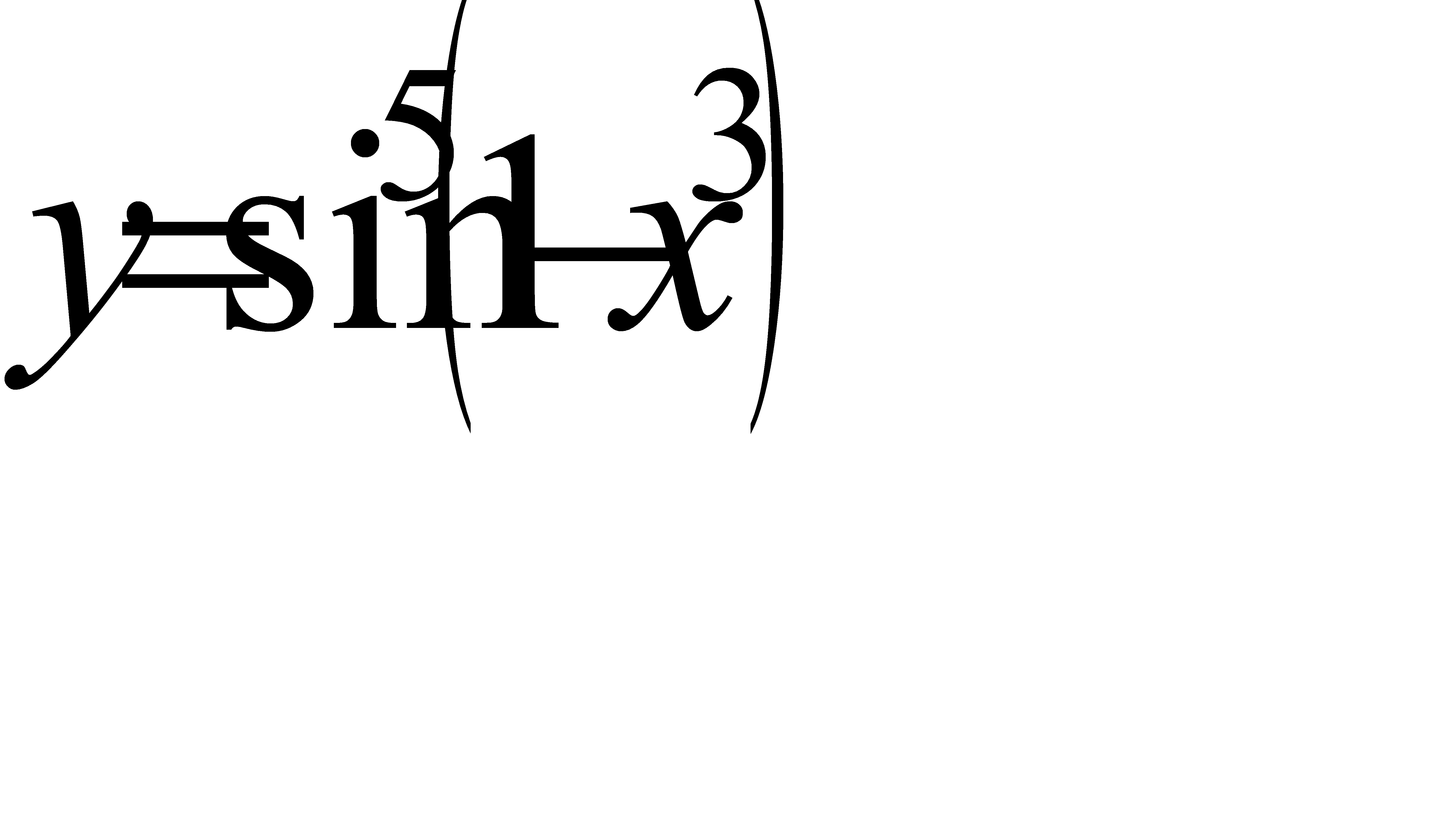 .
.
4.6 а) 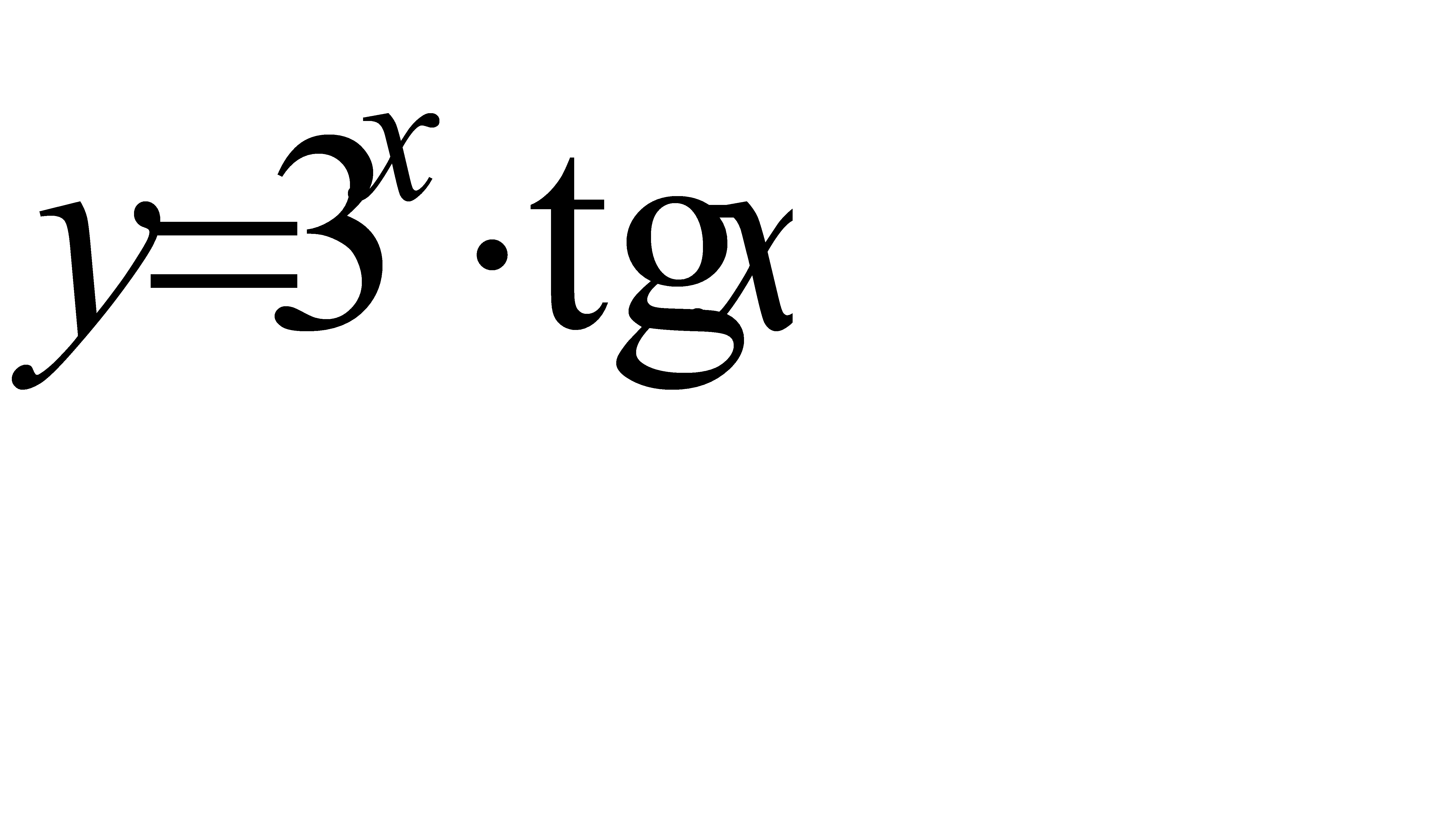 ; б)
; б) 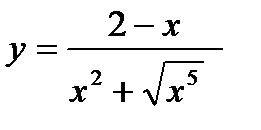 ; г)
; г) 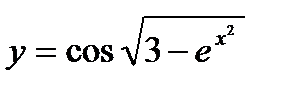 .
.
4.7 а) 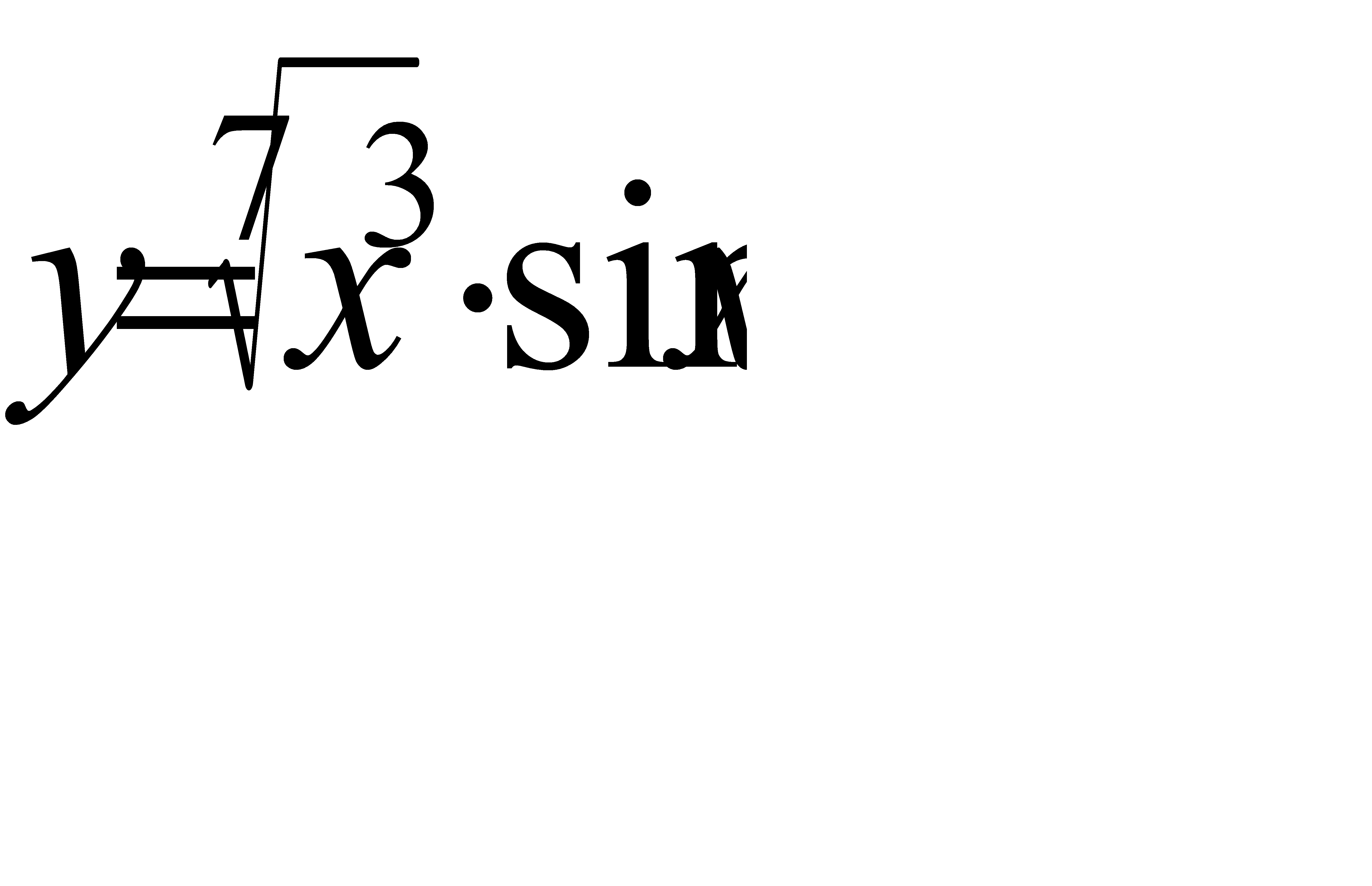 ; б)
; б) 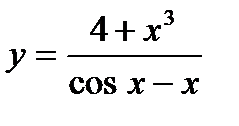 ; в)
; в) 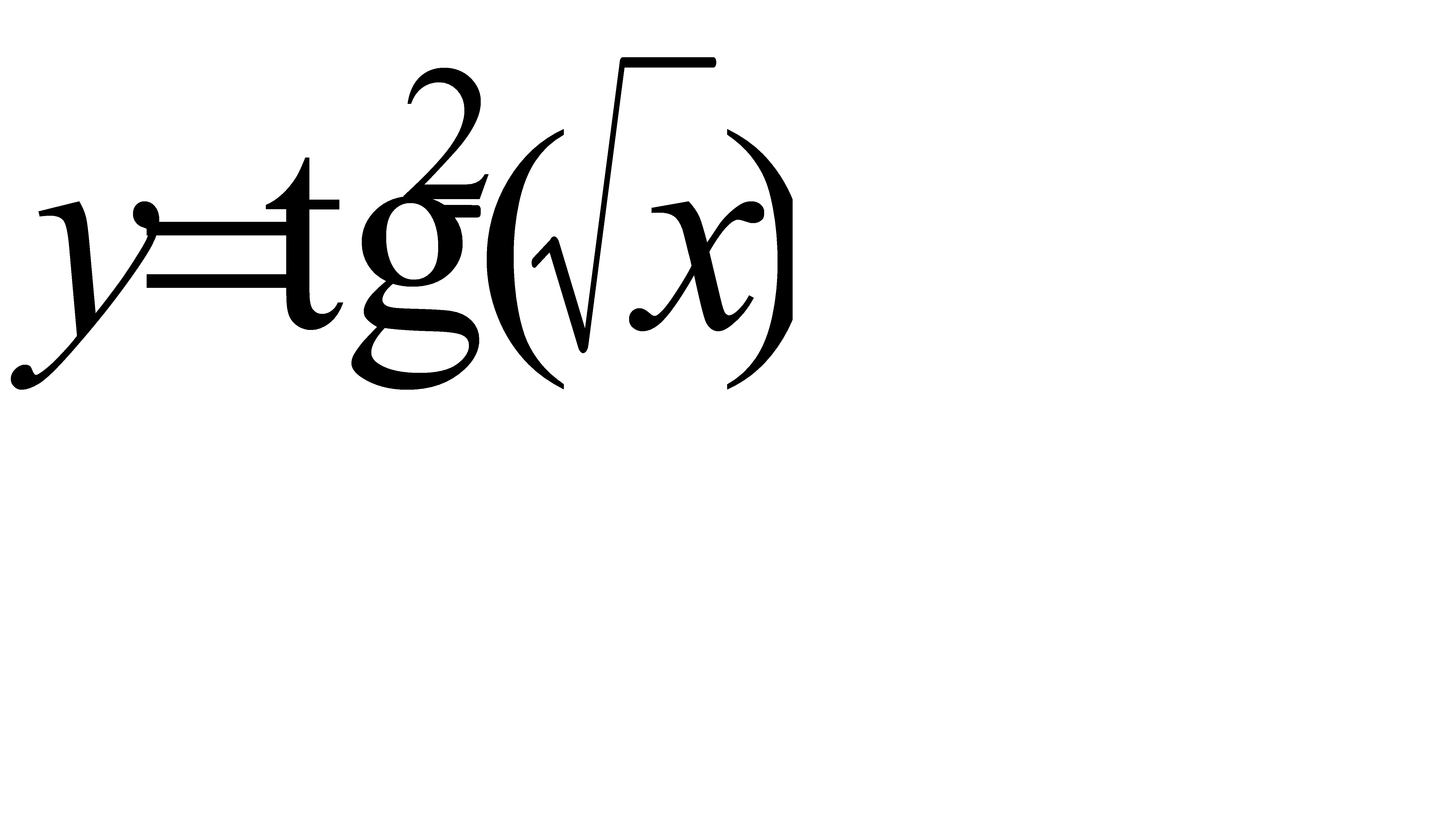 .
.
4.8 а) 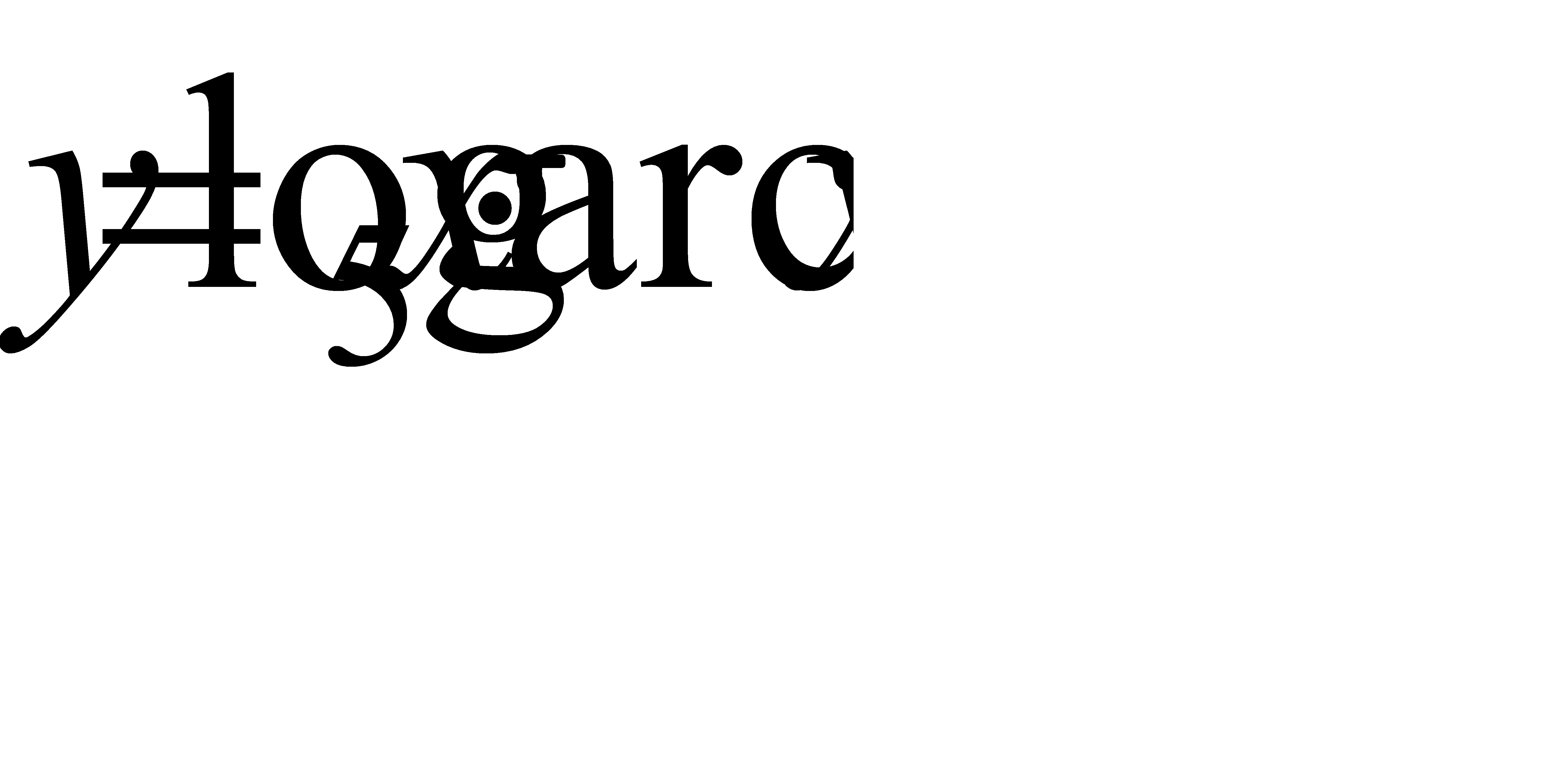 ; б)
; б) 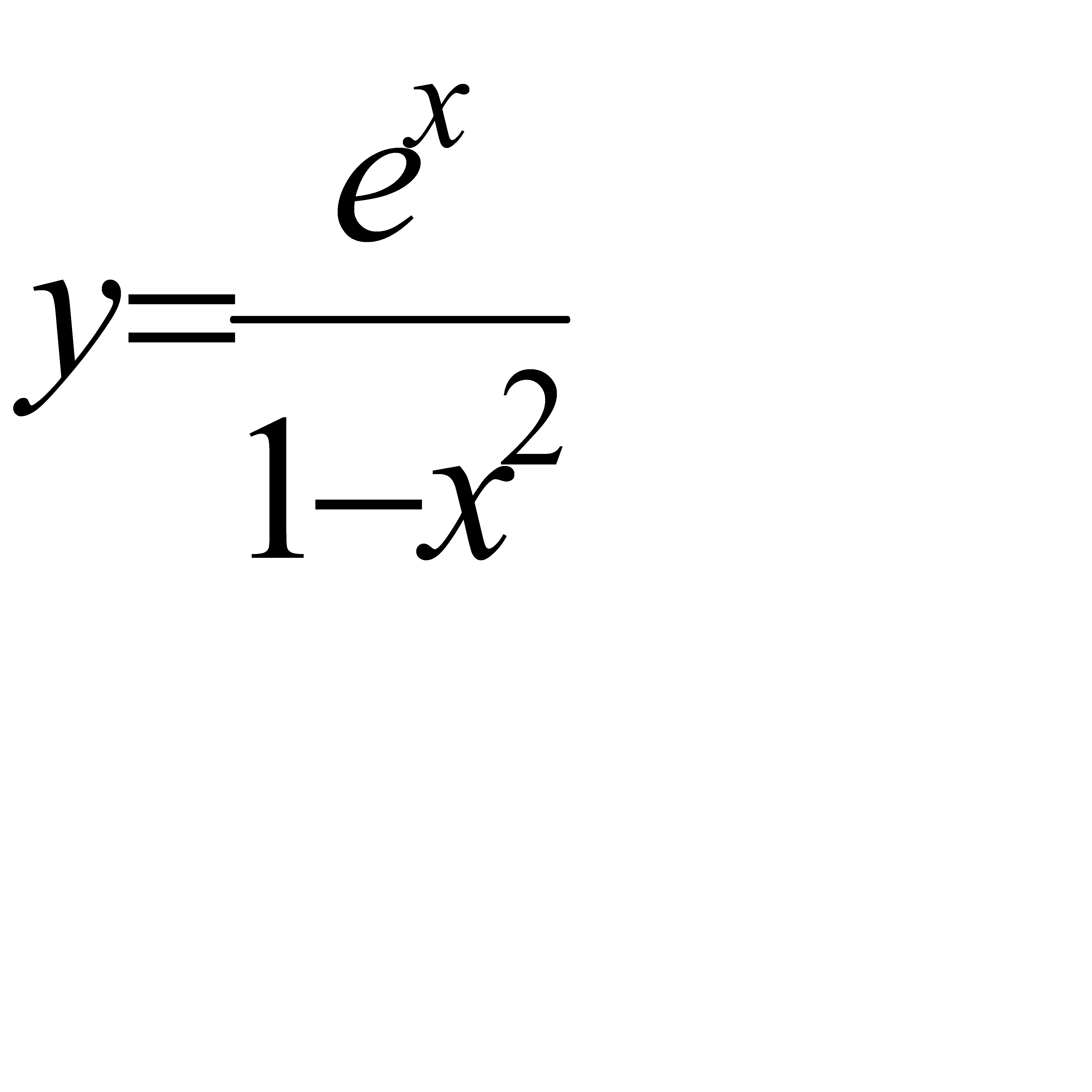 ; в)
; в) 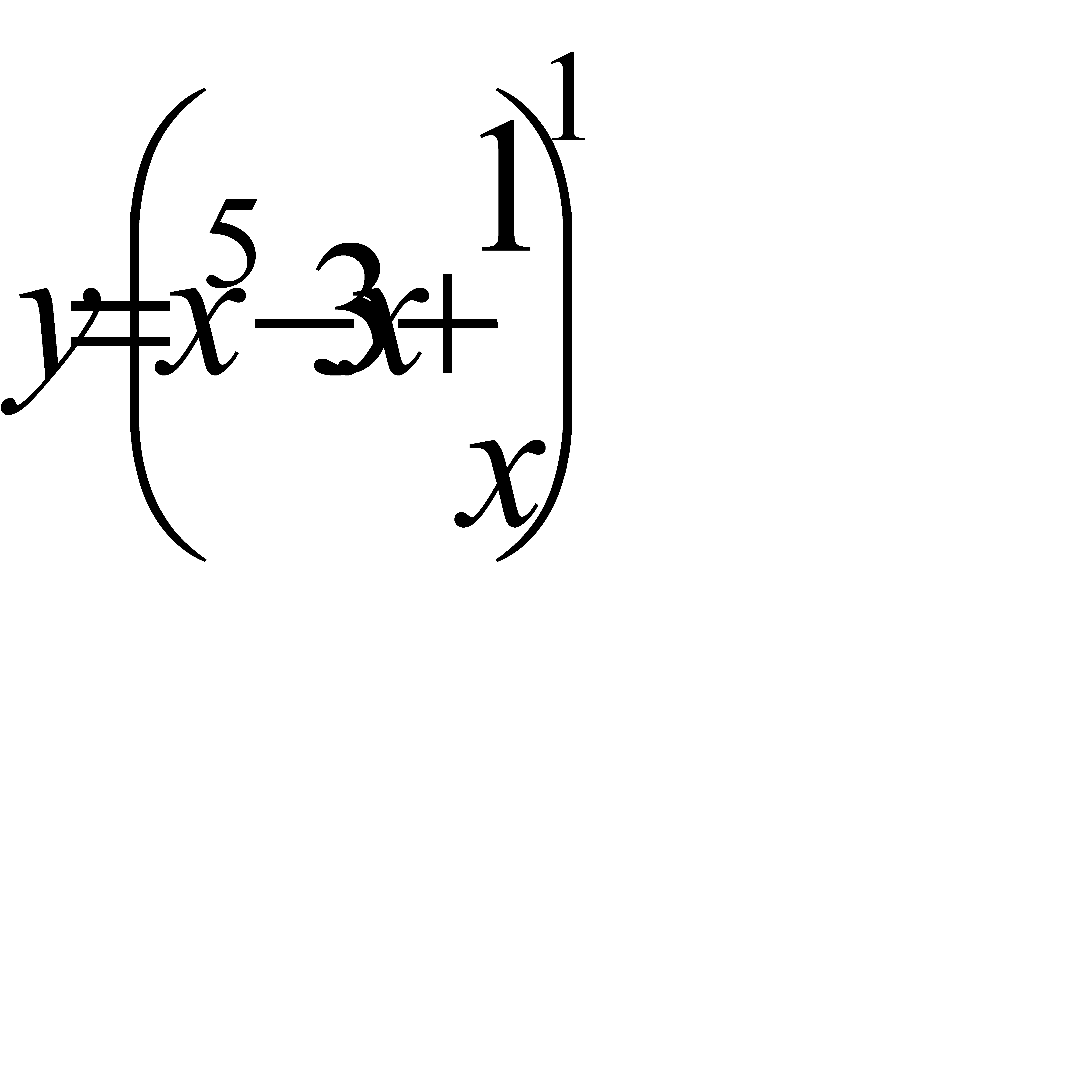 .
.
4.9 а) 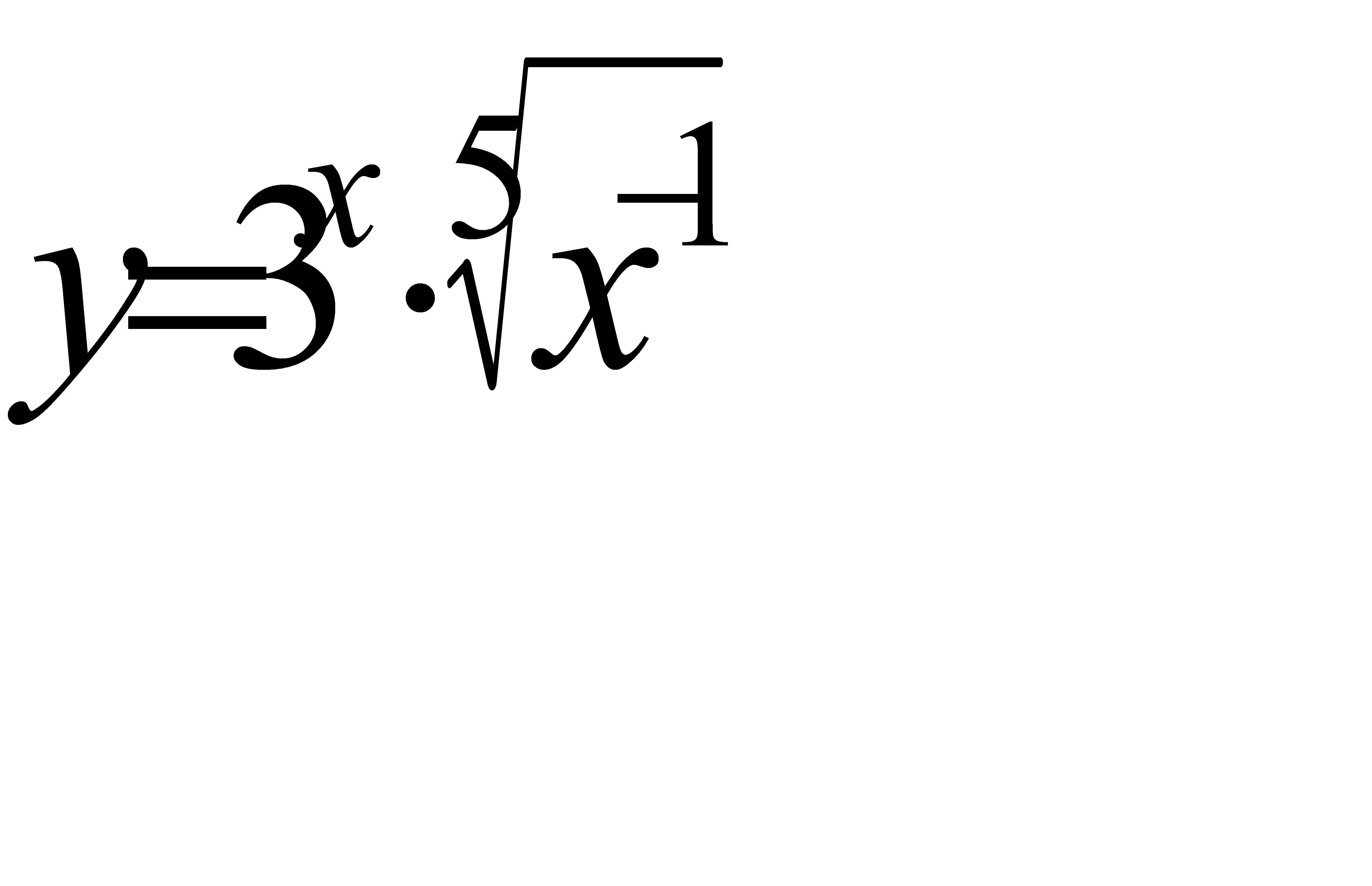 ; б)
; б) 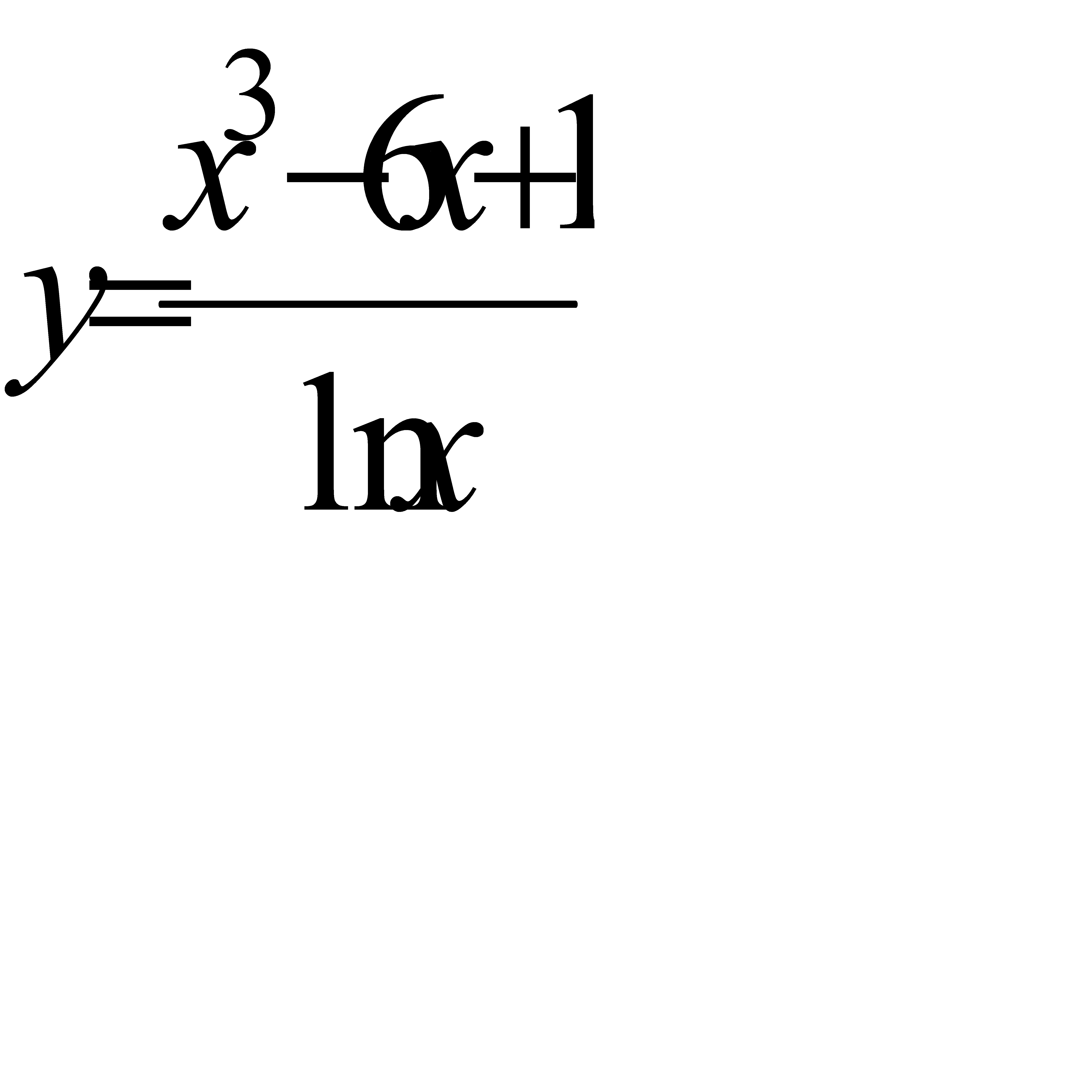 ; в)
; в) 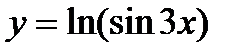 ;
;
4.10 а) 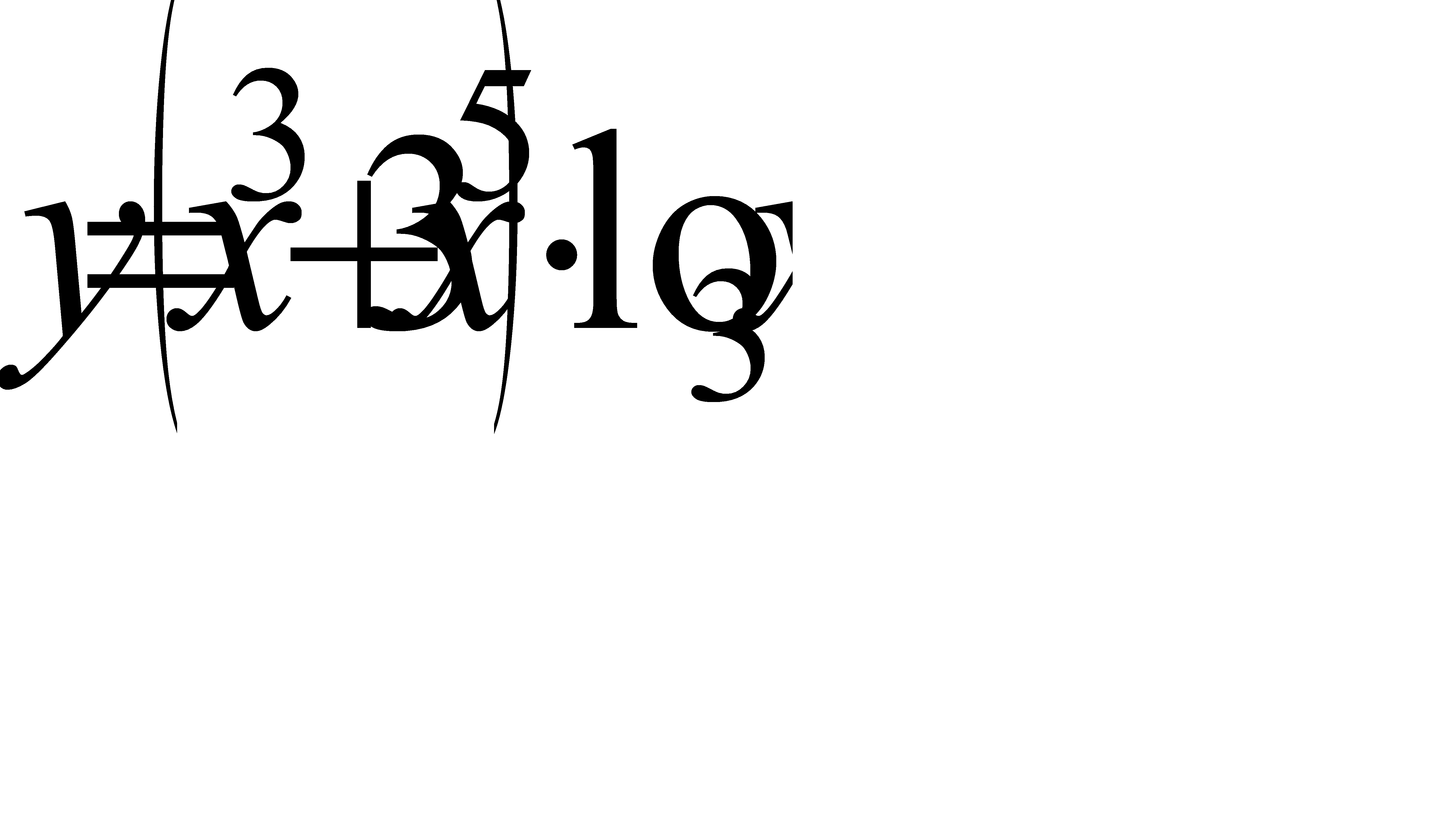 ; б)
; б) 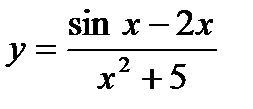 ; г)
; г) 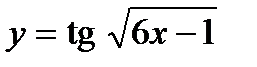 .
.
ЗАДАНИЕ 5
Провести полное исследование функций и построить их графики.
5.1. y=4x3 +15x2 +12x+1
5.2. y=-x3+3x2+9x-12
5.3. y=3x3-x+2
5.4. y=x4-8x2+16
5.5. y=x3-6x2+9x-3
5.6. y=  x3-x
x3-x
5.7. y=-x4+2x2+3
5.8. y=  x3-x2+1
x3-x2+1
5.9. а) 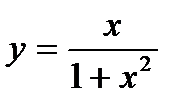
5.10.y=x3-3x2+1
ЗАДАНИЕ 6
Вычислить неопределённые интегралы. В пунктах а) и б) результаты проверить дифференцированием.
6.1 а) 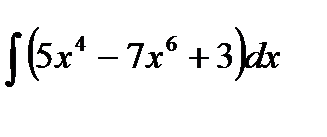 ; б)
; б) 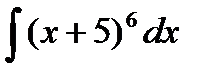 ;
;
в) 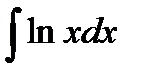 .
.
6.2 а) 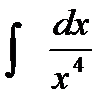 ; б)
; б) 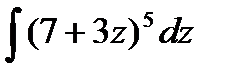 ;
;
в) 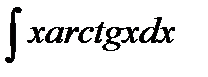 .
.
6.3 а) 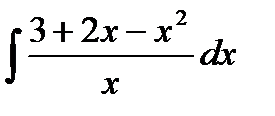 ; б)
; б) 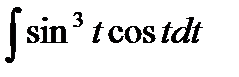 ;
;
в) 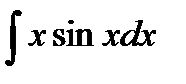 .
.
6.4 а) 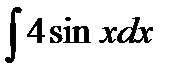 ; б)
; б) 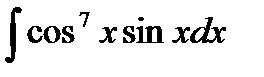 ;
;
в) 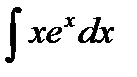
6.5 а) 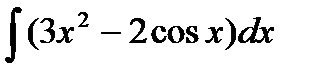 ; б)
; б) 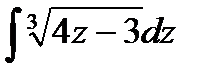 ;
;
в) 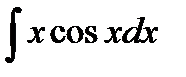 .
.
6.6 а) 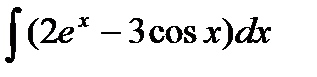 ; б)
; б) 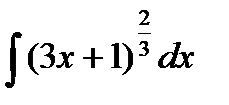 ;
;
в) 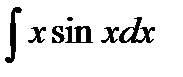 /
/
6.7 а) 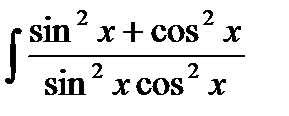 ; б)
; б) 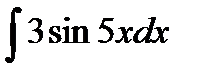 ;
;
в) 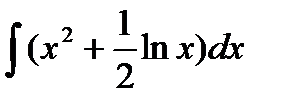 ;
;
6.8 а) 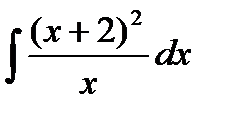 ; б)
; б) 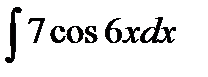 ;
;
в) 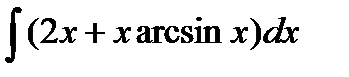 .
.
6.9 а) 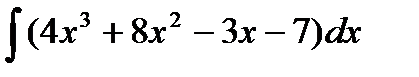 ; б)
; б) 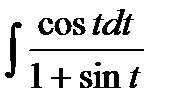 ;
;
в) 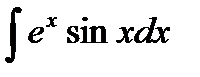 .
.
6.10 а) 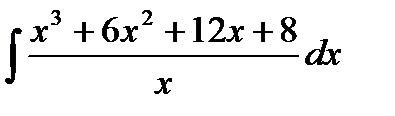 ; б)
; б) 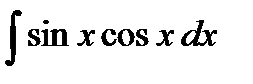 ;
;
в) 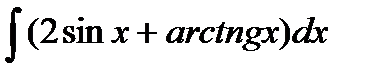 .
.
ЗАДАНИЕ 7
Вычислить приближённое значение определённого интеграла 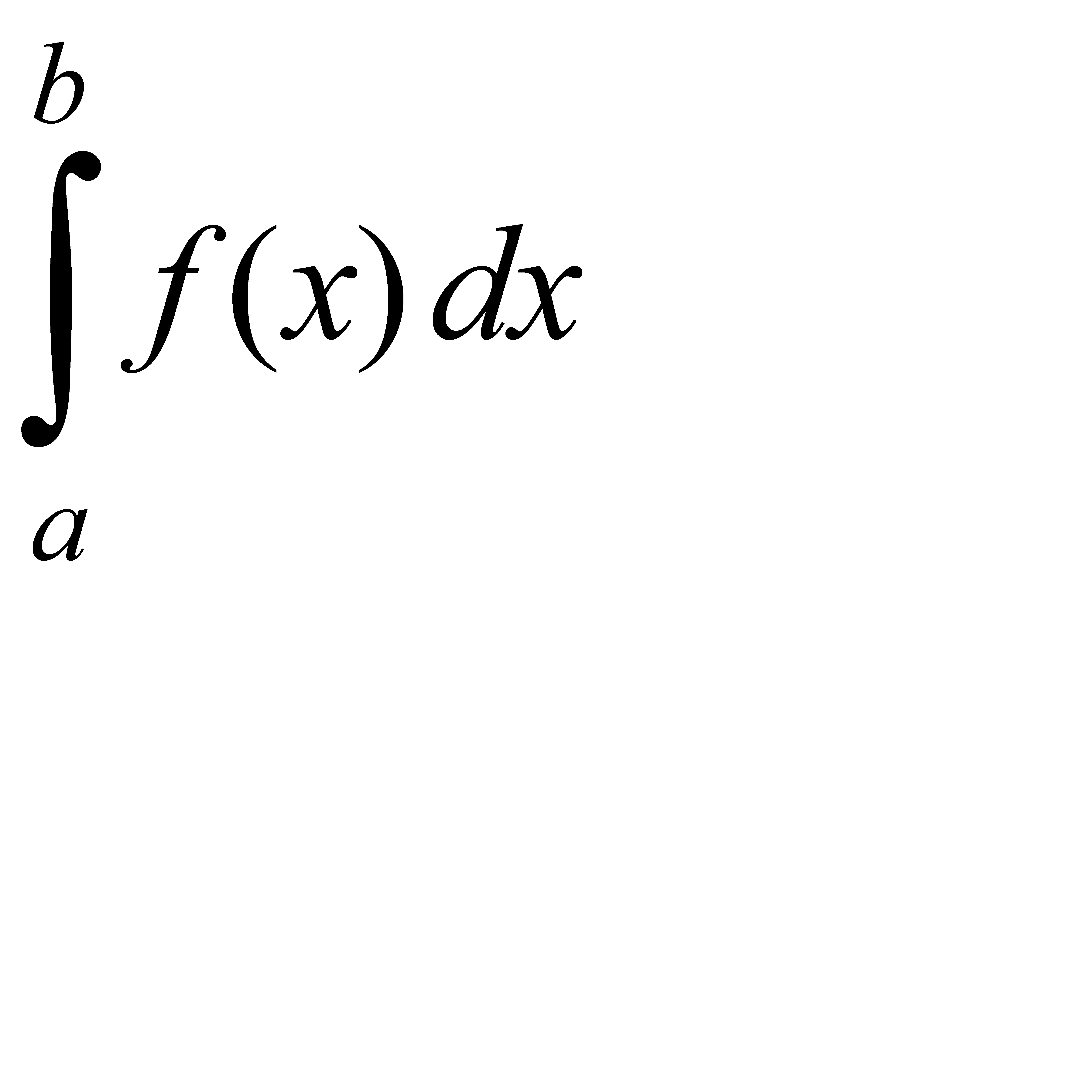 с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
7.1 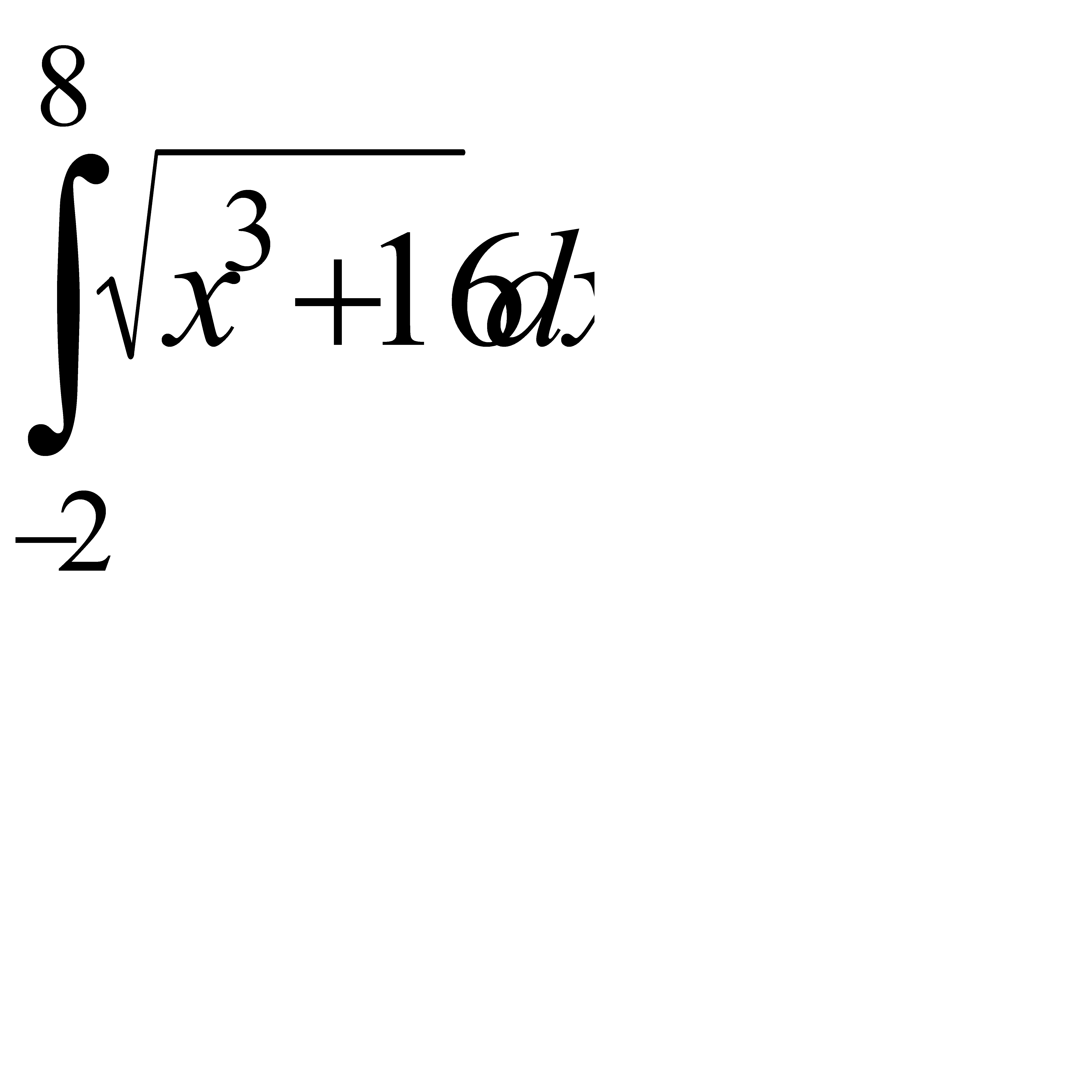 . 7.2
. 7.2 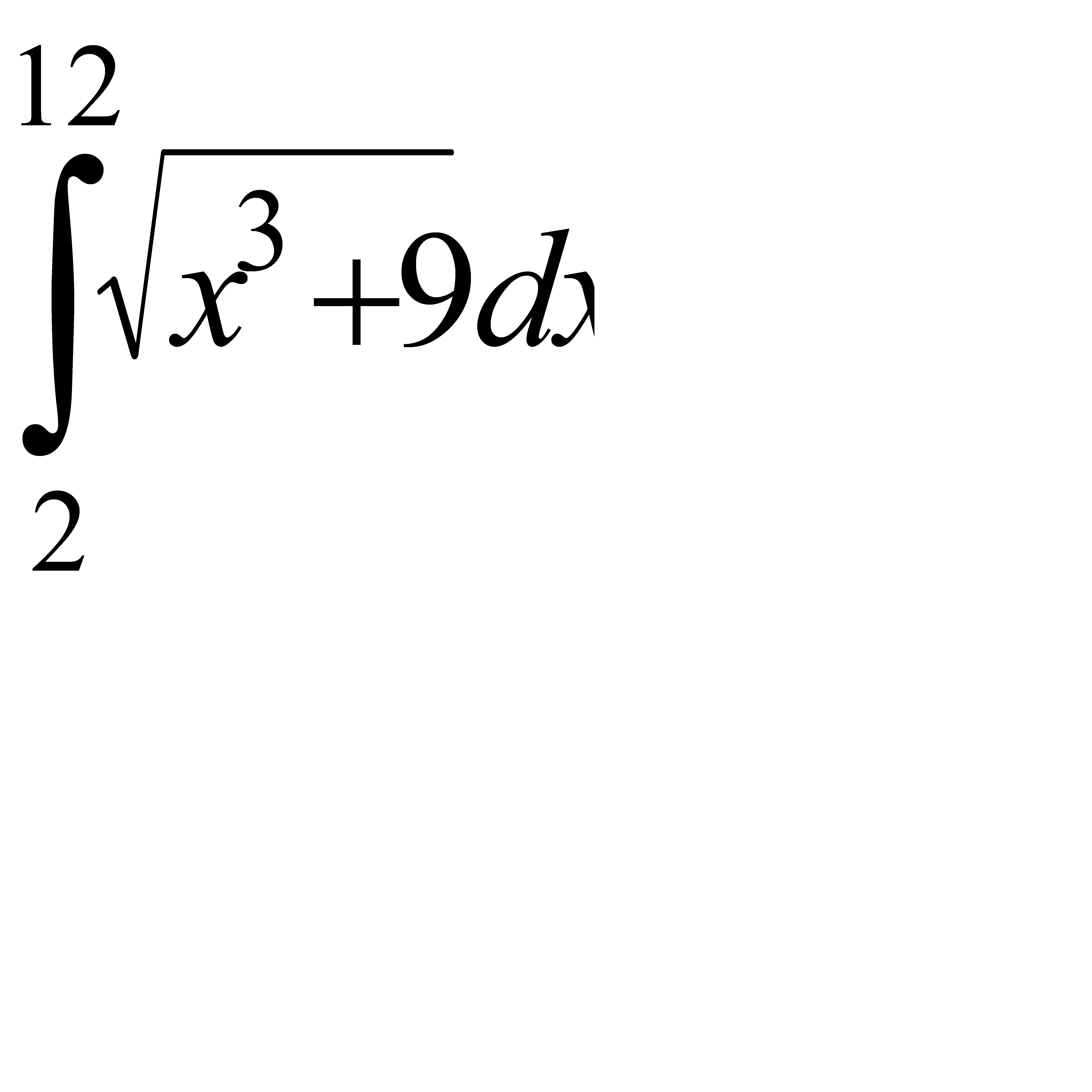 .
.
7.3 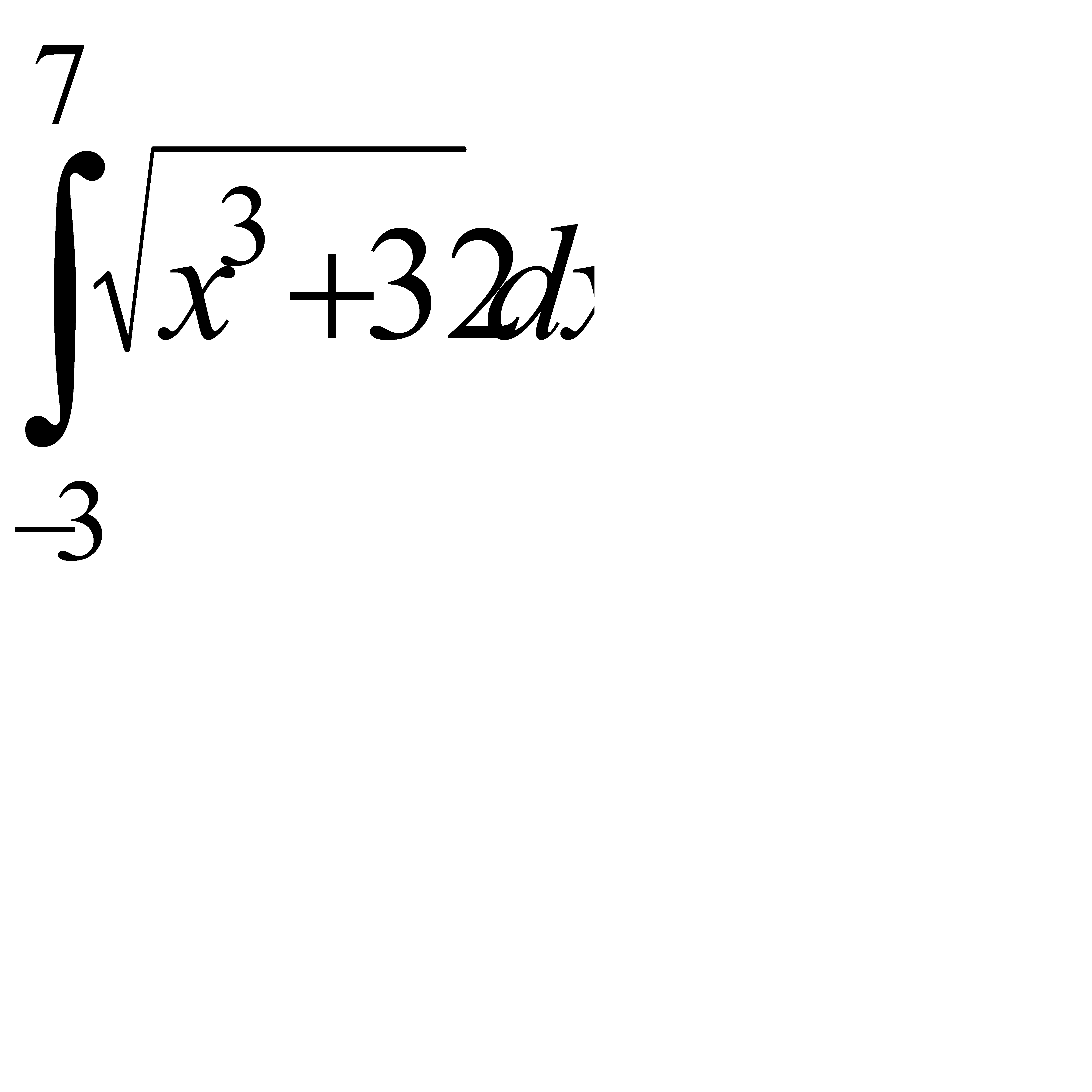 . 7.4
. 7.4 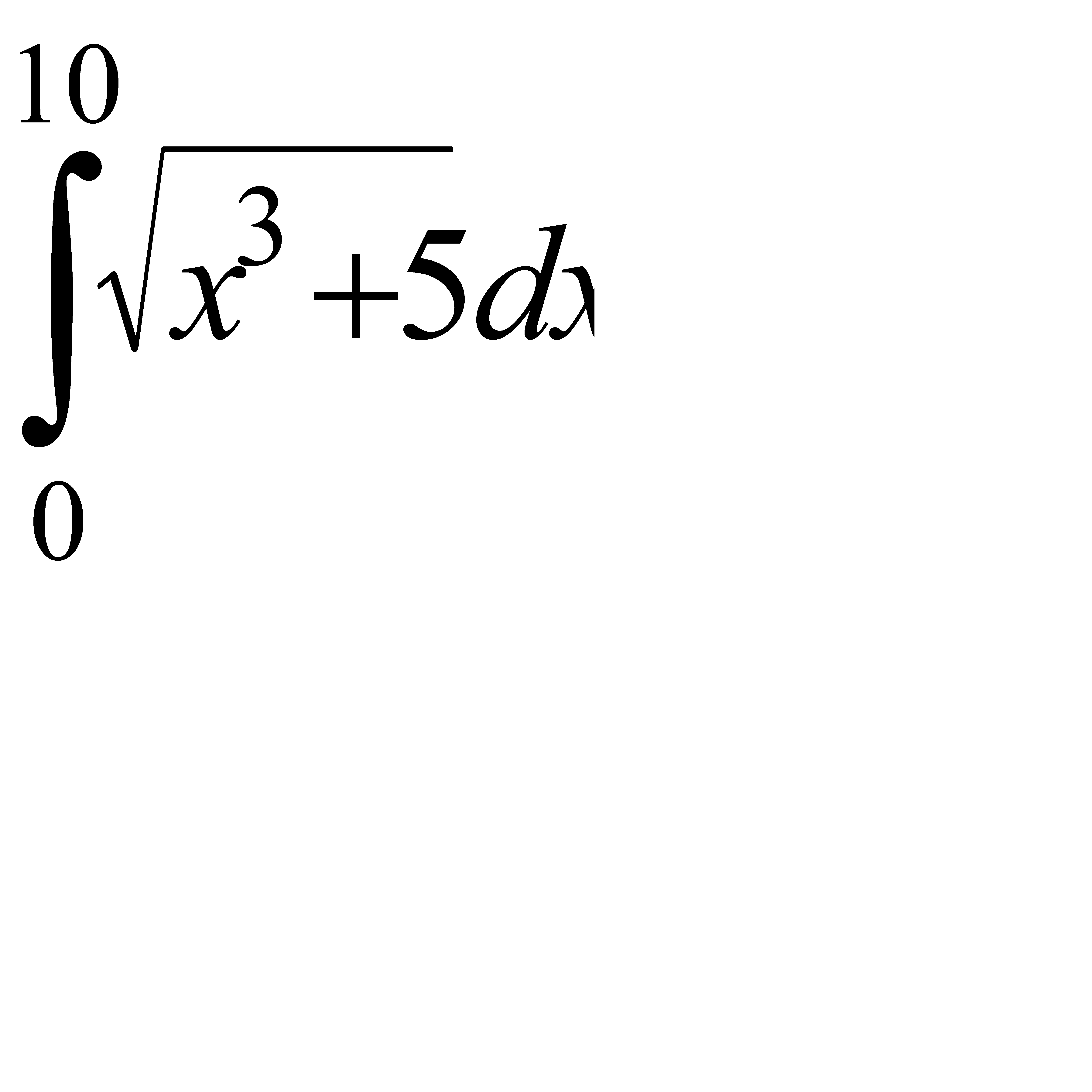 .
.
7.5 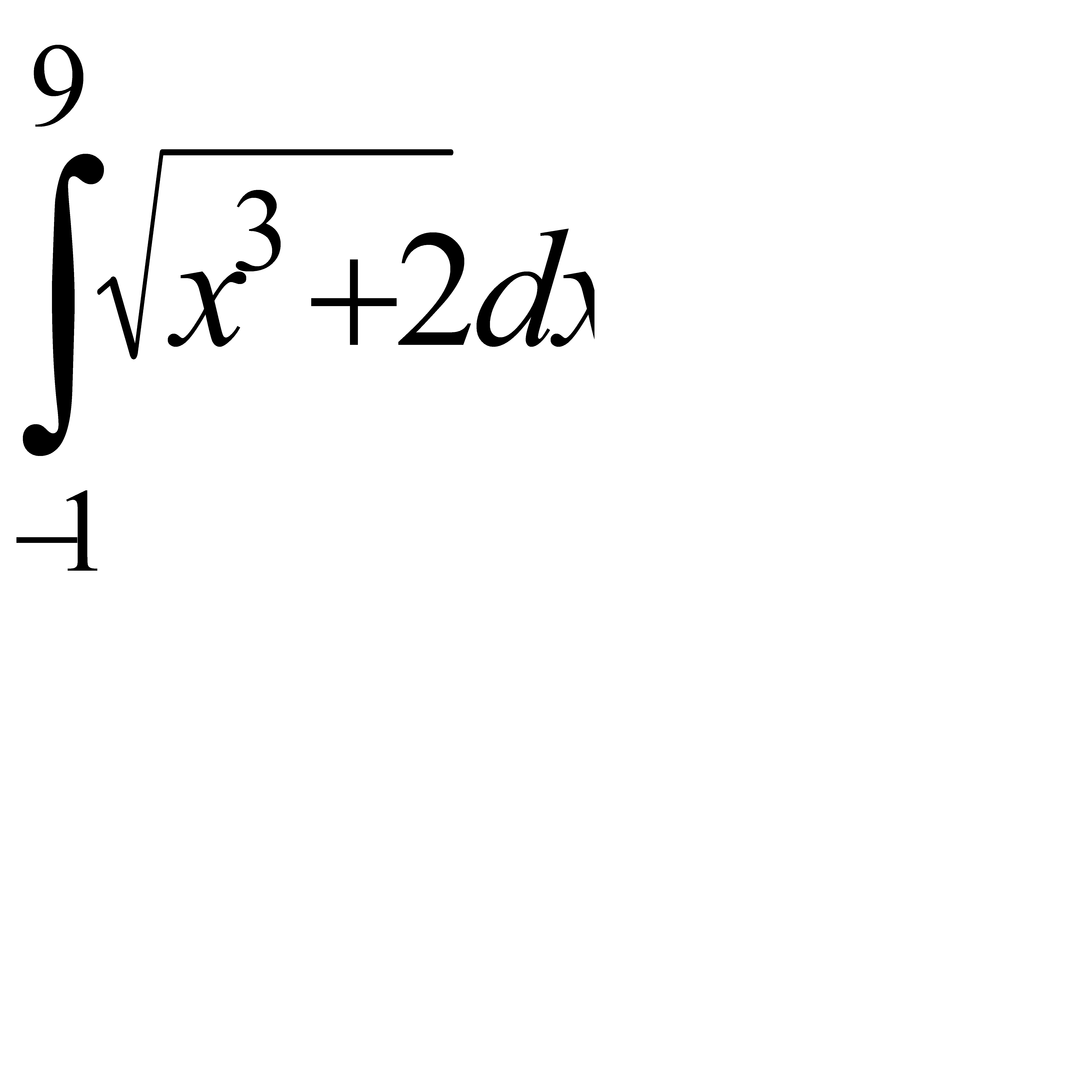 . 7.6
. 7.6 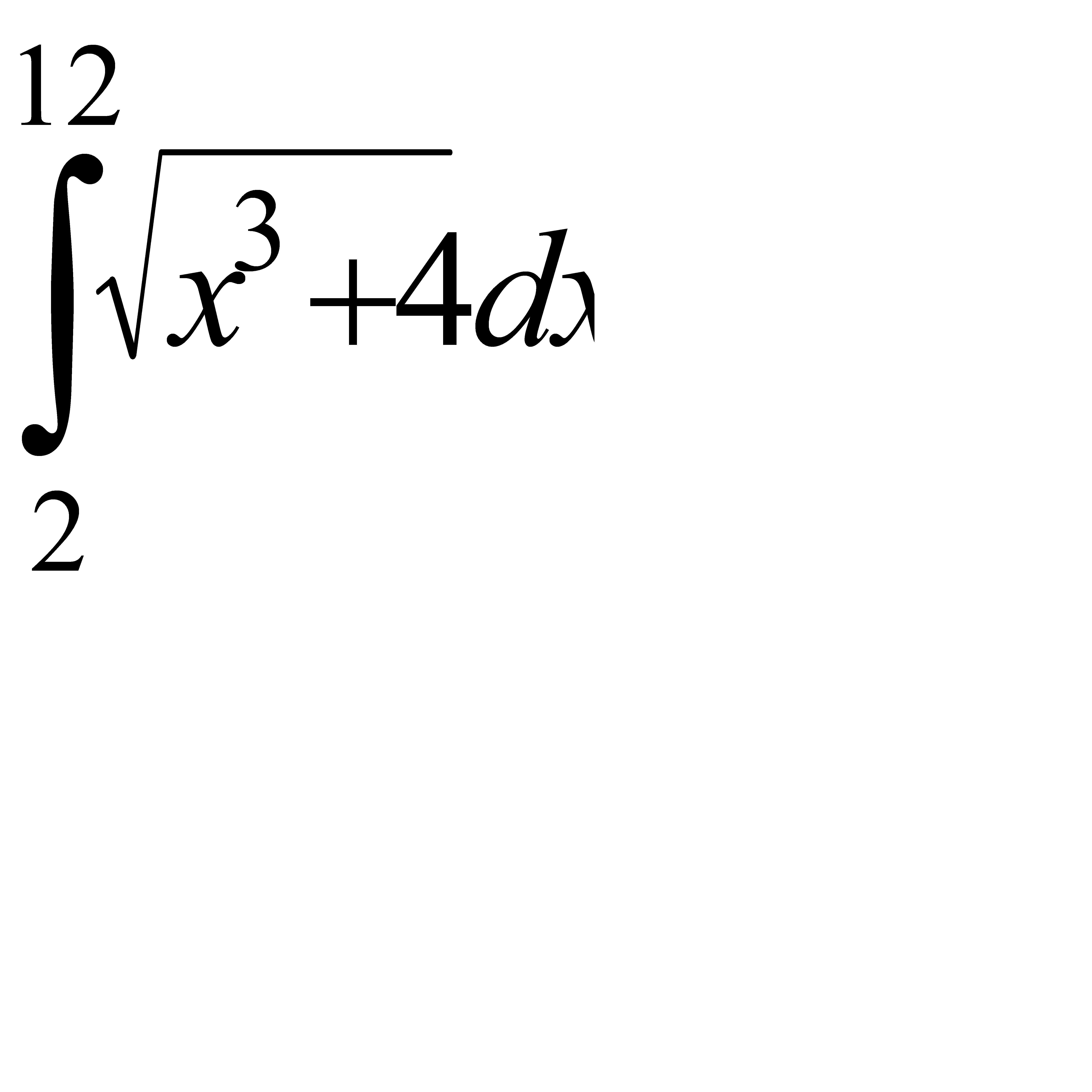 .
.
7.7 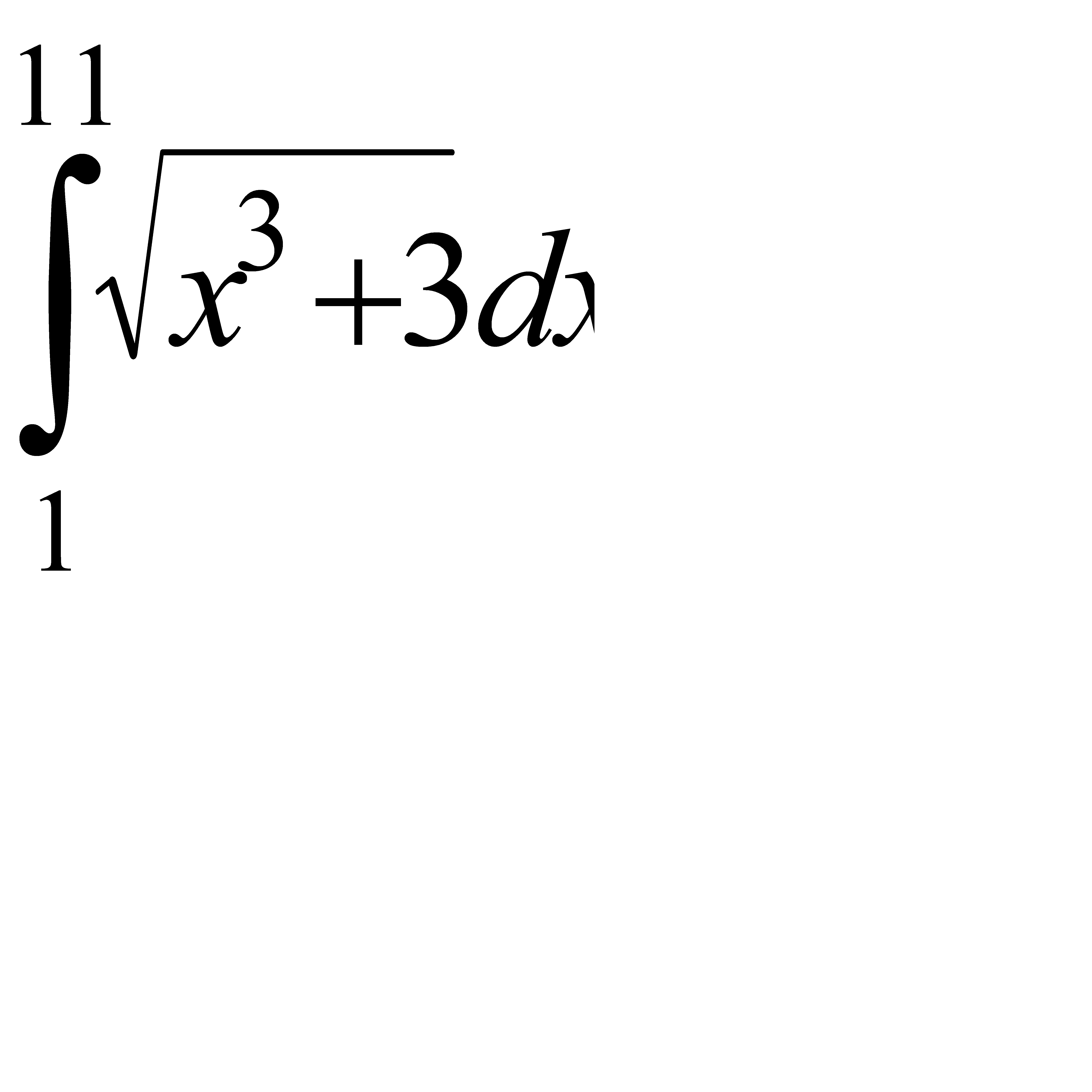 . 7.8
. 7.8 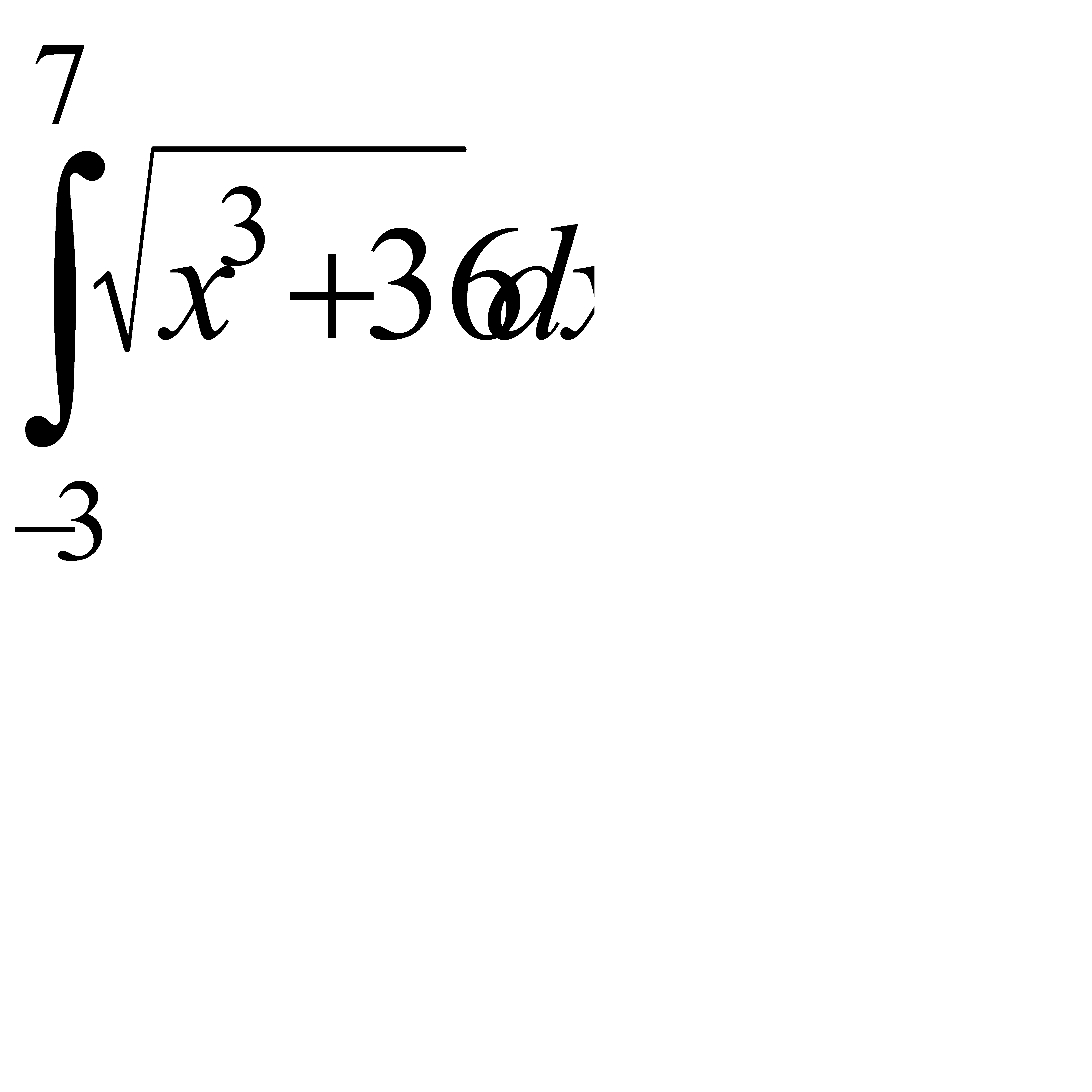 .
.
7.9 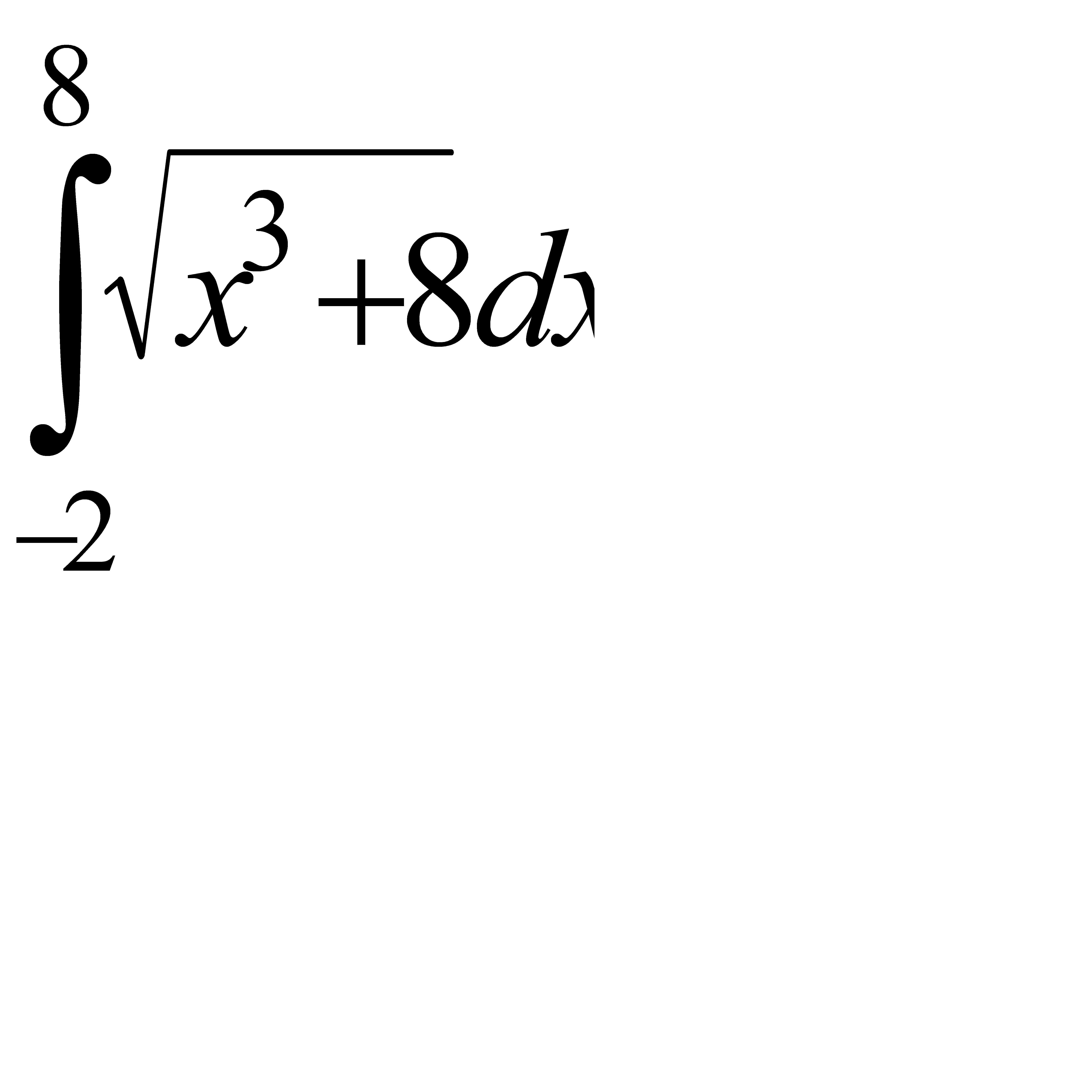 . 7.10
. 7.10 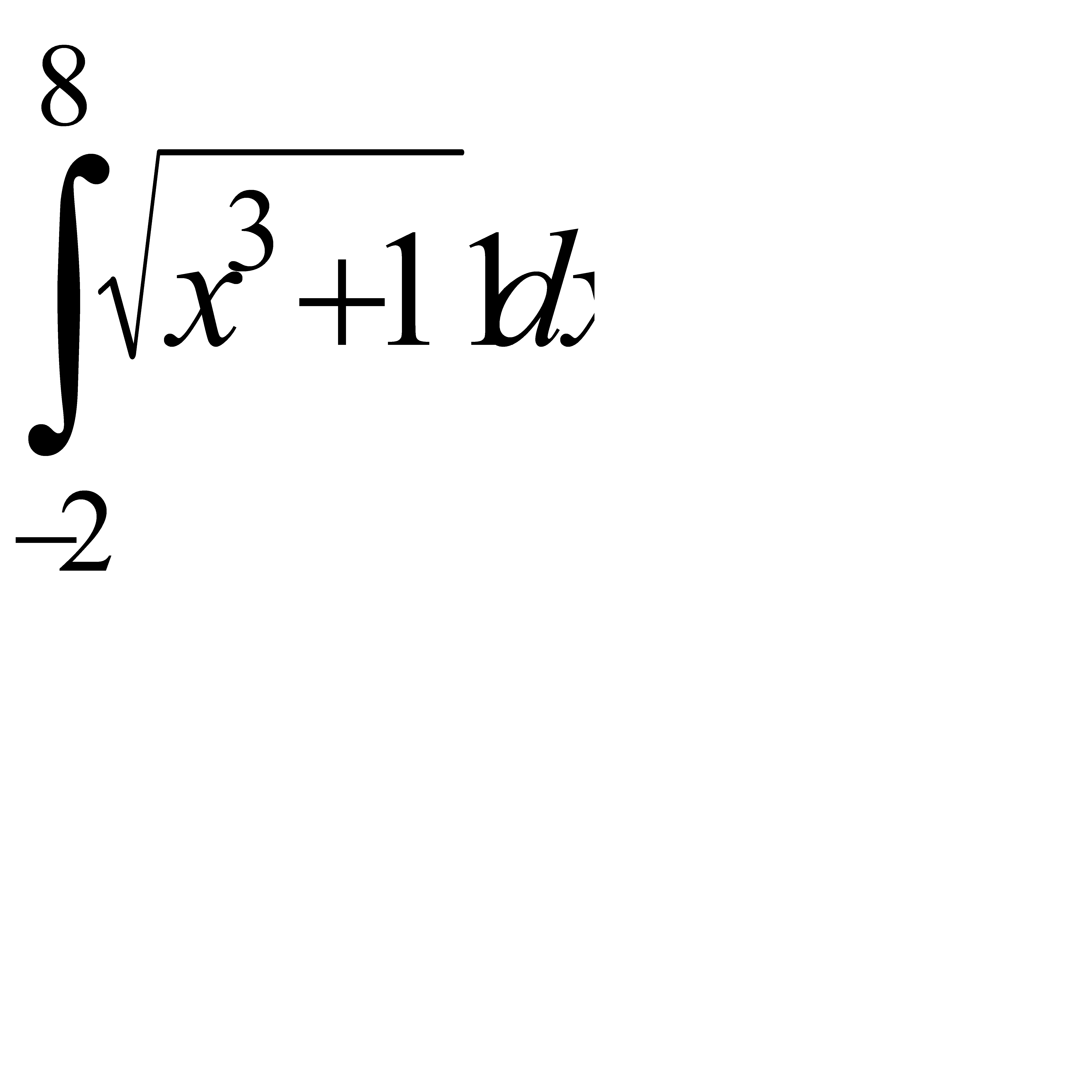 .
.
ЗАДАНИЕ 8
Вычислить определенный интеграл используя формулы Ньютона - Лейбница.
8.1 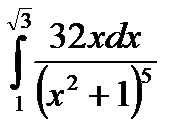 . 8.2
. 8.2 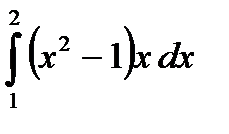 .
.
8.3 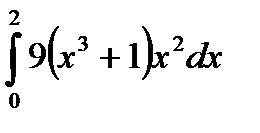 . 8.4
. 8.4 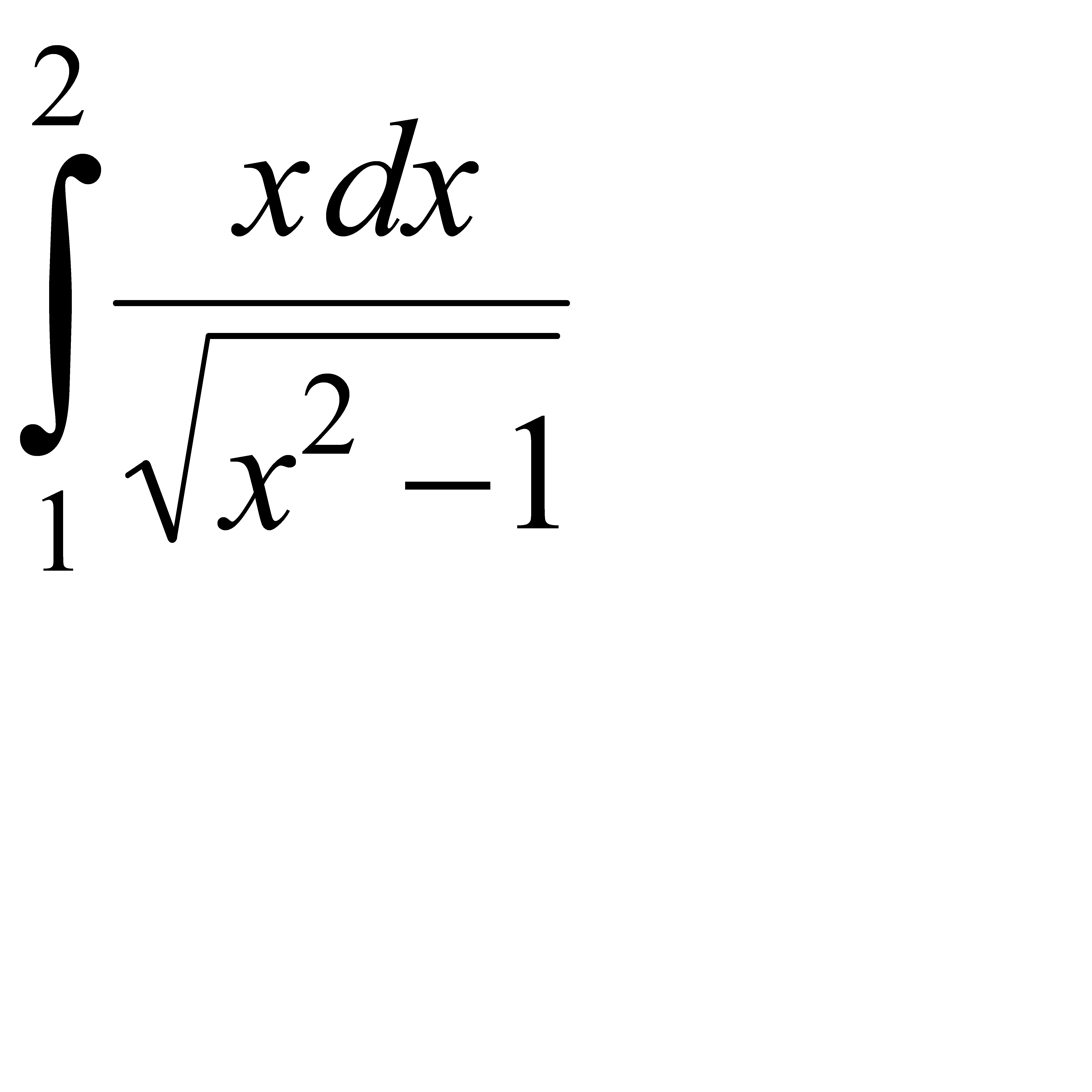 .
.
8.5 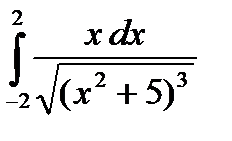 . 8.6
. 8.6 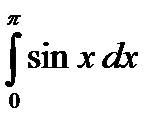 .
.
8.7 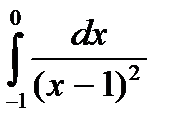 . 8.8
. 8.8 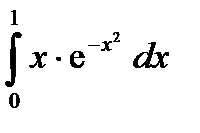 .
.
8.9 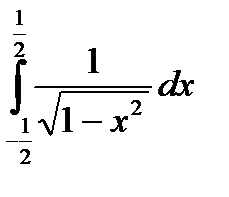 . 8.10
. 8.10 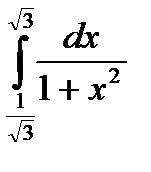 .
.
ЗАДАНИЕ 9
9 .1. Вычислить площадь фигуры, ограниченной параболой 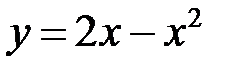 и прямой
и прямой 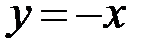 .
.
9.2. Вычислить площадь фигуры, ограниченной линиями
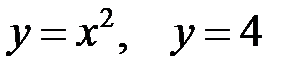 .
.
9.3. Вычислить площадь фигуры, ограниченной линиями
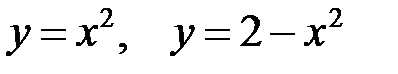 .
.
9.4. Вычислить площадь фигуры, ограниченной параболами
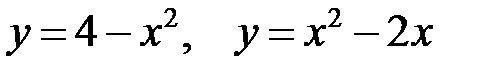 .
.
9.5. Вычислить объём тела, образованного вращением вокруг оси Oxфигуры, ограниченной параболой 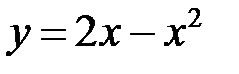 и прямой
и прямой 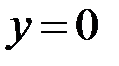 .
.
9.6. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 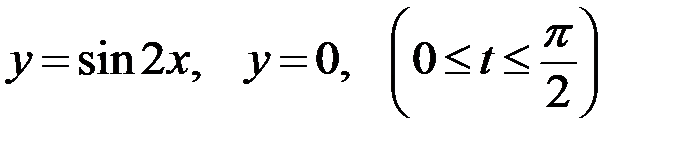 .
.
9.7. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями xy=1, x=2, x=6
9.8. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиямиy=x2, x=0, x=2.
9.9. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями xy=2, x-3=0, x-7=0.
9.10. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиямиy= 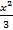 ,x-3=0 x=0, y=0.
,x-3=0 x=0, y=0.
ЗАДАНИЕ 10
Решить дифференциальное уравнение, построить интегральные кривые, выделить на рисунке кривую, проходящую через точку М (0; -1), записать уравнение этой кривой.
10.1 (х + 4) •dy-(y- 2) •dх = 0
10.2 х -1) •dy- 2(y- 2) •dх = 0
10.3 dy- 3(х -1)2 •dх = 0
10.4 3(y+ 1) •dх - (1 + х) •dy= 0
10.5 dy- 2(х +1) •dх = 0
10.6 (y-1) •dy+ (х + 2) •dх = 0
10.7 y•dy- х •dх = 0
10.8 ctgх •dy+y•dх = 0
10.9 (y+ 3) •dx - (х - 2) •dy= 0
10.10y•dy+ 2 х •dx = 0
