Скалярное произведение векторов
О.Скалярное произведение двух векторов 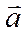 и
и 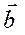 – число, равное произведению их модулей на
– число, равное произведению их модулей на 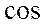 угла между ними.
угла между ними. 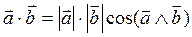
Св-ва:
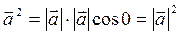
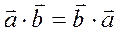
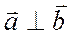 тогда и только тогда, когда
тогда и только тогда, когда 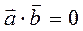
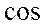 угла между векторами вычисляется по ф-ле:
угла между векторами вычисляется по ф-ле: 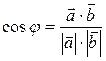
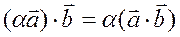
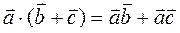
Т. Если векторы имеют координаты 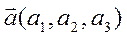 ;
; 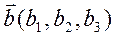 , тогда
, тогда 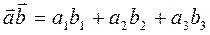
Правые и левые с-мы координат.
Три некомпланарных вектора 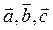 в указанном порядке наз-ют тройкой векторов.
в указанном порядке наз-ют тройкой векторов.
 Пусть
Пусть 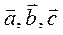 отложены из одной точки, будем смотреть из конца вектора
отложены из одной точки, будем смотреть из конца вектора 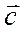 на плоскость, содержащую
на плоскость, содержащую 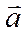 и
и 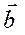 . Если кратчайший поворот от
. Если кратчайший поворот от 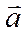 к
к 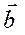 осуществляется против часовой стрелки, то тройка векторов
осуществляется против часовой стрелки, то тройка векторов 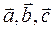 наз правой тройкой, если по часовой-то левой.
наз правой тройкой, если по часовой-то левой.
Векторное произведение векторов.
О. Векторным произведением 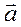 на
на 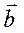 наз
наз 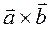 , к-рый удовлетворяет след. условиям:
, к-рый удовлетворяет след. условиям:
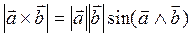
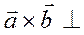 каждому из векторов
каждому из векторов 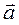 и
и 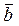
тройка векторов 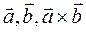
Св-ва:
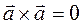
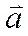 и
и 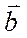 -коллинеарны только тогда, когда
-коллинеарны только тогда, когда 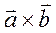 =0
=0
площадь параллелограмма, построенного на векторах 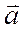 и
и 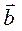 = модулю векторного произведения
= модулю векторного произведения 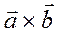
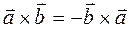
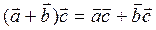
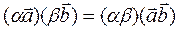
Т. Пусть 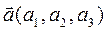 ,
, 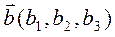 , тогда
, тогда 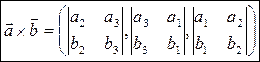
Разложим 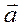 и
и 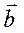 по базисным векторам
по базисным векторам 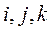
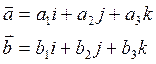
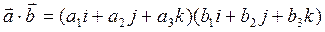 =
= 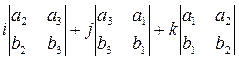
| x | i | j | k |
| i | 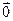 | 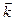 | 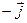 |
| j | 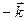 | 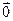 | 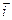 |
| k | 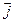 | 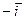 | 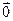 |
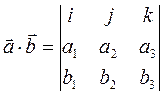
Смешанное произведение
Пусть даны 3 вектора 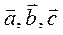 . Умножим
. Умножим 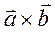 векторно, а полученный р-т скалярно на
векторно, а полученный р-т скалярно на 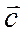 . В р-те получим число
. В р-те получим число 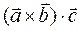 , называемое смешанным произведением векторов
, называемое смешанным произведением векторов 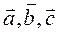 .
.
Смешанное произведение 3-х некомпланарных векторов 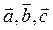 равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «+», если тройка
равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «+», если тройка 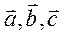 правая и со знаком «-« - если правая.
правая и со знаком «-« - если правая.
Следствие. 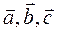 компланарны только тогда, когда их смешанное произведение =0.
компланарны только тогда, когда их смешанное произведение =0.
Т. Пусть 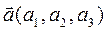 ,
, 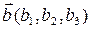 ,
, 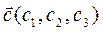 , тогда
, тогда 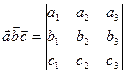
Вопрос №12. Плоскость в пространстве.
Ур-ние плоскости по точке и норм. вектору.
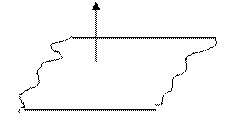 Пусть дана точка
Пусть дана точка 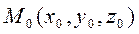 и
и 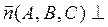 плоскости. Пусть
плоскости. Пусть 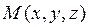 -произвольная точка плоскости. Рассм. вектор
-произвольная точка плоскости. Рассм. вектор 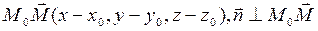
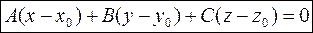 (1)
(1) 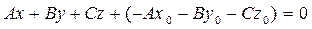 Þ
Þ 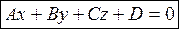 (2)
(2)
(1)-ур-ние по точке и нормальному вектору, (2)-общее ур-ние плоскости.
Частные случаи:1)если 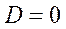 , то плоскость проходит через начало координат
, то плоскость проходит через начало координат
2)если 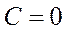 , тогда
, тогда 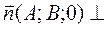 оси
оси 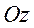 . След-но плоскость параллельна оси
. След-но плоскость параллельна оси 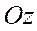
3) 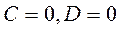 плоскость проходит через ось
плоскость проходит через ось 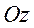
4) 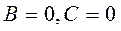 плоскость параллельна плоскости
плоскость параллельна плоскости 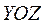
5) 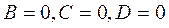 плоскость определяет координатную плоскость
плоскость определяет координатную плоскость 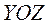
Ур-ние плоскости, проходящей через 3 данные точки
 Рассм. 3 точки, не лежащие на одной прямой
Рассм. 3 точки, не лежащие на одной прямой 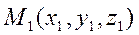 ,
, 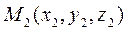 ,
, 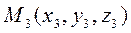 . Рассм. произвольную точку
. Рассм. произвольную точку 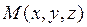 , лежащую в этой плоскости. Рассм.
, лежащую в этой плоскости. Рассм. 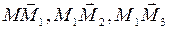 .
.
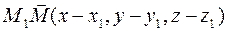 ,
, 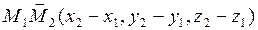 ,
, 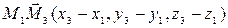
т.к. 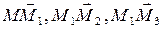 компланарны, то их смешанное произведение =0, т.е.
компланарны, то их смешанное произведение =0, т.е. 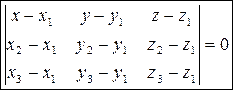 - ур-ние плоскости по 3 точкам.
- ур-ние плоскости по 3 точкам.
Взаимное расположение двух плоскостей.
Пусть даны 2 плоскости 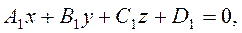
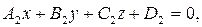 1-ая плоскость имеет
1-ая плоскость имеет 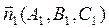 ,
, 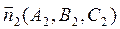 . Если плоскости параллельны, то
. Если плоскости параллельны, то 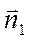 и
и 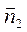 коллинеарны. Поэтому
коллинеарны. Поэтому 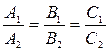 – условие параллельности плоскостей.
– условие параллельности плоскостей. 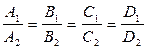 –условие совпадения плоскостей.Если условие параллельности не выполняется, то плоскости пересекаются. В частности ^ плоскостей равносильна ^ их нормальных векторов.
–условие совпадения плоскостей.Если условие параллельности не выполняется, то плоскости пересекаются. В частности ^ плоскостей равносильна ^ их нормальных векторов.
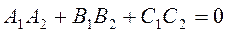 - условие перпендикулярности.
- условие перпендикулярности.
